Dopo avere imparato cosa sono le frazioni, cosa sono le frazioni equivalenti, come si fa a sommare tra loro frazioni con lo stesso denominatore e a sommare e sottrarre due frazioni con denominatore diverso, è arrivato il momento di fare un altro passo avanti. È arrivato il momento di capire come si eseguono l’ addizione e la sottrazione tra più frazioni. Non ti preoccupare niente di difficile, il procedimento è solo più lungo di quello visto quando si sommano due frazioni. Cominciamo subito con un esempio numerico.
Se non l’hai ancora fatto, iscriviti al mio canale Youtube.
Indice
Primo esempio
Supponiamo di voler eseguire la seguente addizione.
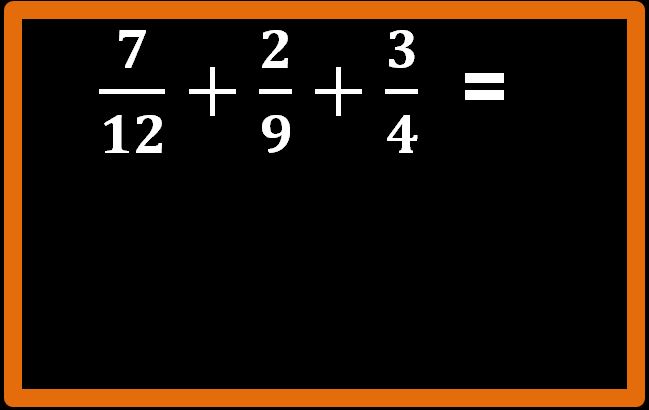
Il primo passaggio da fare è quello di trovare il minimo comune multiplo tra i denominatori. (Ti ricordo che in una frazione il denominatore è tutto quello che si trova sotto la linea di frazione).
Se non ti ricordi come si trova il minimo comune multiplo (m.c.m.) puoi dare un’ occhiata al mio articolo calcolo del minimo comune multiplo in modo semplice.
Nel nostro esempio i denominatori sono: 12, 9, e 4. Per trovare l’m.c.m. dobbiamo scomporli in fattori primi e poi scegliere i fattori appropriati.
Se non ti ricordi come si fa a scomporre in fattori primi sarebbe il caso di andarlo a ripassare, potresti farlo leggendo il mio articolo che trovi a questo link.
Come avrai già capito, prima di poter addizionare tra loro frazioni con denominatore diverso è necessario conoscere alcuni concetti (scomposizione in fattori primi e minimo comune multiplo). È meglio impiegare un po’ di tempo per ripassare o studiare questi argomenti prima di passare alla somma tra frazioni.
Passaggio 1
Detto questo, andiamo avanti con l’esercizio per capire come si eseguono l’addizione e la sottrazione tra frazioni.
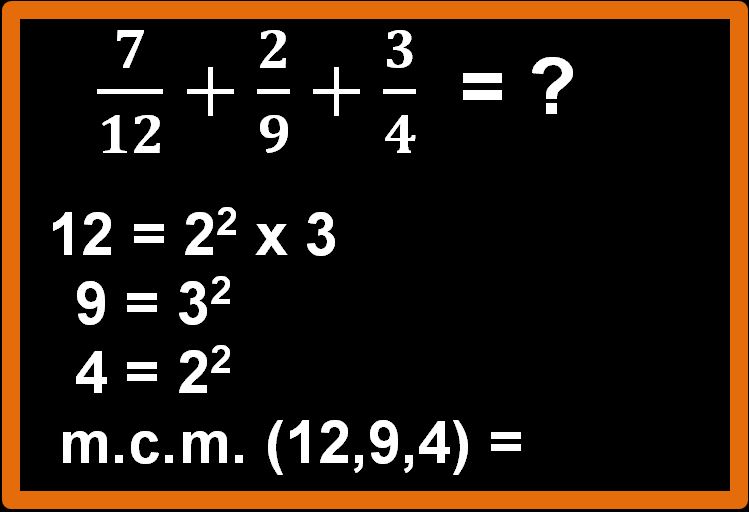
Abbiamo scomposto i denominatori in fattori primi. Ora dobbiamo scegliere i fattori che ci permetteranno di determinare l’ m.c.m.. Ti ricordo che la regola dice:
“Vanno scelti i fattori comuni e non comuni presi una sola volta con l’esponente maggiore.”
Per cui noi sceglieremo 32 e 22 .
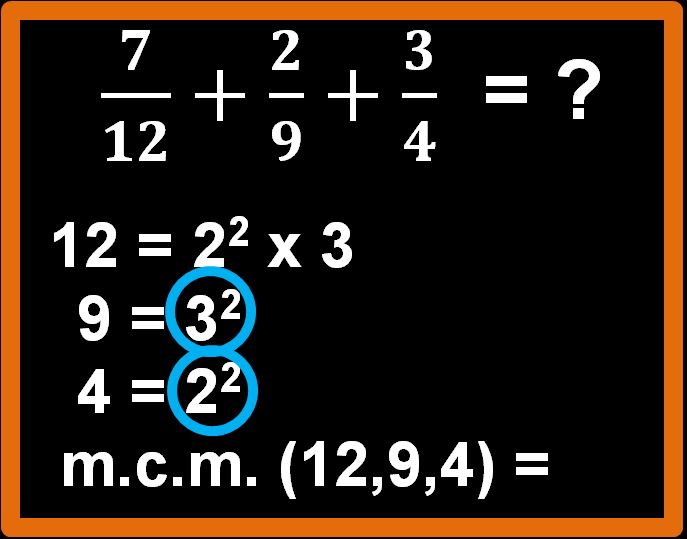
Andiamo adesso a moltiplicare 22 per 32 e otterremo il nostro m.c.m..
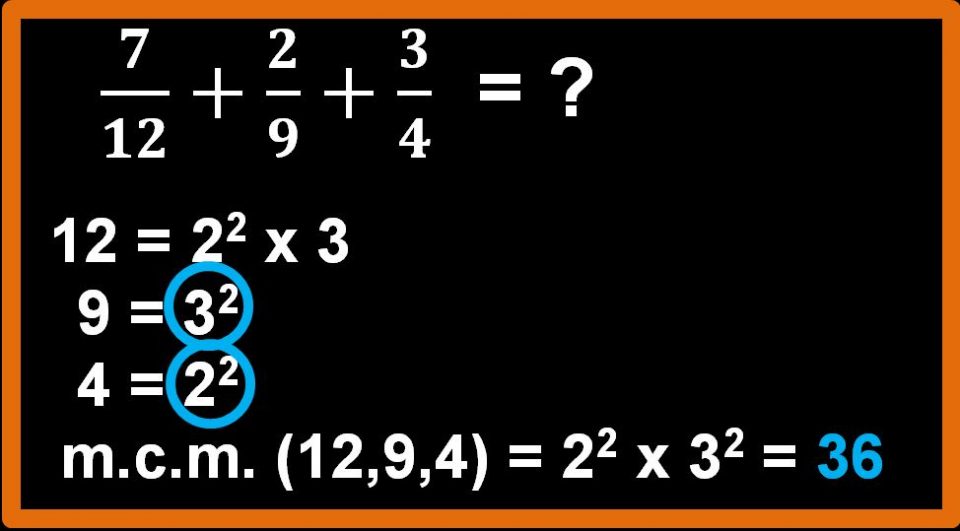
Passaggio 2
Una volta trovato l’m.c.m., tracciamo una lunga linea di frazione e mettiamo l’m.c.m. come denominatore.
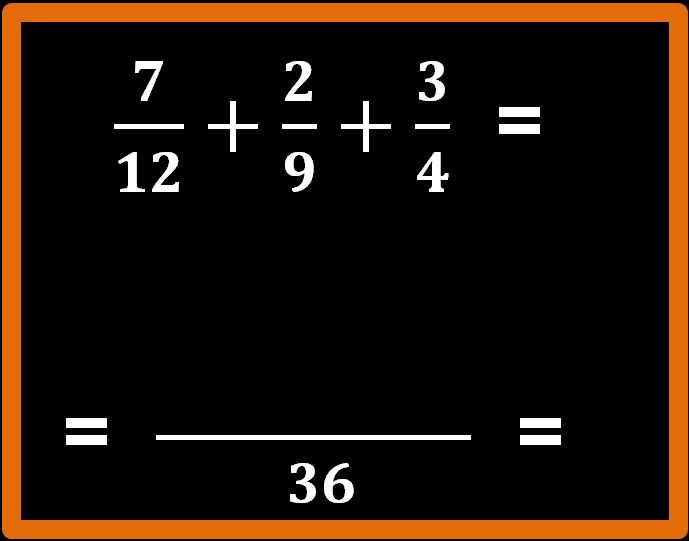
Ora dobbiamo seguire lo stesso procedimento che abbiamo visto quando abbiamo sommato due frazioni.
Lo ripetiamo (è più difficile spiegarlo che applicarlo).
Per eseguire l’ addizione (o la sottrazione) tra frazioni si divide l’m.c.m. (36) per il denominatore della prima frazione (12) e si moltiplica il risultato per il numeratore (7). Le operazioni che andremo a fare sono quindi queste:
36 : 12 = 3; 3 · 7 = 21
Andiamo a scrivere 21 al numeratore. Poi riscriviamo il segno ” + ” dell’addizione.
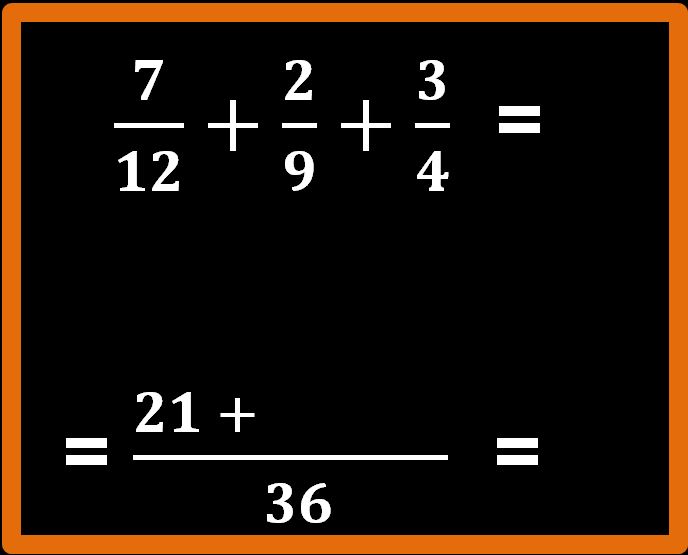
Ripetiamo lo stesso procedmento per la seconda frazione. Le operazioni che andremo a eseguire sono:
36 : 9 = 4; 4 · 2 = 8
E scriviamo anche il numero 8 al numeratore e riscriviamo il segno ” + “.
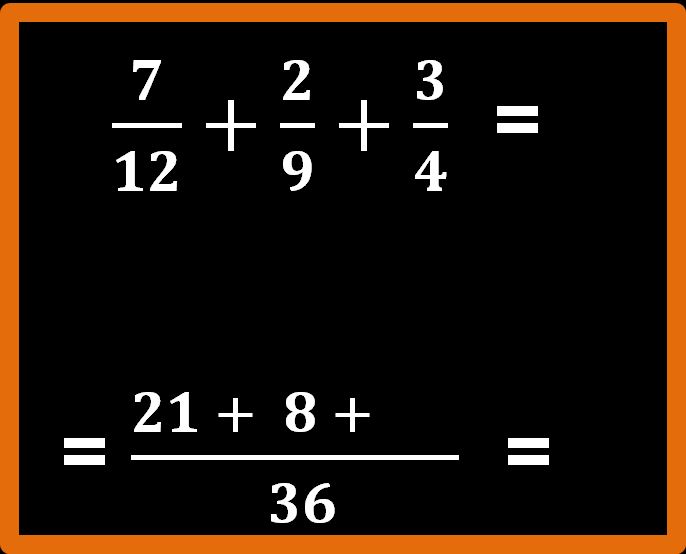
Non ci rimane che ripetere il procedimento anche con la terza e ultima frazione.
36 : 4 = 9; 9 · 3 = 27
Il 27 sarà l’ultimo addendo della nostra addizione e lo scriviamo al numeratore.
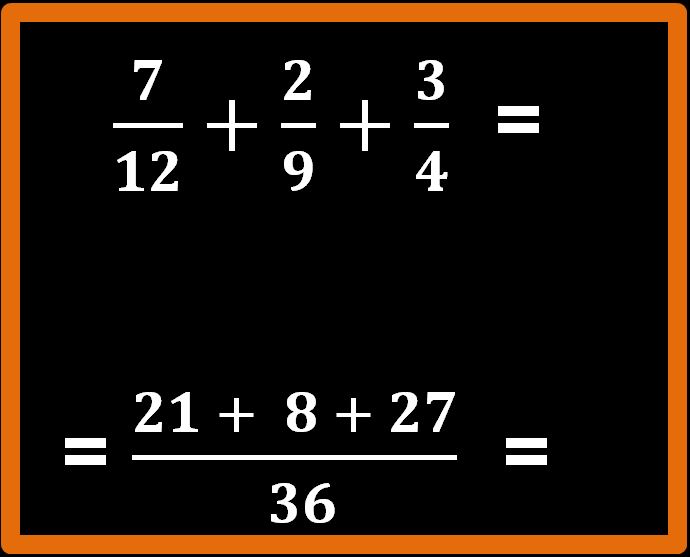
Passaggio 3
Fantastico. Adesso dobbiamo addizionare i numeri che abbiamo ottenuto al numeratore. L’operazione che dobbiamo fare è :
21 + 8 + 27 = 56

Il risultato che abbiamo trovato è cinquantasei trentaseiesimi. Attenzione non abbiamo ancora finito. Come ti avrà di certo detto la tua prof (o il tuo prof) quando è possibile, si deve sempre ridurre una frazione ai minimi termini.
Ridurre ai minimi termini vuol dire dividere sia il numeratore che il denominatore per lo stesso numero, in modo tale da avere una frazione equivalente (che ha lo stesso valore) ma in cui compaiono numeri più piccoli.
Possiamo dividere sia il 56 che il 36 per 2.
56 : 2 = 28; 36 : 2 = 18.
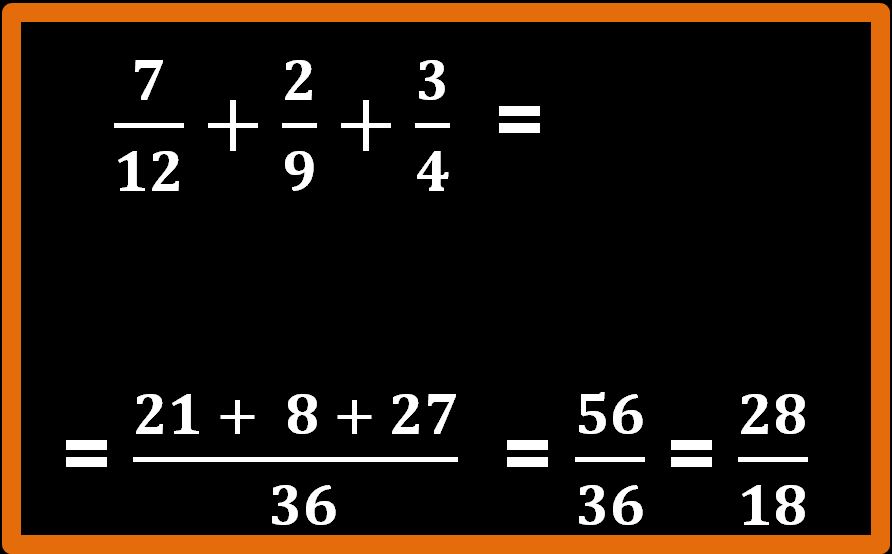
Non ci siamo ancora, non abbiamo ancora ridotto ai minimi termini. Infatti possiamo ancora dividere numeratore e denominatore per 2.
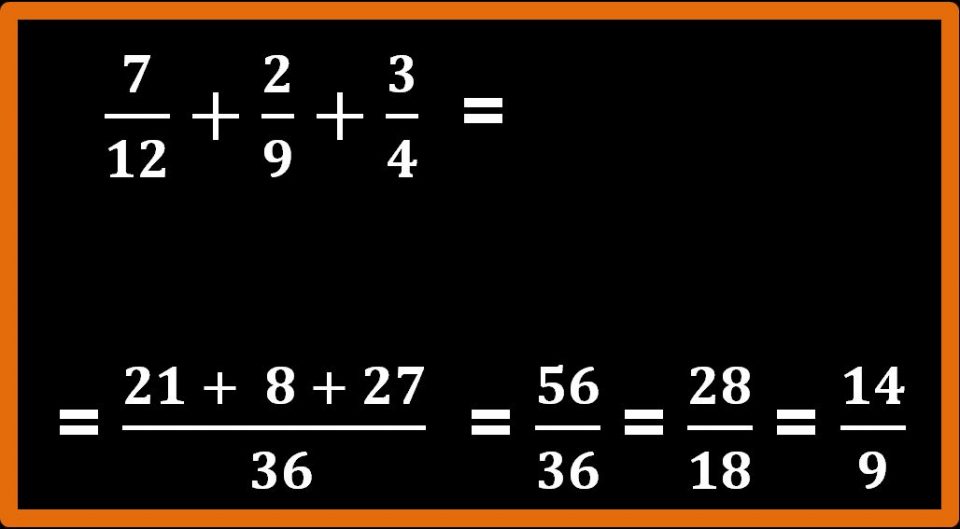
Adesso sì che abbiamo finito. La frazione quattordici noni è una frazione ridotta ai minimi termini, infatti non è più possibile dividere il numeratore e il denominatore per lo stesso numero e ottenere un numero naturale (senza virgola). Il risultato che stavamo cercando è 14 su 9.
In tutta la matematica pratica, a qualsiasi livello, da una classe di prima media ai laboratori della NASA è sempre consigliabile lavorare con numeri piccoli (quando è possibile), perché sono più facili da maneggiare (motivo per cui è stata inventata la notazione esponenziale.
Secondo esempio
Facciamo un altro esempio in cui abbiamo un’addizione e una sottrazione. Niente paura il procedimento è identico, è sufficiente fare attenzione ai segni.
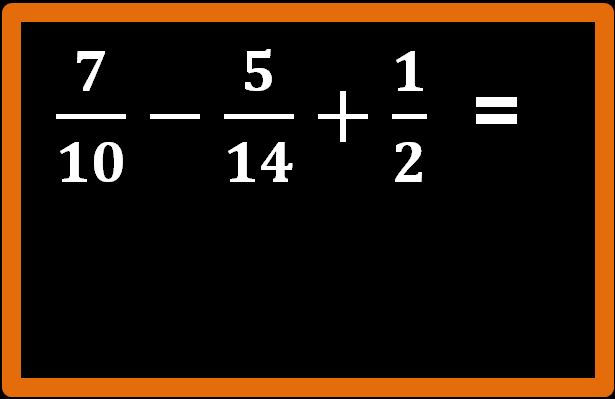
Come primo passaggio troviamo il minimo comune multiplo tra i denominatori e per fare questo dobbiamo prima scomporli in fattori primi.
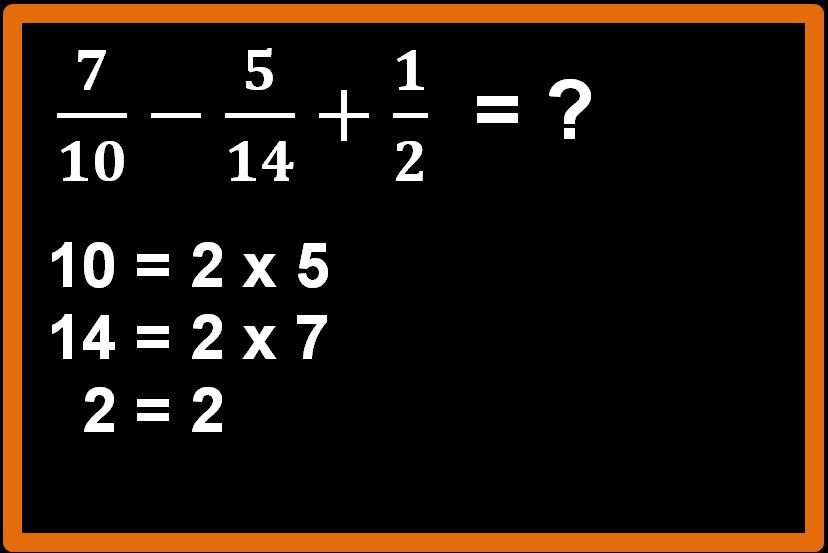
Una volta scomposti in fattori primi i denominatori, calcoliamo l’m.c.m..
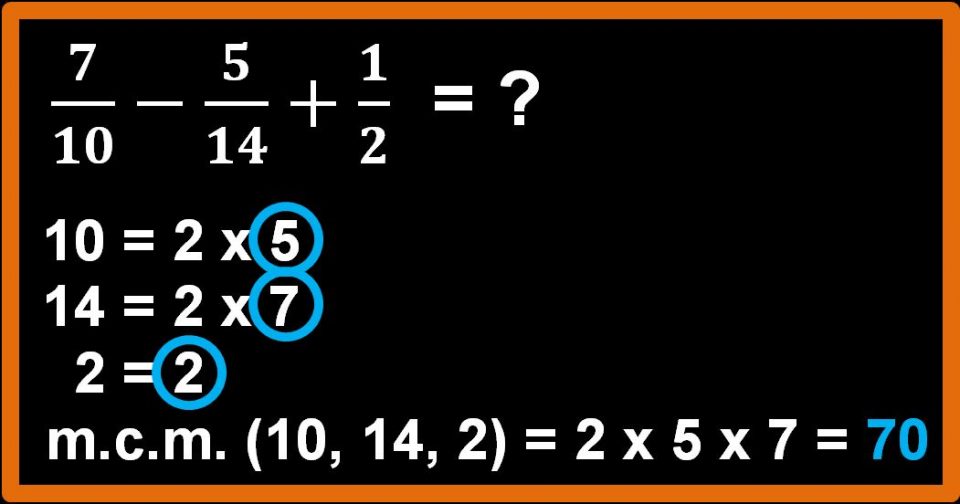
Trovato l’m.c.m., tracciamo una linea di frazione sufficientemente lunga e mettiamo 70 al denominatore.
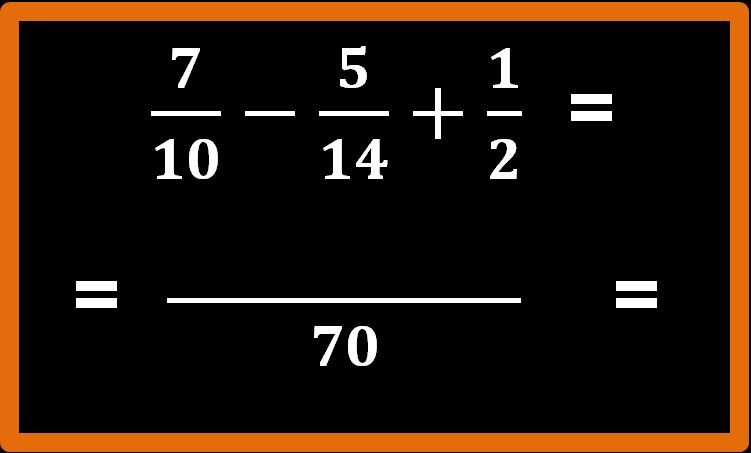
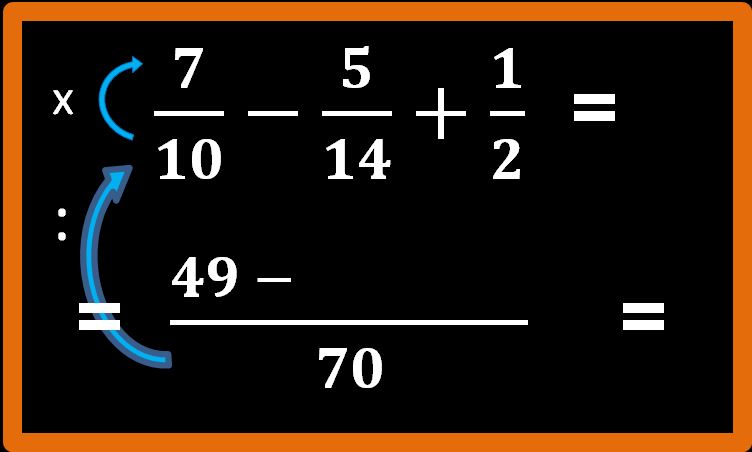
Procediamo come sempre e cioè:
70 : 10 = 7; 7 · 7 = 49
Facciamo attenzione al segno che si trova dopo la prima frazione. Se c’è meno, noi nella frazione di sotto dobbiamo riportare meno.
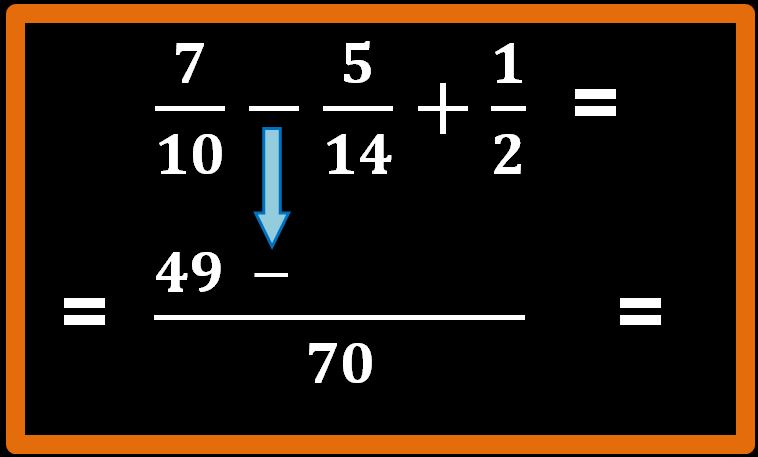
Poi passiamo a effettuare i calcoli per la seconda frazione:
70 : 14 = 5; 5 · 5 = 25
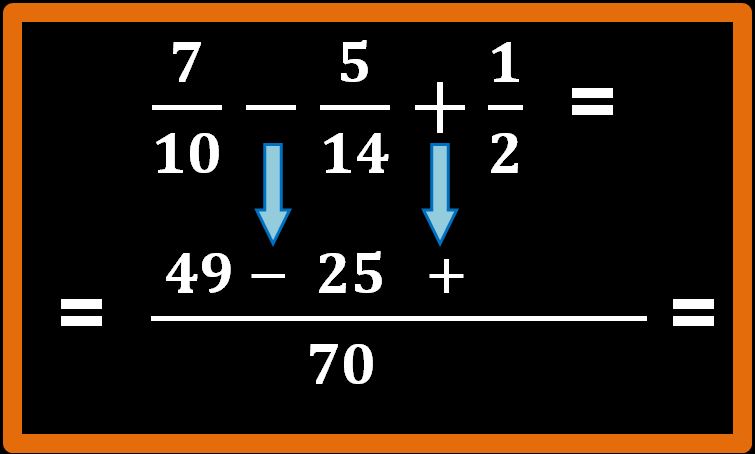
Ci rimangono i calcoli relativi alla terza frazione:
70 : 2 = 35; 35 · 1 = 35
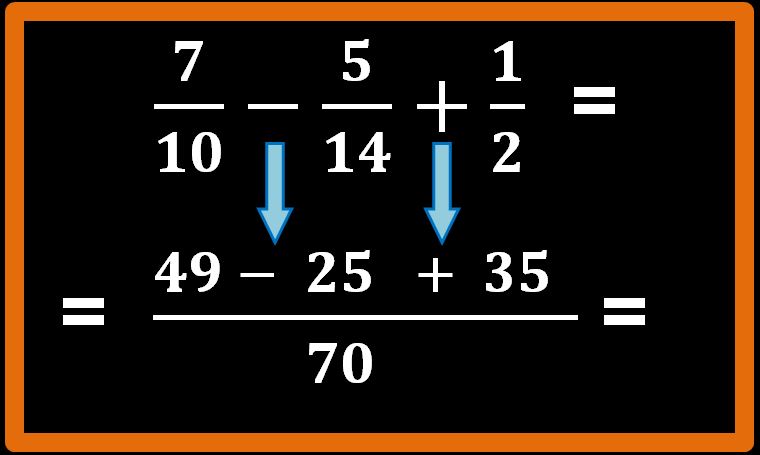
Perfetto, fatto ciò, dobbiamo eseguire le operazioni presenti al numeratore: una sottrazione e una addizione.
49 – 25 + 35 = 51
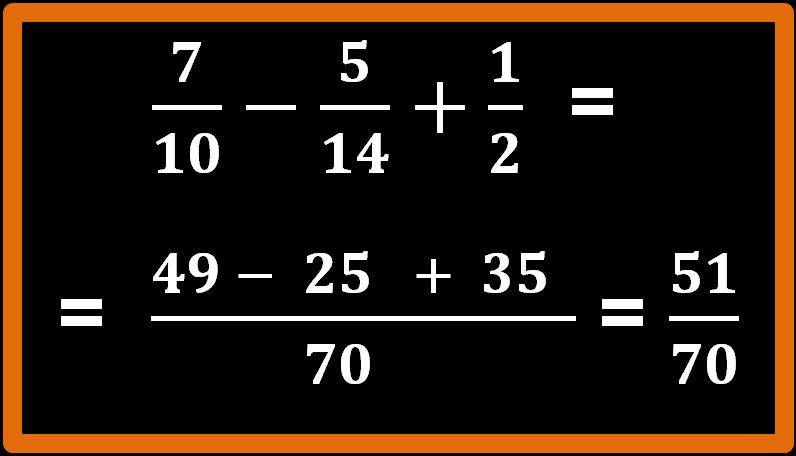
Prima di poter dire che abbiamo concluso dobbiamo osservare con attenzione la frazione 51 su 70. Dobbiamo cercare di capire se è una frazione ridotta ai minimi termini oppure no. In altre parole dobbiamo cercare di capire se i numeri 51 e 70 hanno dei divisori comuni.
51 è divisibile per 3, ma 70 non è divisibile per 3.
70 è divisibile per 5, per 10, per 7 e per 2, ma 51 non è divisibile per nessuno di questi numeri. (Se non ti ricordi i criteri di divisibilità puoi andare a dare una lettura al mio articolo).
Possiamo allora dire che la frazione cinquantuno settantesimi è ridotta ai minimi termini.
Quindi 51 su 70 è il risultato che stavamo cercando. Esercizio concluso.
Terzo esempio
Continuiamo con un altro esercizio di addizione e sottrazione tra frazioni. Vogliamo calcolare quanto fa sette quindicesimi più cinque sesti meno tre ottavi più un quarto.
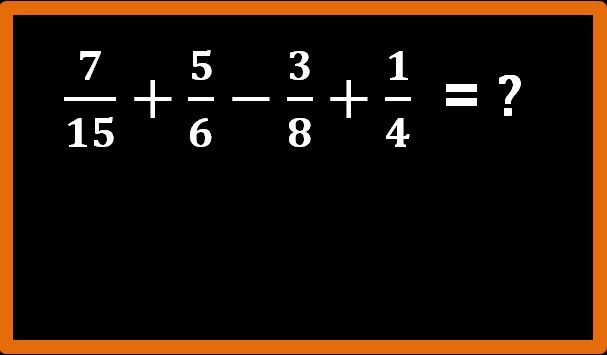
La prima cosa da fare è trovare l’m.c.m. tra i denominatori. Ma per trovare l’m.c.m. dobbiamo prima scomporre in fattori primi i denominatori. Procediamo.
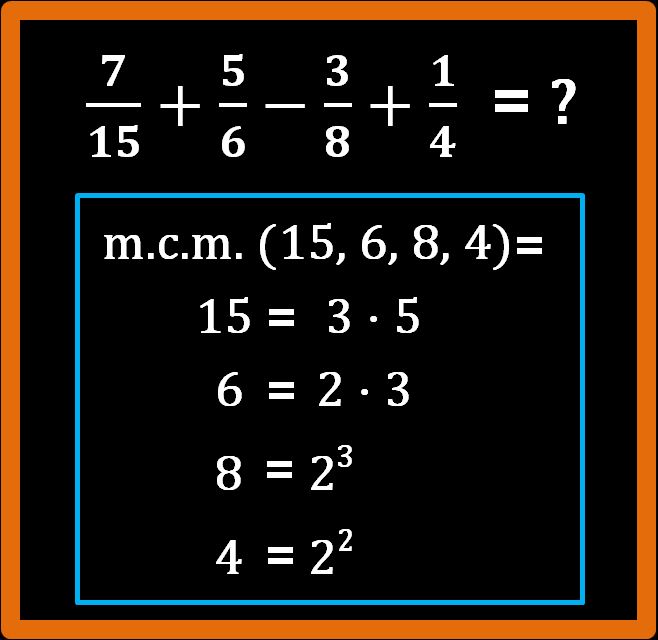
Scegliamo adesso i fattori che ci permetteranno di calcolare in modo corretto l’m.c.m.. Ricordiamo la regola: “vanno scelti i fattori comuni e non comuni con il maggiore esponente presi una sola volta”.
Partiamo dal fattore 2. È presente nella scompsizione:
- del 6, con esponente 1; (ti ricordo che 2 = 21);
- dell’8, con esponente 3; (23);
- del 4, con esponente 2; (22 ).
Noi ne dobbiamo scegliere solo uno. Dobbiamo scegliere quello con l’esponente maggiore.
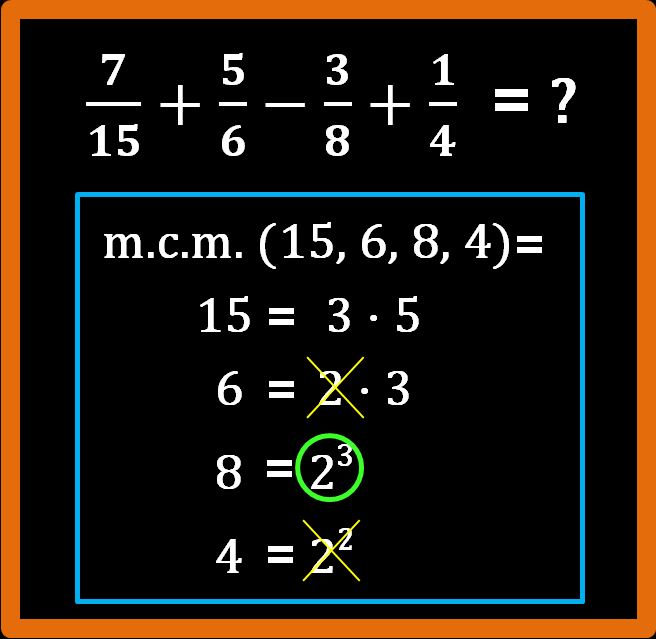
Ora passiamo al fattore 3. Compare nella scomposizione del 15 e del 6 con lo stesso esponente. Noi ne dobbiamo scegliere solo uno e dobbiamo scartare l’altro, perché la regola dice “presi una sola volta”.

È corretto anche nel modo che vedi sotto:

Invece sceglierli tutti e due è sbagliato.

L’ultimo che dobbiamo scegliere è il 5.

Ora che abbiamo scelto i fattori, calcoliamo l’m.c.m.

Il minimo comune multiplo, diventa il denominatore delle nostre frazioni.
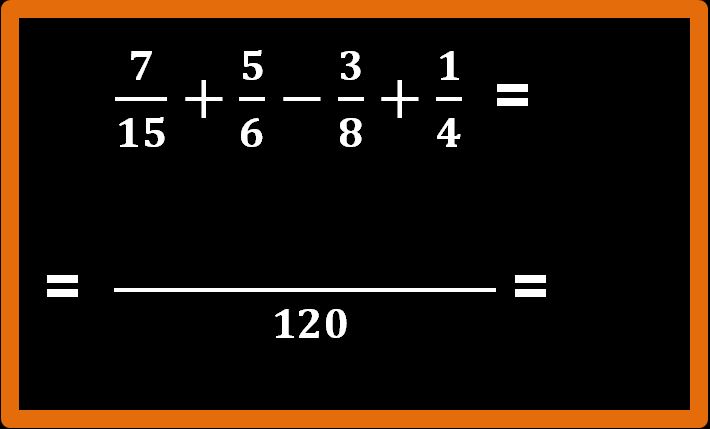
Le operazioni che dobbiamo eseguire sono:
120 : 15 = 8 e poi 8 · 7 = 56
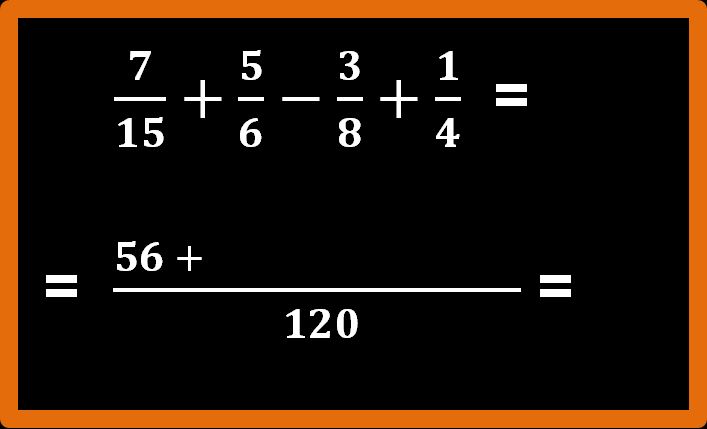
Ripetiamo lo stesso procedimento anche per le altre frazioni, facendo attenzione ai segni di più e meno.
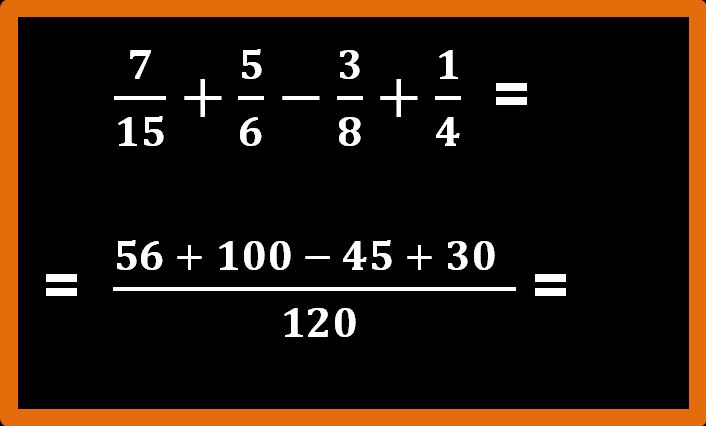
Eseguiamo le addizioni e la sottrazione presenti al numeratore.

Otteniamo la frazione 141 fratto 120. Non abbiamo ancora finito, infatti dobbiamo ridurre ai minimi termini. Possiamo dividere sia il numeratore, sia il denominatore per 3. In altre parole usiamo come fattore di riduzione 3.
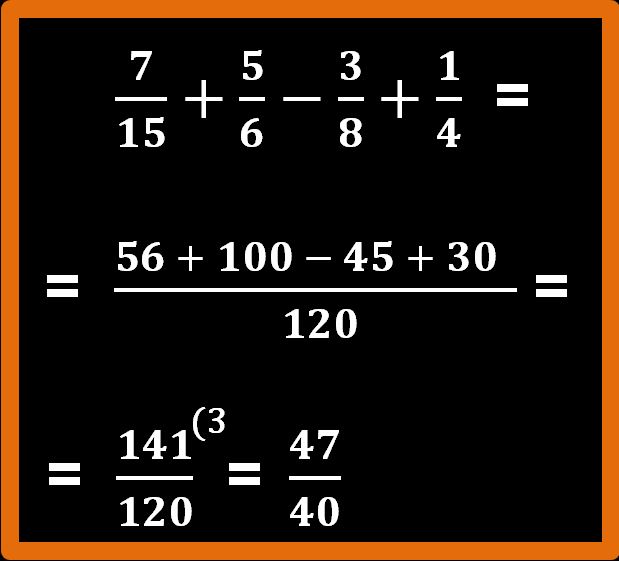
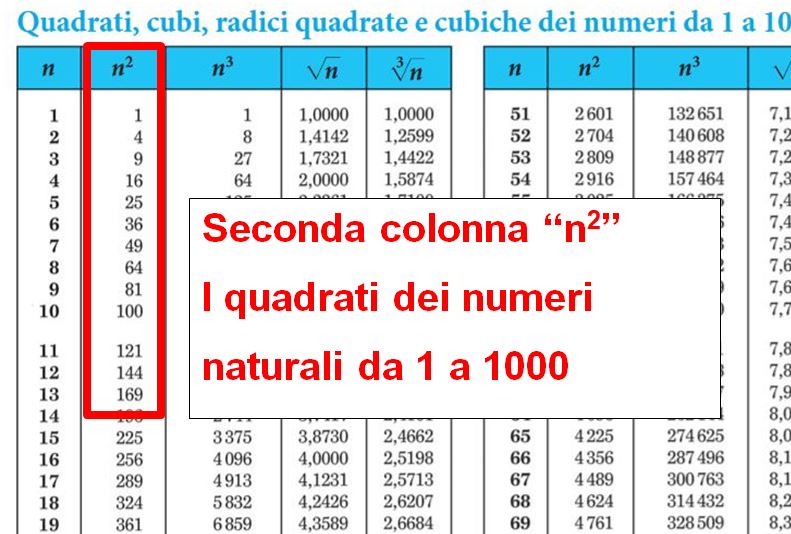
Fantastico. Siamo arrivati alla frazione quarantasette quarantesimi. Se andiamo a consultare le tavole numeriche a pagina 13, ci accorgiamo che il numero 47 è un numero primo. Per cui la frazione è ridotta ai minimi termini. Esercizio concluso.

Altri esercizi
Se vuoi vedere qualche altro esercizio svolto che ti spieghi come si esegue l’ addizione e la sottrazione tra frazioni puoi guardare in questa pagina. Se per esempio ti stai chiedendo come si esegue la differenza
allora in questo mio articolo troverai proprio quello che stai cercando. Buon lavoro
Esercizi in pdf
Adesso possiedi gli strumenti necessari per eseguire qualsiasi addizione o sottrazione tra frazioni. Se vuoi puoi allenarti con gli esercizi che trovi nel file pdf sotto. La vora con calma e non avere premura di finire. E non ti preoccupare se ti capita di ottenere un m.c.m. molto grande, a volte succede. Buon lavoro.
A questo link trovi le tavole numeriche che puoi consultare o scaricare come file pdf fornite dalla Casa Editrice Zanichelli.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato a tutti quei lettori che segnaleranno eventuali errori presenti nell’articolo.