Se sei finito in questa pagina è perchè hai sentito parlare dell’algoritmo di Euclide per il calcolo del M.C.D., ma non sai di cosa si tratta. Niente paura, non è niente di difficile, con 5 minuti di impegno riuscirai a capire come funziona questo antico procedimento per il calcolo del massimo comune divisore.
indice
Un po’ di storia
Prima di passare ai numeri, un po’ di storia della matematica. Le prime tracce scritte di questo procedimento si trovano negli Elementi di Euclide. Euclide era un grande matematico nato in Grecia circa 2200 anni fa (all’epoca dei bisnonni dei bisnonni dei bisnonni dei tuoi nonni) e scrisse un libro che oggi è al secondo posto per vendite a livello mondiale (in alcune classifiche appare al terzo posto, ma per un libro scritto più di 2000 anni fa e che parla di geometria è un ottimo risultato).

La parola algoritmo significa semplicemente procedimento, deriva dall’arabo al-Khuwārizmī, che vuol dire originario della Corasmia, la regione da cui proveniva il grande matemaitico arabo Muḥammad ibn Mūsa. (Anche la parola algebra deriva da una parola araba: al-gabr, che vuol dire trasporto.)
Se vuoi ripassare il concetto di massimo comune divisore puoi leggere questo mio articolo. Se invece vuoi andare a leggere come si calcola i M.C.D. con il metodo della scomposizione in fattori primi, puoi leggere questo articolo.
esempio 1
Passiamo all’algoritmo di Euclide per il calcolo del massimo comune divisore. Supponiamo di dover trovare il massimo comune divisore tra 15 e 6, si scrive così:
M.C.D. (15, 6) =
La cosa positiva di questo procedimento è che non è necessario sapere come si scompongono i numeri in fattori primi, la cosa negativa è che devi sapere eseguire una divisione in colonna. (La scomposizione in fattori primi ti servirà comunque quando dovrai calcolare il minimo comune multiplo, quindi sarebbe meglio saperla eseguire.)
La prima cosa da fare è dividere 15 per 6. Scriviamo la divisione.

Solo per essere sicuri di ricordarci come si chiamano i termini della divisione, ripassiamoli: 15 è il dividendo, invece 6 è il divisore.

Benissimo, adesso procediamo alla divisione come ci hanno insegnao alle elementari. Il 6 nel 15 ci sta due volte. E scriviamo il numero 2 sotto il 6.

Adesso dobbiamo moltiplicare il 2 per il 6.
2 · 6 = 12
Dopo di che dobbiamo sottrarre 15 – 12 e scrivere il risultato della sottrazione sotto il 15. È più difficile scriverlo a parole che farlo con i numeri.
Benissimo, scriviamo la divisione che abbiamo effettuato. Abbiamo trovato il quoziente e il resto.
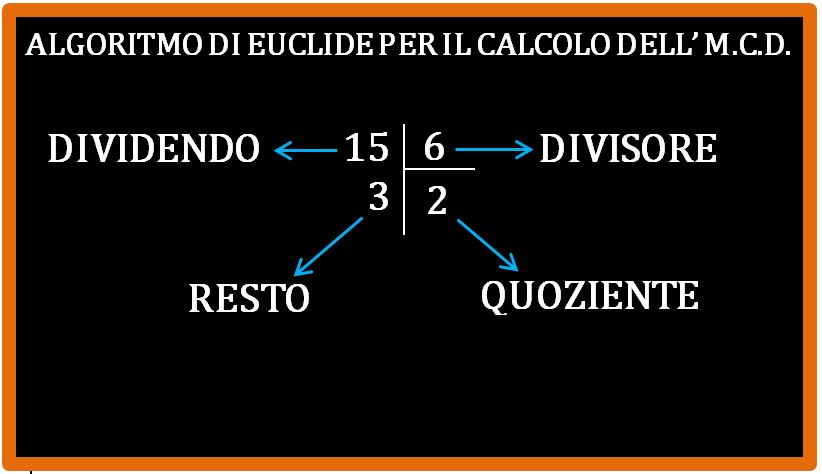
Fantastico. Il nostro scopo è arrivare ad avere una divisione con resto zero. Ora si procede nel modo seguente: il divisore diventa il dividendo e il resto diventa il divisore. Facciamolo con i numeri che è più semplice.
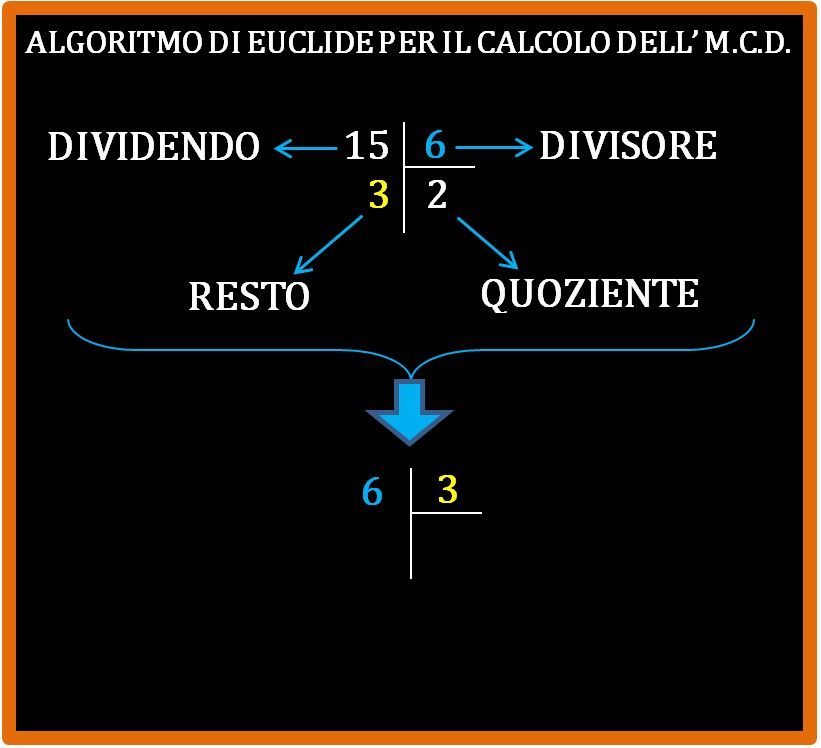
Bene. Eseguiamo la divisione e vediamo cosa otteniamo.
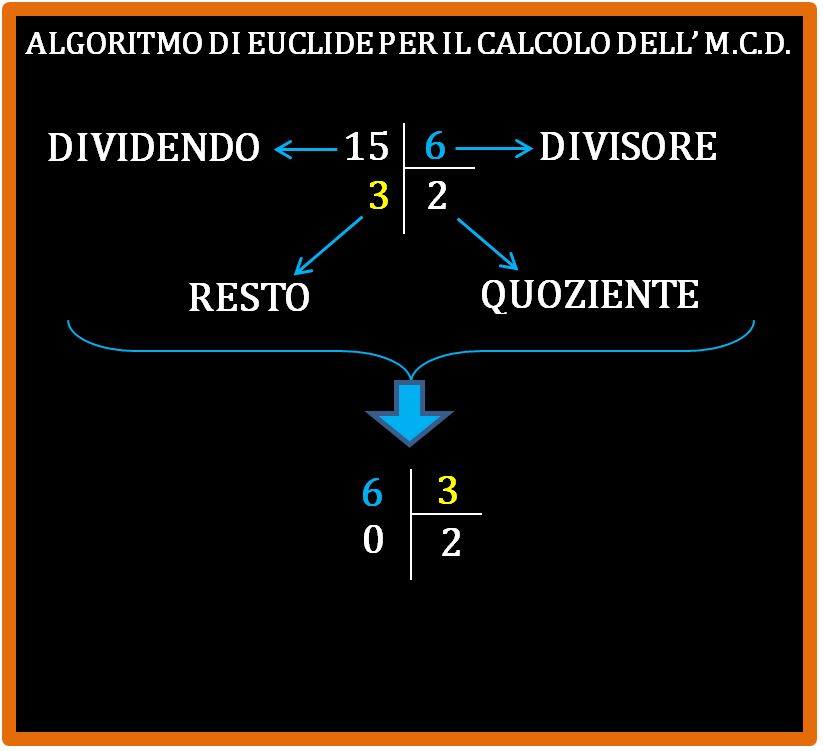
Fantastico. Abbiamo ottenuto una divisione con resto zero. Era quello che volevamo. Il divisore di questa divisione sarà il nostro massimo comune divisore.
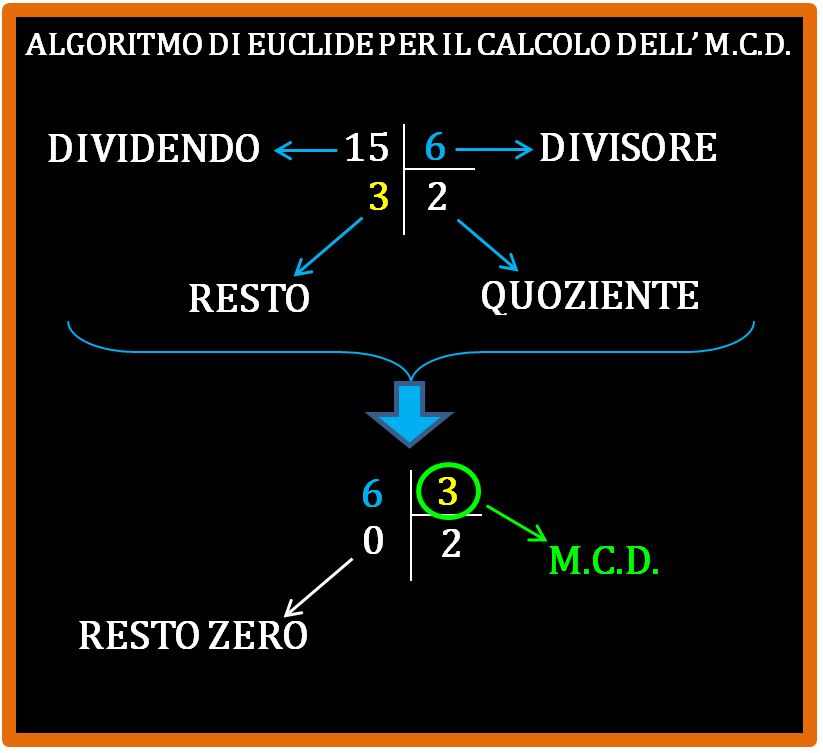
Il risultato che stavamo cercando è 3:
M.C.D. (15, 6) = 3
Esercizio concluso.
esempio 2
Facciamo un altro esempio per prendere più familiarità con l’algoritmo di Euclide per il calcolo dell’M.C.D.. Calcoliamo il massimo comune divisore tra 10 e 16.
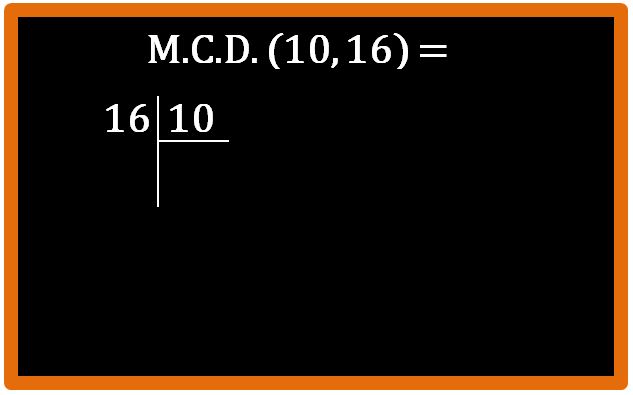
Eseguiamo la divisione.

Abbiamo ottenuto un resto diverso da zero, quindi dobbiamo andare avanti. 10 sarà il nostro dividendo e 6 il divisore.
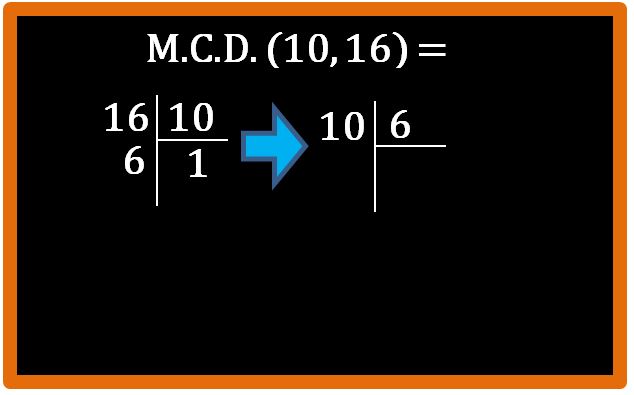
Eseguiamo la nostra divisione. Ti ricordo che il nostro scopo è trovare una divisione con resto zero.
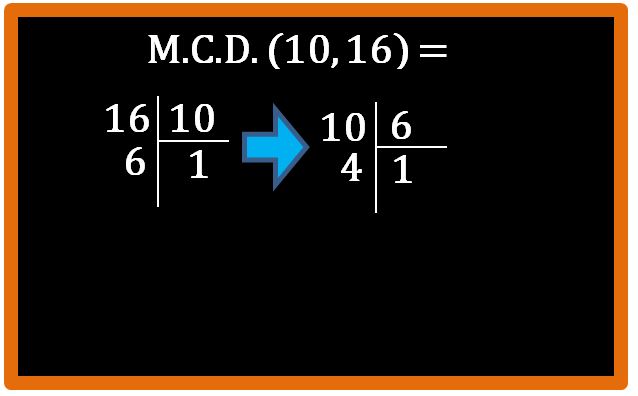
Dobbiamo andare ancora avanti in questo modo fino a quando non otteniamo una divisione con resto zero. Il divisore diventa dividendo e il resto diventa divisore.
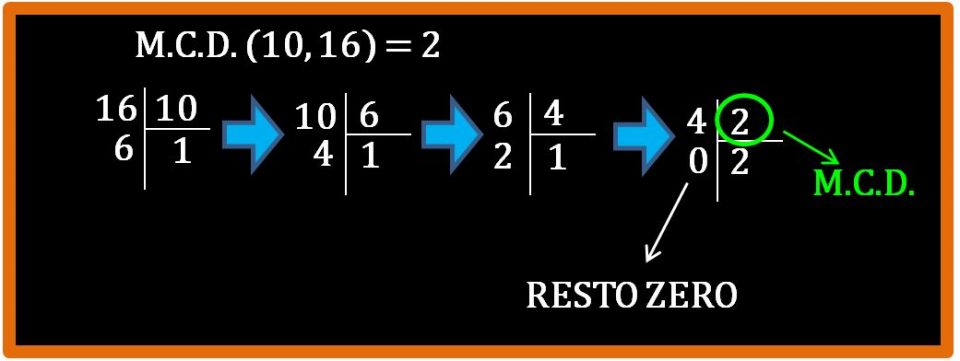
Benissimo, nell’ultima divisione il resto è zero. Il divisore della divisione sarà il massimo comune divisore che stavamo cercando.
Esercizio concluso.
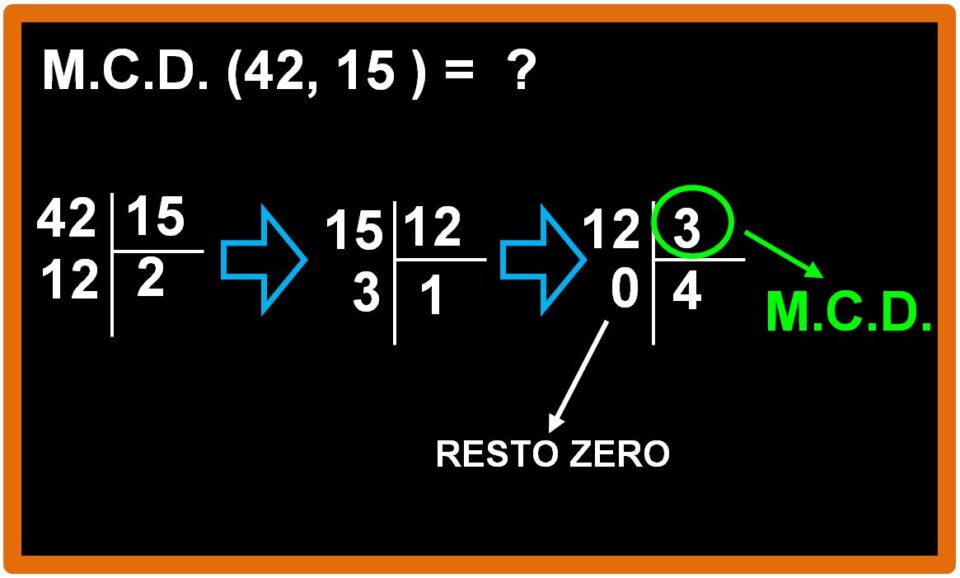
esempio 3
Ancora un altro esempio dell’applicazione dell’algoritmo di Euclide per il calcolo del massimo comune divisore.
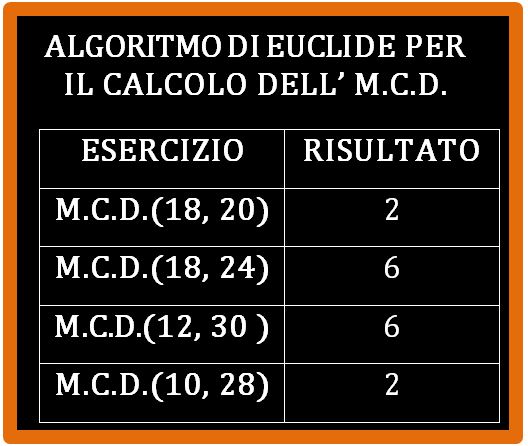
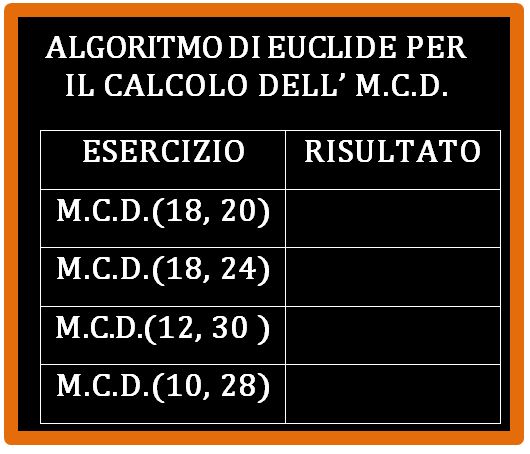
esercizi
Adesso prova da solo. Ti consiglio di prendere carta e penna e provare a eseguire gli esercizi da solo. Non ti preoccupare se sbagli, nessuno ti rimprovererà. Sbagliare è normale. Alla fine della pagina trovi i risultati che ti servono per capire se hai fatto bene.
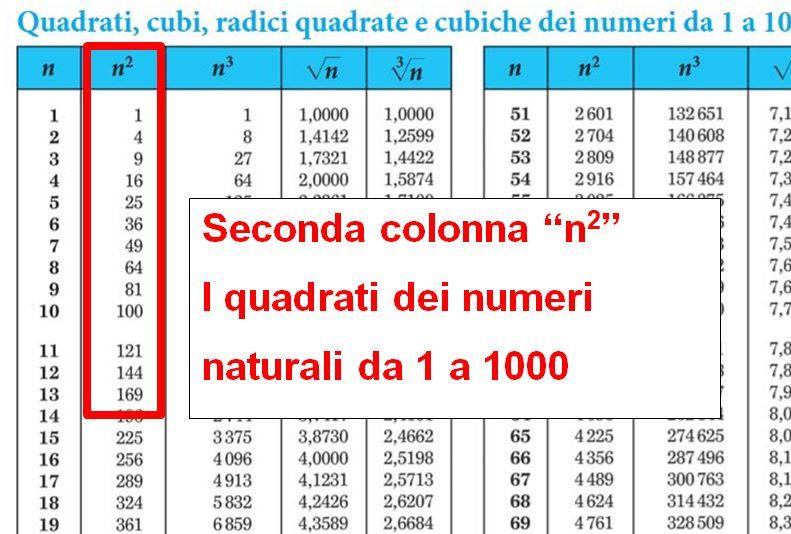
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche in formato pdf, per averle sempre a disposizione sul tuo pc anche quando sei off-line.
Se hai dubbi o vuoi segnalare un errore, puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
risultati