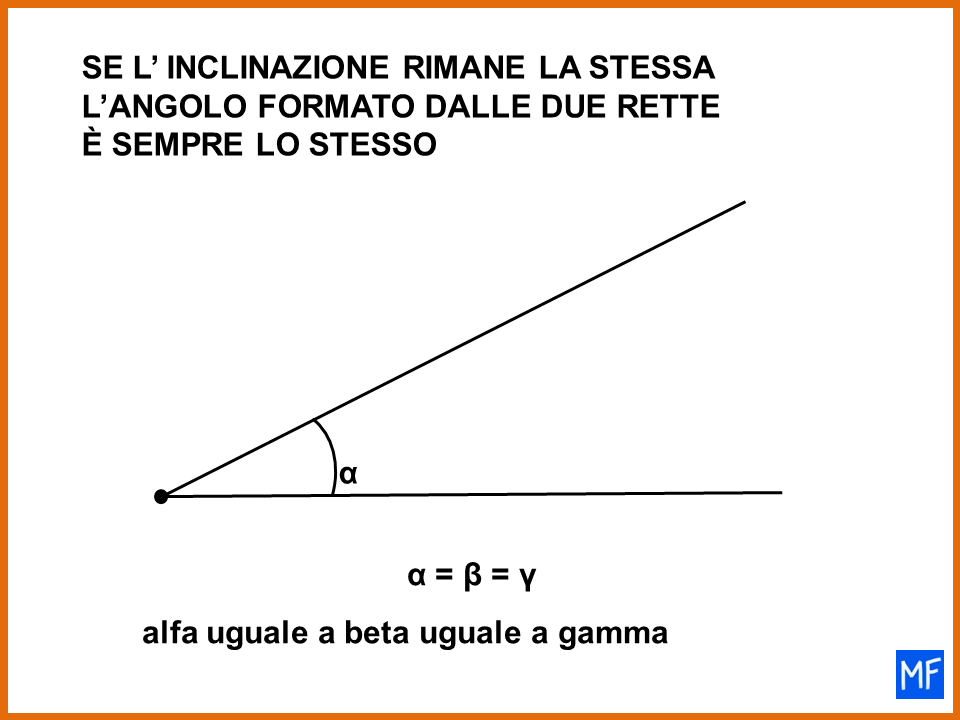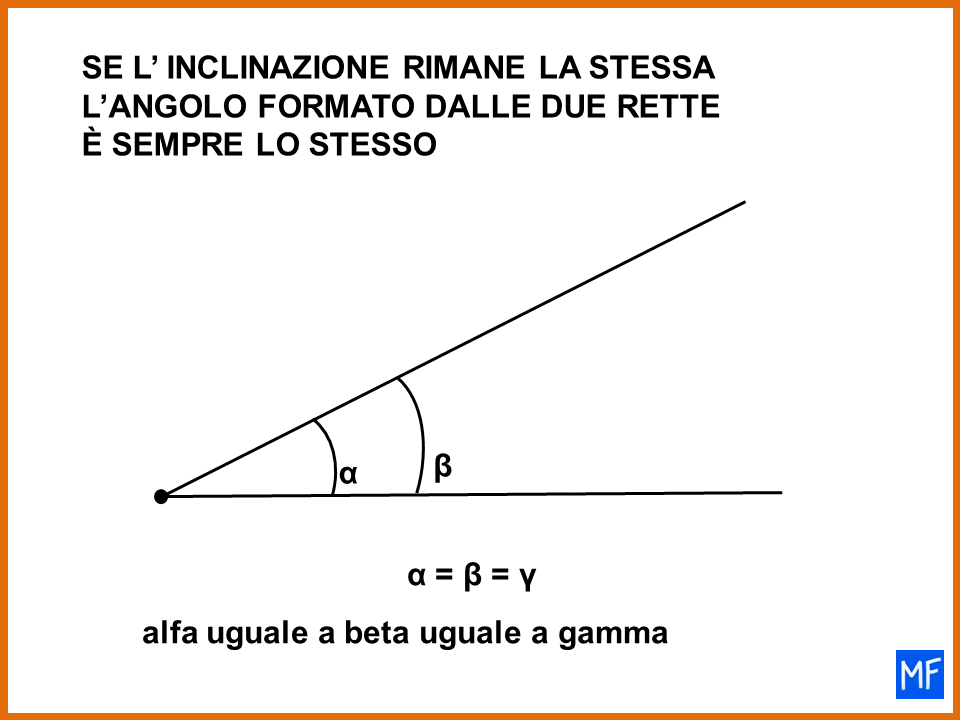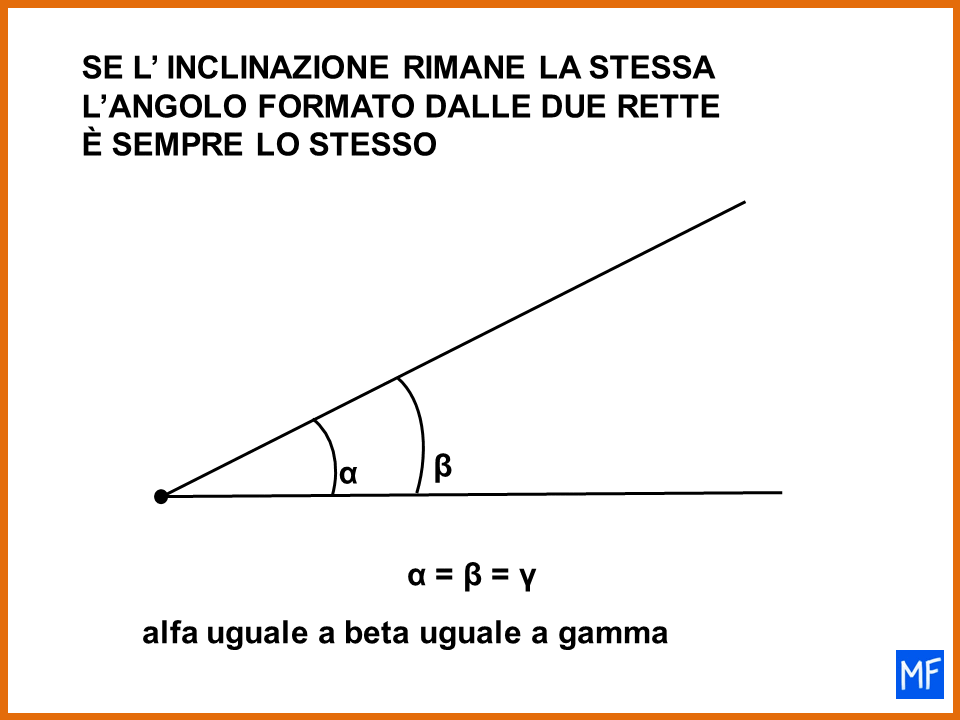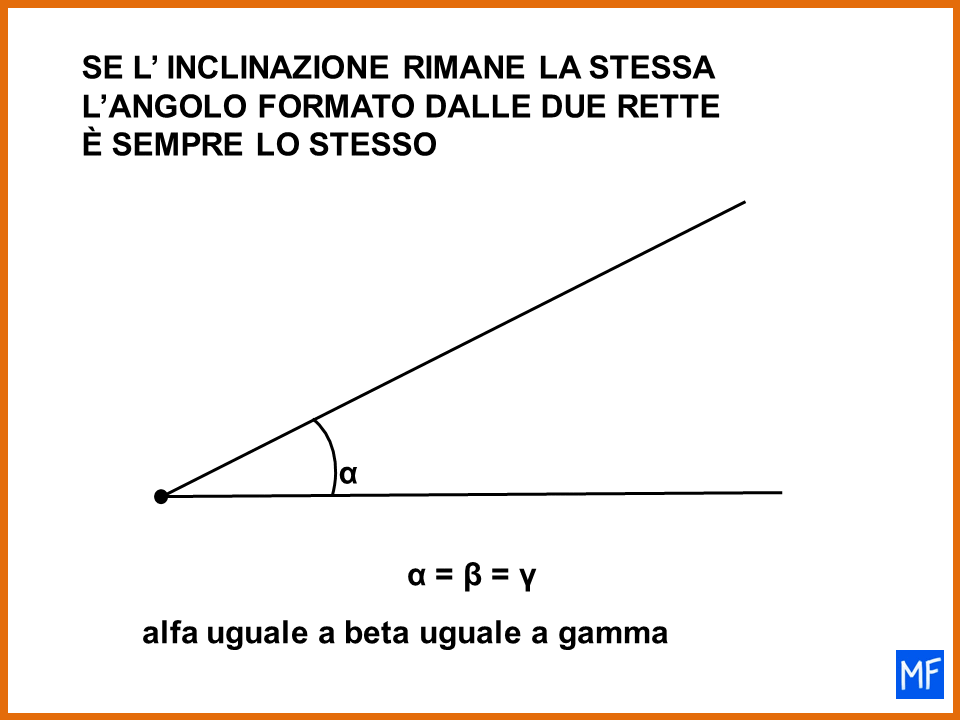
La geometria spesso risulta più complicata della matematica e il concetto di angolo è uno di quelli che crea più confusione. Non preoccuparti, non è colpa tua, è una situazione comune. Con 5 minuti di impegno capirai cosa sono gli angoli retti e le rette perpendicolari.
La confusione sul concetto di angolo forse nasce perchè in italiano la parola angolo è usata per indicare molte cose (angolo di un mobile, angolo cottura, angolo di paradiso, ecc). Ma anche i libri di geometria a volte sono poco precisi quando si parla di angolo. La cosa migliore da fare è andare con calma, partire con le cose facili e cercare di capire per il momento, quali sono gli angoli retti e le rette perpendicolari.
Indice
- Angolo retto
- Il goniometro
- Disegnare un angolo retto
- Semirette perpendicolari
- Segmenti perpendicolari
- Rette perpendicolari
- Esercizi in pdf
Angolo retto
Per capire quali sono gli angoli retti e le rette perpendicolari prova a guardare il tuo banco o il tavolo su cui fai colazione o la scrivania su cui studi. Quasi sicuramente i bordi del tavolo formeranno un angolo retto. Il modo più semplice per verificarlo è usare una delle tue squadre, come quella che vedi nell’immagine sotto. Forse la tua sarà di colore celeste, ma poco importa. In tutte le squadrette come quella che vedi sotto, il bordo più corto e il bordo in cui sono scritti i numeri formano un angolo retto.

Guarda l’immagine animata e prova anche tu.

Appoggia la squadra sul tavolo e sposta la parte con i numeri fino a farla coincidere con un bordo del tavolo. Adesso fai scorrere la squadra fino a che il lato corto non arriva al bordo. Vedrai che il lato corto sarà perfettamente coincidente con l’altro bordo. Se non è così vuol dire che non i muri che hai preso in considerazione non formano un angolo retto.
Come ti avrà di certo detto la tua prof, un angolo è retto quando misura 90° (si legge novanta gradi). Se ti stai chiedendo perchè un angolo retto misura proprio 90° e non per esempio 100°, potresti leggere questo mio articolo.
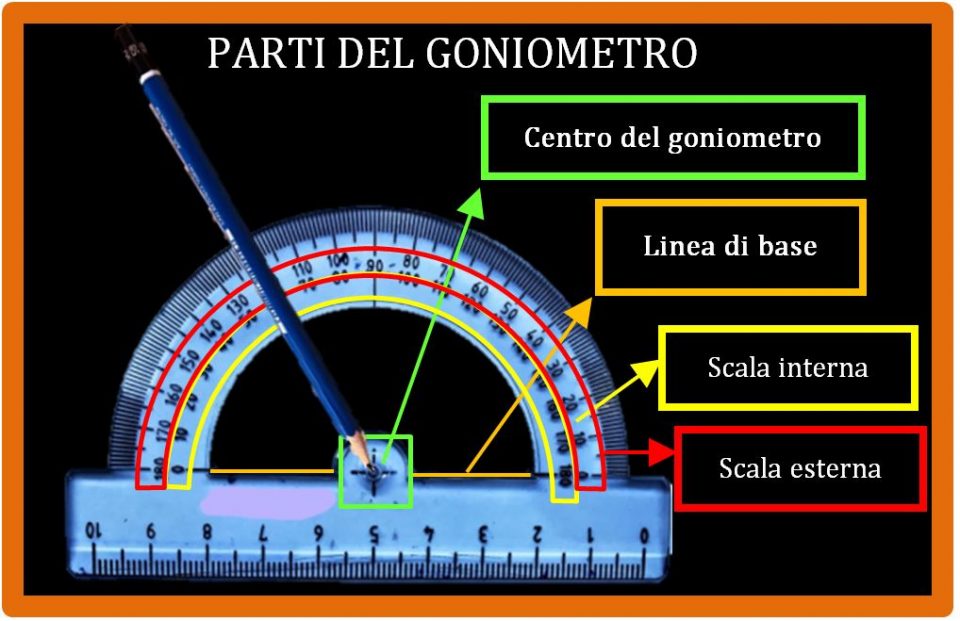
Il goniometro
Per misurare gli angoli si usa uno strumento che si chiama goniometro.

Quello che vedi nell’immagine sopra è il mio goniometro, ma tutti i goniometri si somigliano. Alcuni sono rotondi, ma non cambia nulla, vanno bene lo stesso. Se vuoi ripassare l’uso del gonoimetro, potresti dare un’occhiata al mio articolo come si usa il goniometro.
Disegnare un angolo retto
Cerchiamo di capire come si disegna un angolo retto senza sbagliare. Quando scrivi su un foglio a quadretti è abbastanza semplice disegnare un angolo retto. Naturalmente puoi disegnarlo a mano libera, però in geometria, così come in tecnica è sempre meglio usare gli strumenti appropriati. Quindi per tracciare gli angoli è consigliabile usare il righello o le squadrette.
Di solito prima si disegna una linea, più correttamente dovremo dire una semiretta che ha un inizio, ma non ha una fine.
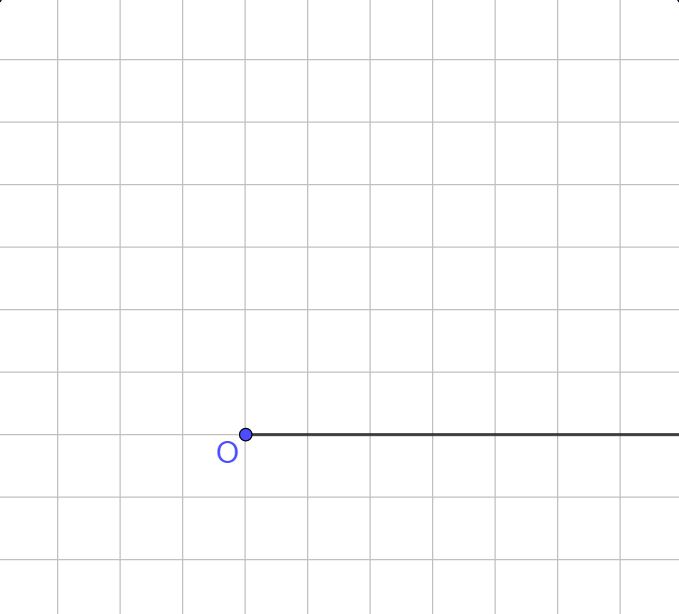
Il punto in cui comincia la semiretta di solito viene chiamato O come origine. Tu sei libero di chiamarlo come vuoi, potresti chiamarlo anche Z o Giulio, ma come ti ho già detto in Italia per indicare i punti in geometria si usano le lettere maiuscole dell’alfabeto e di solito per indicare il punto in cui inizia una semiretta si usa la lettera O.
Se vogliamo disegnare un angolo retto, cioè un angolo che misuri 90° esatti, dobbiamo disegnare un’altra semiretta come quella che vedi sotto. Ci possiamo aiutare seguendo il rigo del foglio e usando anche questa volta il righello.
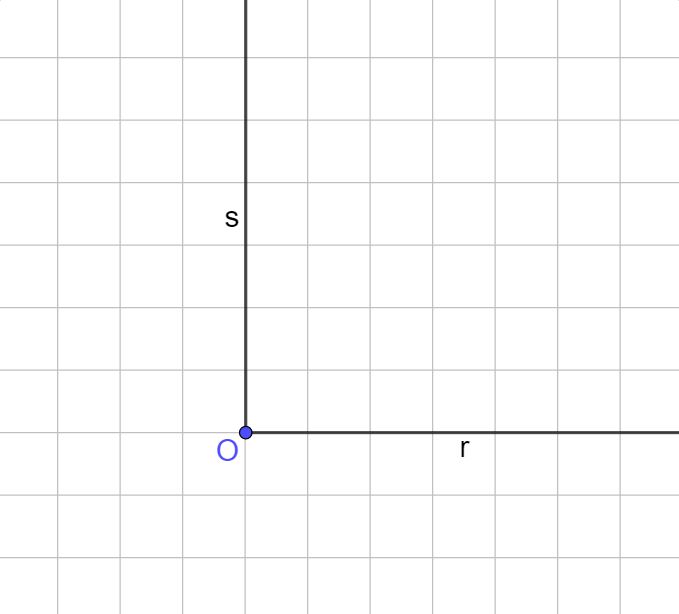
Benissimo abbiamo disegnato un angolo retto. Questo angolo è particolare, infatti a differenza di tutti gli altri angoli che si indicano con un archetto, questo si indica con due piccole linee dritte.
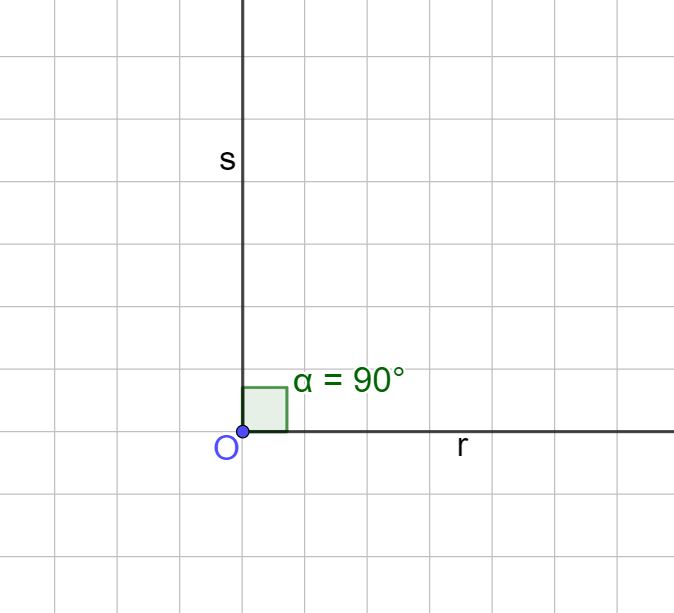
Il programma che uso per disegnare gli angoli al computer si chiama GeoGebra Classico 5. È un programma gratuito che tutti possono scaricare sul pc collegandosi alla pagina ufficiale del programma, raggiungibile a questo link.
Semirette perpendicolari
Le semirette r ed s che formano un angolo retto, sono dette perpendicolari oppure ortogonali oppure normali, sono tre modi diversi di dire la stessa cosa. Detta in un altro modo, la semiretta r è perpendicolare alla semiretta s, vale anche il viceversa, cioè la semiretta s è perpendicolare alla semiretta r.
Usando i simboli tutto quello che abbiamo detto si scrive semplicemente così:
r ⊥ s oppure s ⊥ r
Il simbolo di perpendicolarità è una specie di T maiuscola capovolta. Invece non esiste un simbolo che indica la non perpendicolarità.
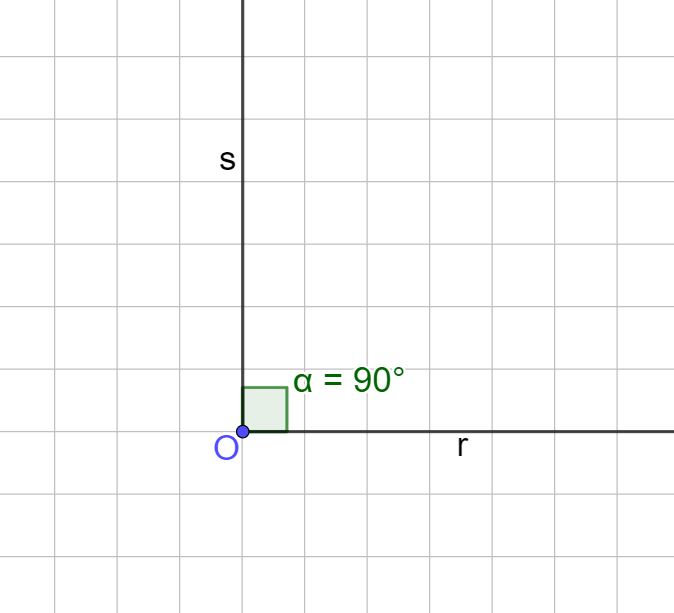
Il ragionamento fatto per le semirette, vale anche per i segmenti e per le rette.
Facciamo alcuni esempi.
Segmenti perpendicolari e non perpendicolari
Continuiamo con alcuni esempi per capire meglio gli angoli retti e le rette perpendicolari. In questo esempio lavoreremo con i segmenti e non con le rette, ma il ragionamento è sempre lo stesso. Disegniamo un segmento che inizia nel punto A e finisce nel punto B (gli estremi del segmento sono i punti A e B).
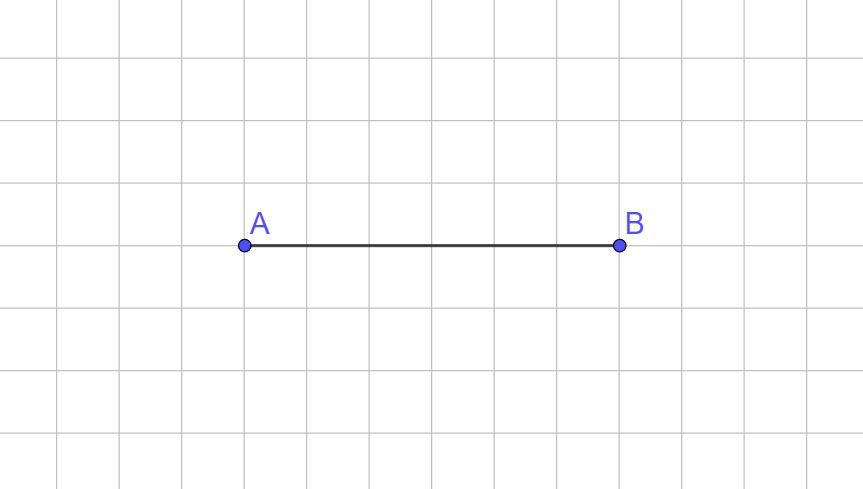
Adesso disegnerò altri tre segmenti, solo uno però sarà perpendicolare al segmento AB. Cerca di capire quale.
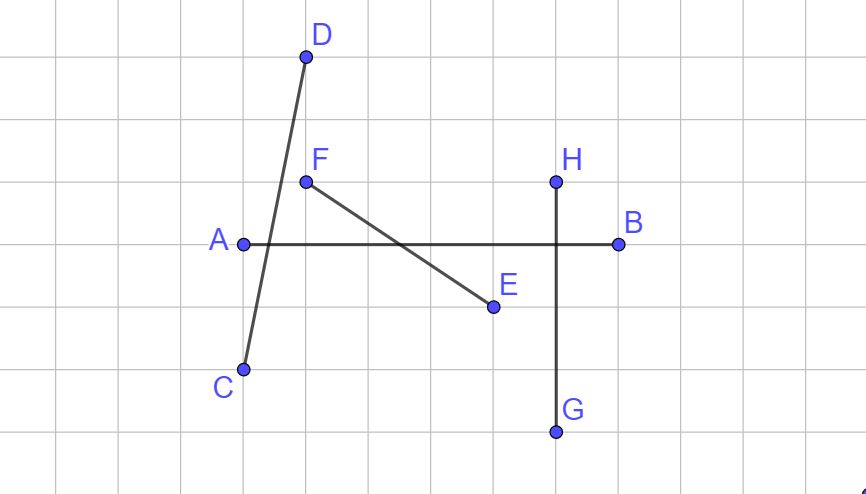
La situazione potrebbe sembrare un po’ confusionaria, ma guardando con attenzione i quadretti e i segmenti potresti già arrivare a capire qual è il segmento perpendicolare al segmento AB.
Se non riesci a individuare il segmento perpendicolare ad AB non ti preoccupare, infatti nella figura non sono indicati gli angoli. Vediamo se indicandoli la situazione va un po’ meglio.
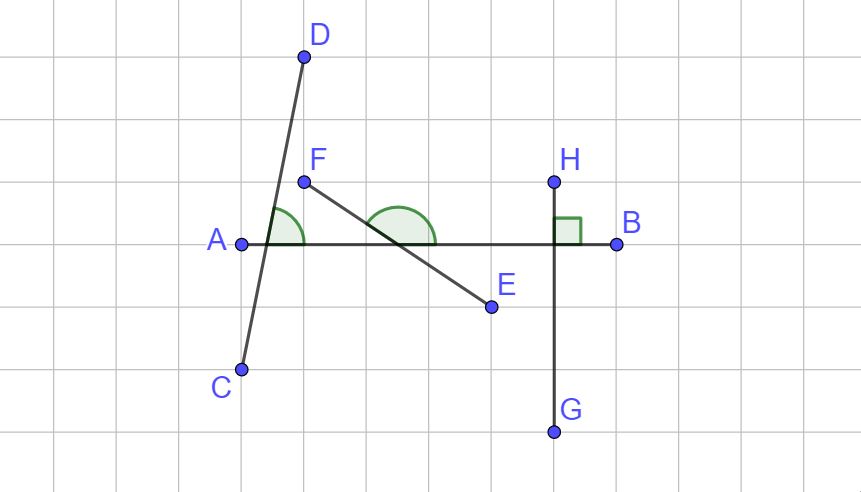
Adesso dovrebbe essere tutto più chiaro. Infatti ti ricordo che due segmenti sono perpendicolari se formano un angolo retto. L’angolo retto è l’unico angolo che non si indica con un archetto, ma si indica con due piccole linee dritte. Possiamo quindi dire che:
il segmento GH è perpendicolare al segmento AB, usando i simboli diventa:
GH ⊥ AB
Benissimo.
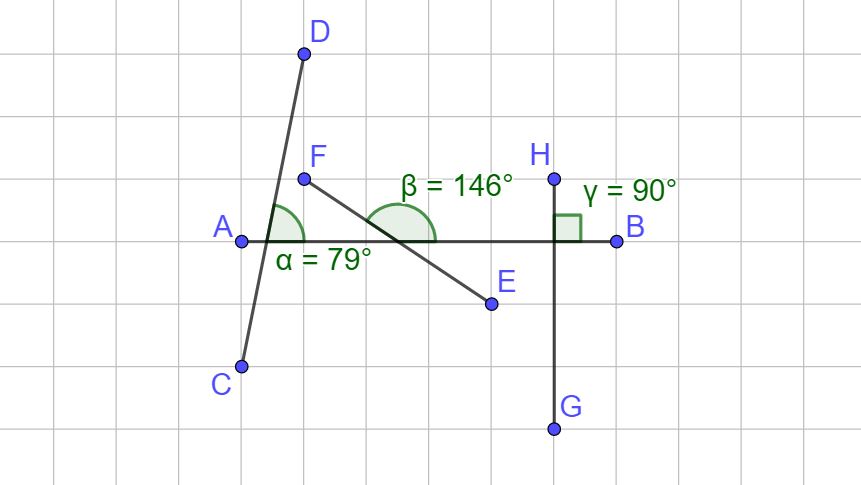
Quella che vedi sopra è la stessa immagine di prima in cui sono stati inseriti anche i valori degli angoli. L’angolo alfa misura 79° (si legge 79 gradi), l’ angolo beta misura 146° e infine l’ angolo gamma misura 90°.
Rette perpendicolari e non perpendicolari
Vediamo un’ altra immagine che ci può aiutare a capire gli angoli retti e le rette perpendicolari e non perpendicolari.
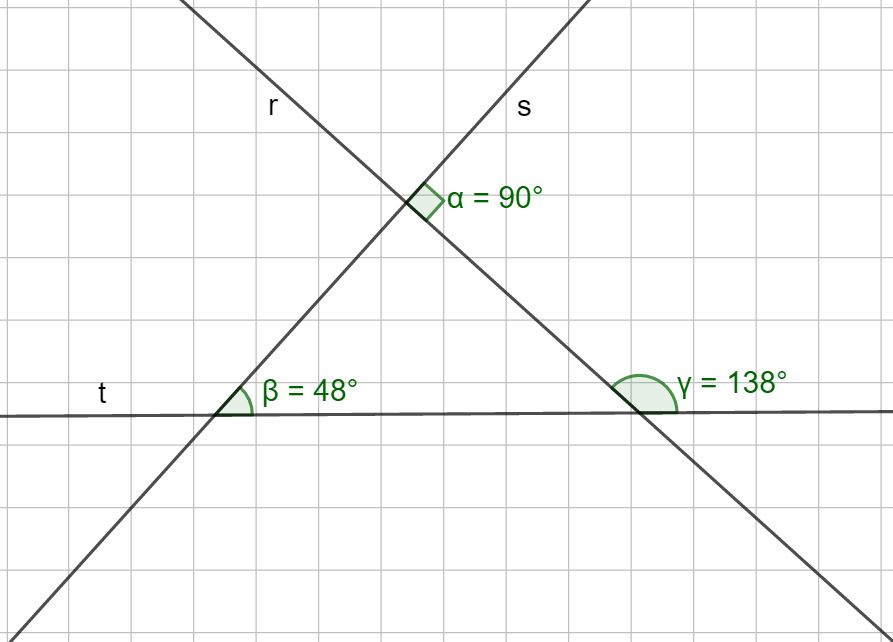
Nell’immagine sopra, abbiamo tre rette, indicate con le lettere dell’alfabeto: r, s,e t. Oseerviamo con attenzione la figura e cerchiamo di capire quali rette sono perpendicolari tra loro.
- La retta t e la retta s si incrociano (si intersecano) e formano un angolo di 48°, quindi non sono perpendicolari.
- La retta t e la retta r si incrociano e formano un angolo di 138°, quindi non sono perpendicolari.
- La retta r e la retta s si incrociano e formano un angolo di 90°, quindi sono perpendicolari.
Esercizi
Adesso se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Prima di rispondere alle domande osserva bene l’immagine, lavora con calma e non ti preoccupare se sbagli. Sbagliando si impara.
![]() Angoli retti e segmenti perpendicolari – Esercizi.pdf
Angoli retti e segmenti perpendicolari – Esercizi.pdf
![]() Angoli retti e segmenti perpendicolari – Risposte.pdf
Angoli retti e segmenti perpendicolari – Risposte.pdf
Buon lavoro.
Link utili
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe. Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola periodica interattiva degli elementi, sempre fornita dalla Zanichelli. Se vuoi ripassare l’alfabeto greco puoi visitare questa pagina.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it , saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
Nella pagina sono presenti link di affiliazione su cui si ottiene una piccola quota dei ricavi, senza variazioni dei prezzi.