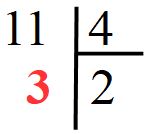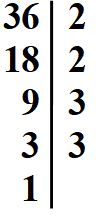In questo articolo vedremo come si esegue il calcolo del minimo comune multiplo tra tre numeri. Se sai già calcolare l’m.c.m. tra due numeri, allora passiamo subito a vedere gli esempi. Se invece preferisci rivedere cosa si intende per minimo comune mutiplo potresti dare un’occhiata agli articoli che vedi sotto. Non c’è niente di cui vergognarsi se non ti ricordi come si calcola l’m.c.m.. È normale scordarsi qualche concetto. Ripassare serve proprio a questo. Anche i prof rivedono la lezione prima di entrare in classe, per cui ripassiamo senza vergognarci.
Lo so che hai fretta e che vorresti imparare tutto e subito, ma la matematica non è un videogame. Ci sono alcune cose che bisogna sapere, altrimenti non si può andare avanti. Non puoi calcolare il minimo comune multiplo se non sai come si scompongono i numeri in fattori primi. E per scomporre i numeri in fattori primi, devi sapere cosa sono i numeri primi. Quindi io ti consiglio di non avere premura e impiegare 10 minuti di tempo per andare a rivedere questi importanti concetti.
Indice
Esempio 1
Cominciamo con il primo esempio. Il procedimento di calcolo del minimo comune multiplo tra tre numeri è lo stesso di quello che si usa per due numeri. L’unica cosa che cambia è che i numeri da scomporre sono tre. Facciamo un esempio numerico. Calcoliamo l’m.c.m. tra 192, 256 e 240, si scrive così:

La prima cosa che dobbiamo fare è scomporre in fattori primi i tre numeri che abbiamo nell’esercizio. I metodi per scomporre in fattori primi sono tanti, i più usati sono quello in colonna e quello ad albero. Sono entrambi corretti. In questo esempio io userò il metodo in colonna, nell’esempio successivo il metodo ad albero.
Scomposizione in fattori primi
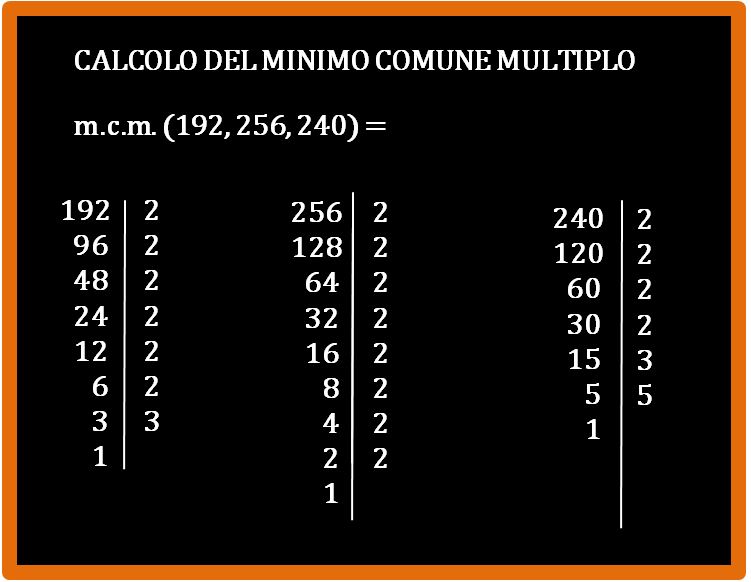
Dopo avere eseguito la scomposizione, scriviamo i nostri tre numeri (192, 256 e 240) come il risultato di una moltiplicazione dei fattori che li compongono. Usiamo i numeri per scrivere quello che abbiamo detto a parole:
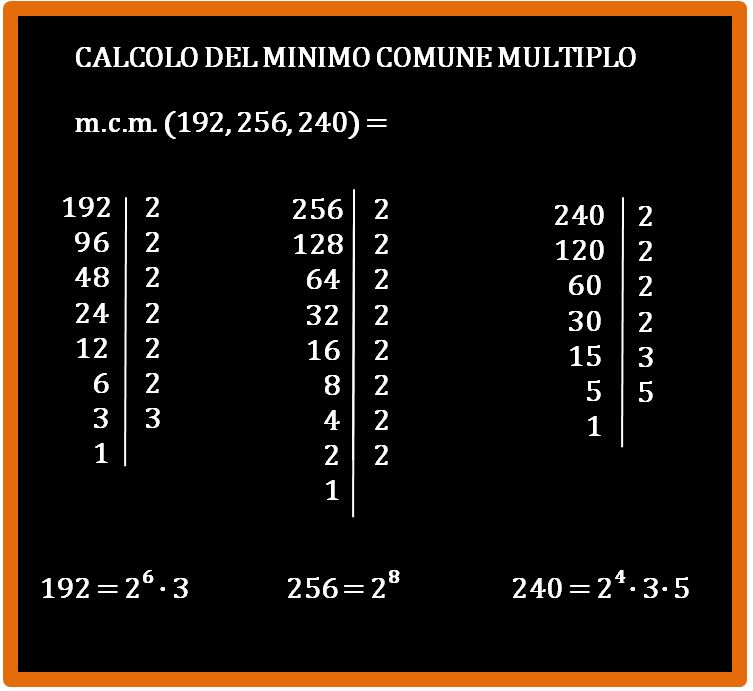
Scelta dei fattori
Fantastico. Liberiamo la lavagna dalle colonne della scomposizione e passiamo a scegliere i fattori che ci interessano per il calcolo del minimo comune multiplo.

Ora è arrivato il momento di applicare la regola:
Per calcolcare il minimo comune multiplo, vanno presi in considerazione sia i fattori comuni (che compaiono in tutte e tre le scomposizioni) sia i fattori non comuni (cioè quelli che compaiono in una sola oppure in due scomposizioni) presi una sola volta, con l’esponente maggiore.
Vediamo cosa vuol dire nei fatti.
Partiamo dal fattore 2. Compare in tutte e tre le scomposizioni:
- nella scomposizione del 192 con esponente 6 (26),
- nella scomposizione del 256 con esponente 8 (28) e
- nella scomposizione del 240 con esponente 4 (24).
Quale scegliamo? Ne dobbiamo scegliere solo uno (presi una sola volta, dice la regola). Dobbiamo scegliere solo quello che ha l’esponente maggiore. Quindi due all’ottava (28), gli altri non vanno considerati. Le prime volte può essere utile tracciare una piccola croce sui fattori che non consideriamo.

Bene. Adesso passiamo al fattore 3 che compare:
- nella scomposizione del 192, con esponente 1 e
- nella scomposizione del 240 ancora con esponente 1.
Quale scegliamo? Uno dei due, uno vale l’altro. L’importante è che ne consideriamo solo uno e non tutti e due. Quindi uno lo cerchiammo e uno lo barriamo.

Fantastico. Stiamo procedendo molto bene.
Ci rimane da considerare il fattore 5, infatti anche se compare solo nella scomposizione del 240, va comunque considerato. Quindi tracciamo un cerchio attorno al 5.

Abbiamo scelto nel modo corretto i nostri fattori. Adesso li moltiplichiamo tra loro e abbiamo trovato il minimo comune multiplo.

Il risultato che stavamo cercando è 3840. Come dici? Ti sembra un numero troppo grande? Non ti preoccupare con il minimo comune multiplo capita di avere di numeri grandi.
Esempio 2
Calcoliamo il minimo comune multiplo tra 10, 6 e 14. Procediamo alla scomposizione in fattori primi. Utilizzerò lo schema ad albero, ma anche quello in colonna va bene. Se si esegue la scomposizione in modo corretto, si arriva allo stesso risultato.
scomposizione in fattori primi
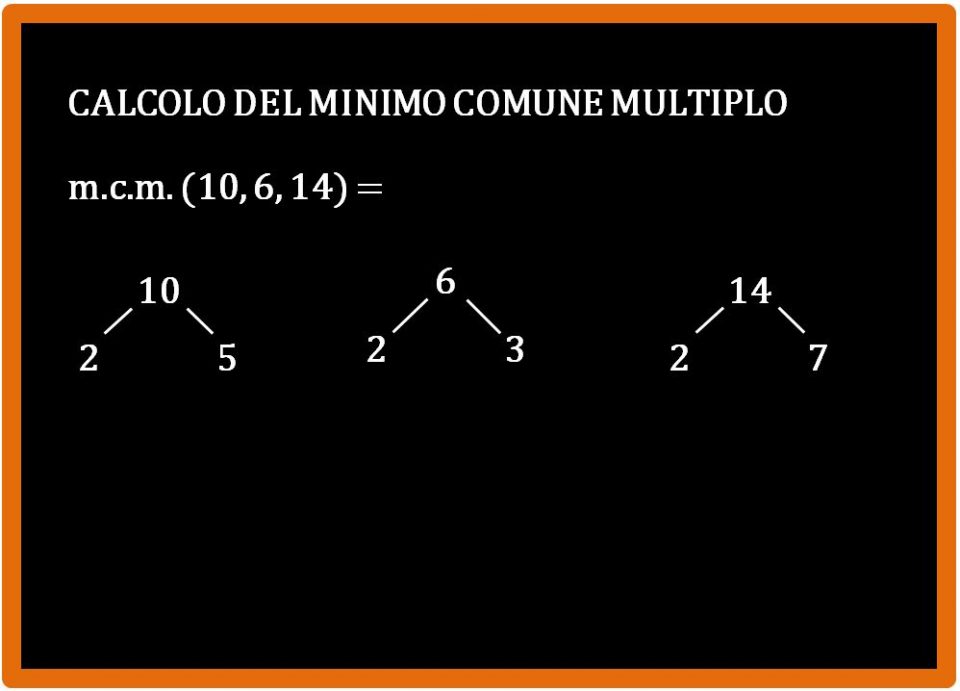
Scelta dei fattori
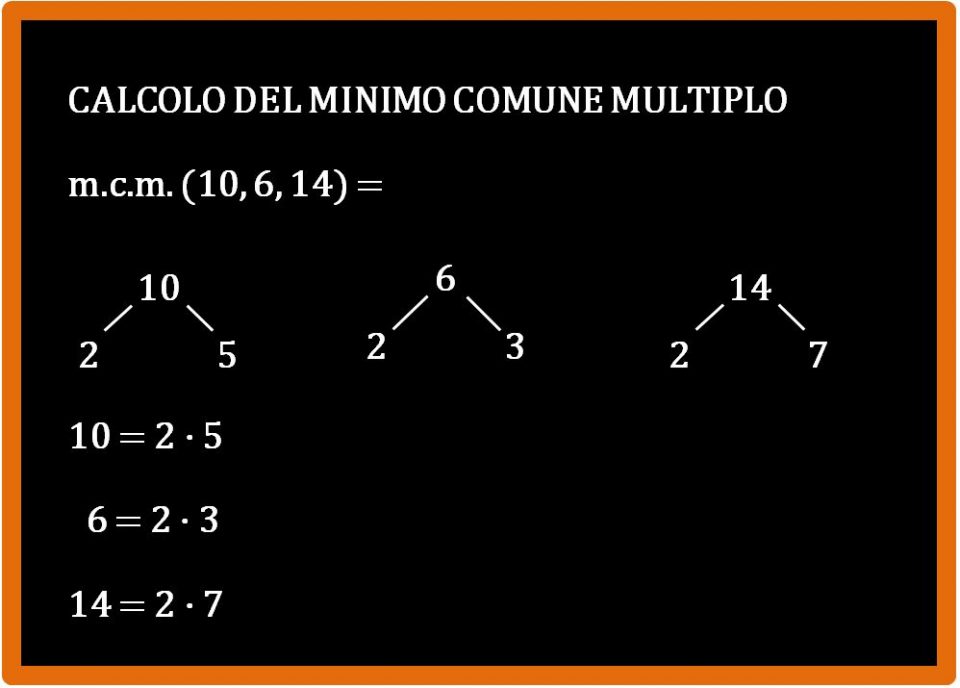
Seguendo le stesse regole dell’esempio 1, scegliamo i fattori corretti per il calcolo dell’m.c.m. Cerchiamo quelli da considerare e barriamo quelli che invece non vanno considerati.

Fantastico. Moltiplichiamo tra loro i fattori scelti e avremo trovato il minimo comune multiplo.

Il risultato che stavamo cercando è 210. Adesso possiedi tutti gli strumenti necessari per calcolare il minimo comune multiplo tra tre numeri qualsiasi.
Esercizi in pdf
Adesso, se vuoi puoi metterti alla prova, con gli esercizi che trovi nel file pdf sotto. Lavora con calma e non avere fretta di finire. E se sbagli non ti preoccupare. Nessuno verrà a rimproverarti. I risultati ti servono per capire se hai lavorato bene oppure no.
![]() Minimo comune multiplo tra 3 numeri – Esercizi.pdf
Minimo comune multiplo tra 3 numeri – Esercizi.pdf
![]() Minimo comune multiplo tra 3 numeri – Risultati.pdf
Minimo comune multiplo tra 3 numeri – Risultati.pdf
Buon lavoro.
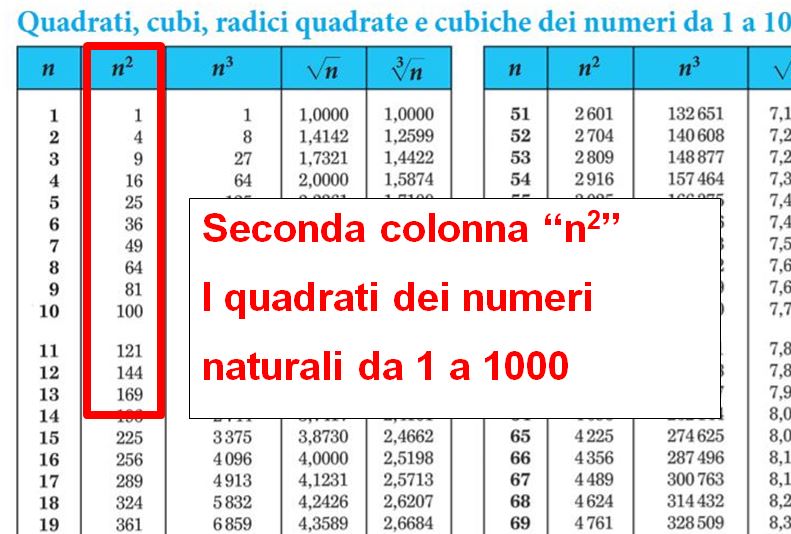
Cliccando qui si aprirà una pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori.