In questo articolo cecheremo di capire come si disegna l’asse di un segmento. Vedrai che con 5 minuti di impegno ti sarà tutto chiaro. Però, dato che si parla di disegno geometrico, la cosa migliore da fare sarebbe provare a disegnare l’asse e non solo leggere come si fa. Il mio consiglio quindi è quello di procurarti un foglio a quadretti (va bene sia da 4 mm, sia da 5mm), una matita, una gomma e due squadre.
indice
cose da sapere
Prima di cominciare a disegnare è necessario ripassare un paio di concetti: il punto medio e segmenti perpendicolari. Niente di difficile.
- Il punto medio di un segmnto è quel punto che divide il segmento in due parti uguali. Detto in altre parole, è quel punto che divide il segmento a metà. Se un segmneto è lungo 10 cm, il punto medio si trovera a 5 cm.
- Due segmenti sono perpendicolari se formano un angolo retto, cioè un angolo di 90°.
Tutto qui. possiamo cominciare a fare sul serio.
esempio 1
Tracciamo il punto medio del segmento AB. Io utilizzerò il software GeoGebra Classico 6 che è gratuito e scaricabile da chiunque collegandosi alla pagina ufficiale del software. Per iniziare tracciamo il segmento AB che ha come estremi i punti A e B:
A( 1; 1 )
(si leggee: punto A di coordinate 1 1 oppure punto A di ascissa 1 e ordinata 1)
B( 9; 1 )
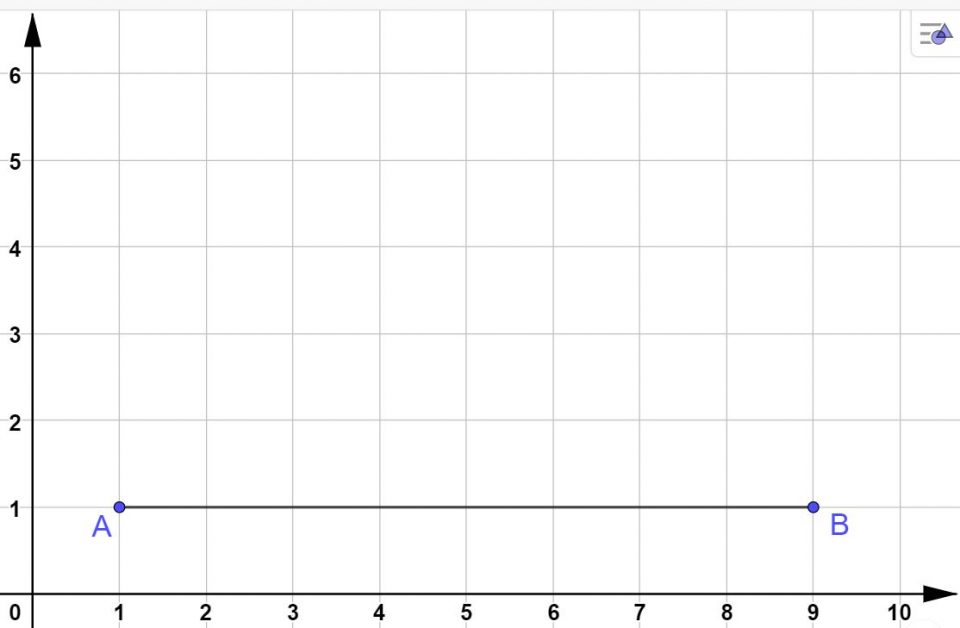
Molto bene. La prima cosa da fare è andare a individuare il punto medio di AB, cioè quel punto che lo divide a metà. Possiamo contare i quadretti, oppure usare una squadra o un righello. Dato che il segmento AB è lungo 8 quadretti, la metà si trova contando 4 quadretti partendo da A.
Per indicare il punto medio, di solito si usa la lettera “M”, che è la lettera iniziale della parola medio.
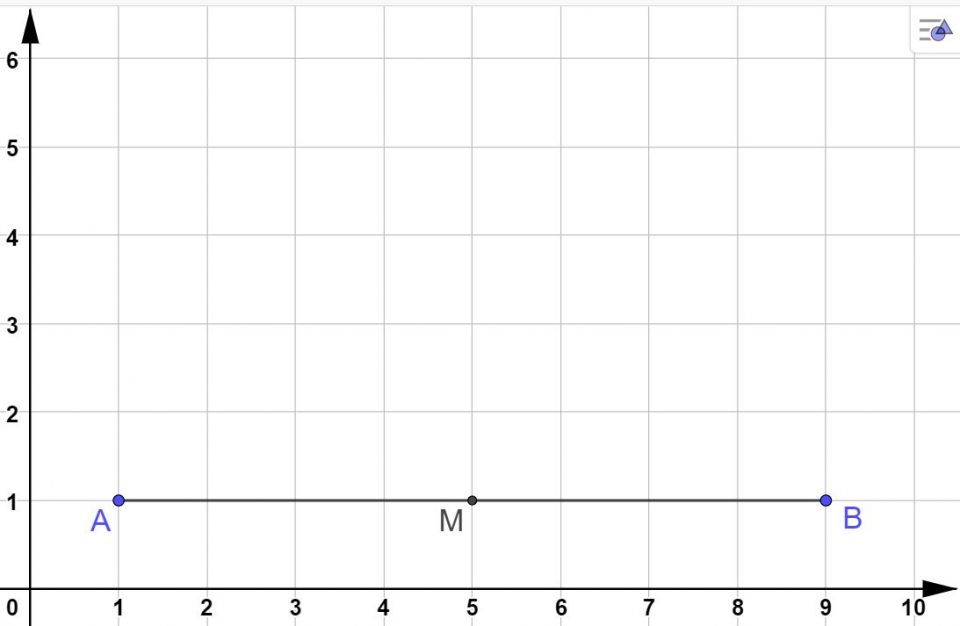
Il punto M, che è il punto medio del segmento AB, ha coordinate:
M( 5; 1) (si legge: M di ascissa 5 e ordinata 1)
Benissimo. Siamo a metà strada. Adesso dobbiamo tracciare una retta che deve passare per M e che deve essere perpendicolare al segmento AB. Nell’immagine sotto è illustrato quello che hai appena letto. Poi vedremo come si usano le squadre per tracciare la retta.
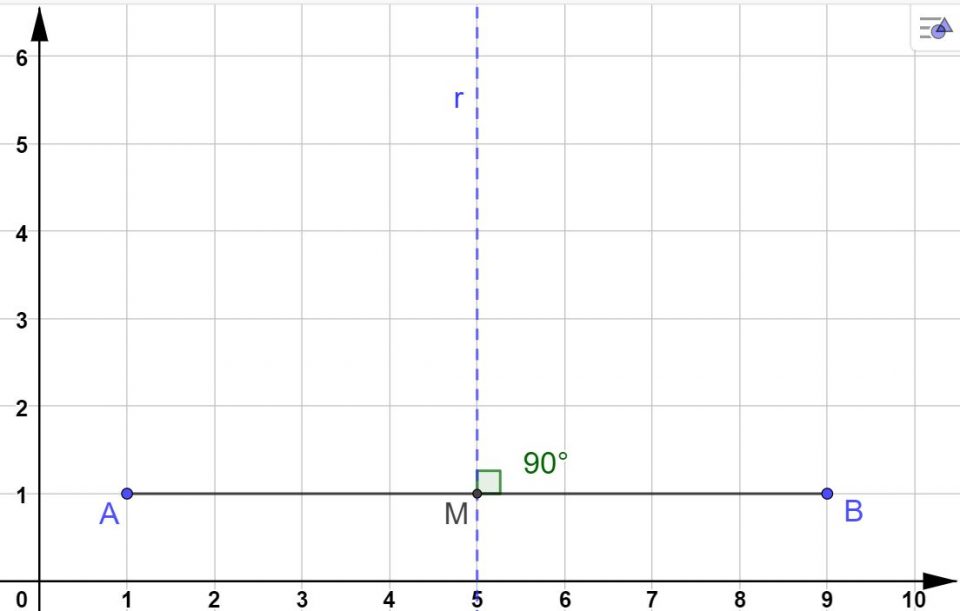
Nel caso di un segmento orizzontale, per tracciare l’asse ci si può aiutare con i quadretti.
Ma vediamo come si procede usando le squadre “a carrello”.
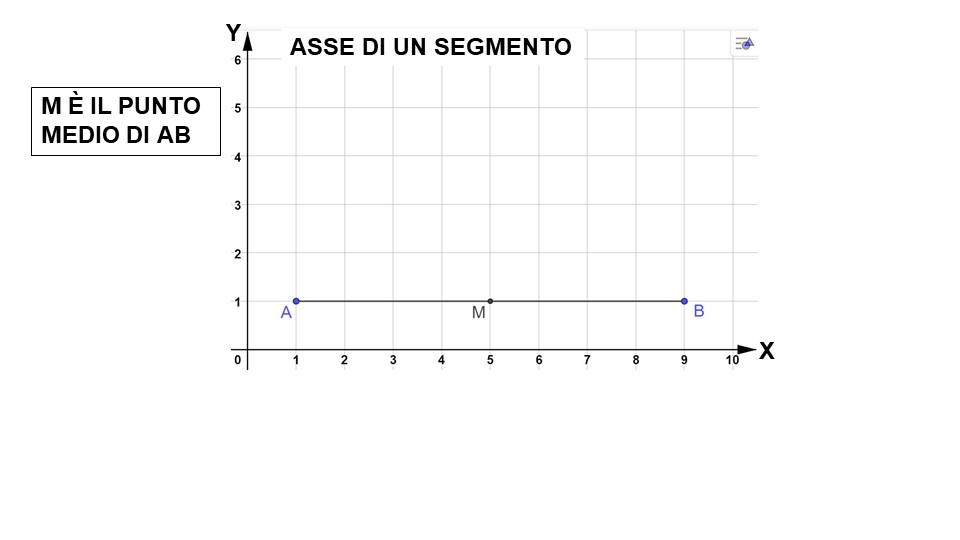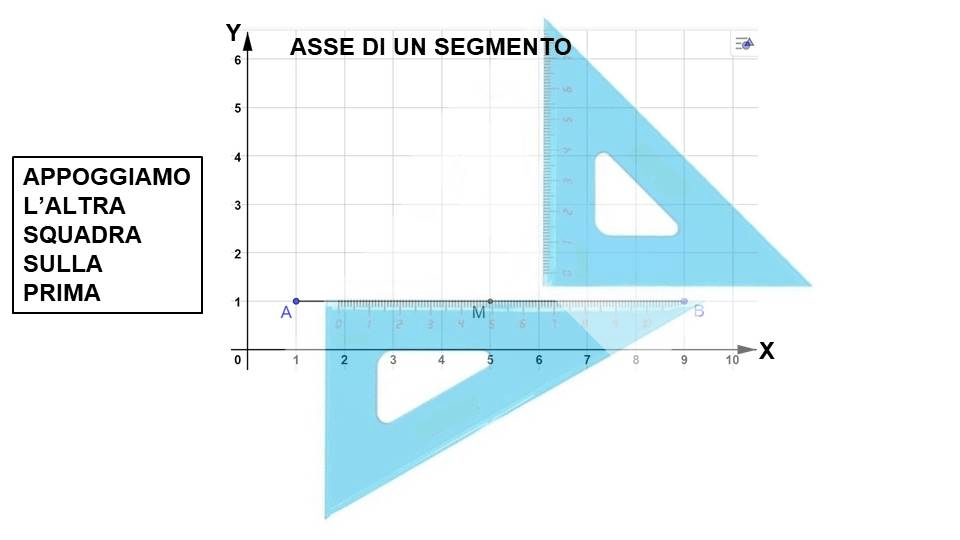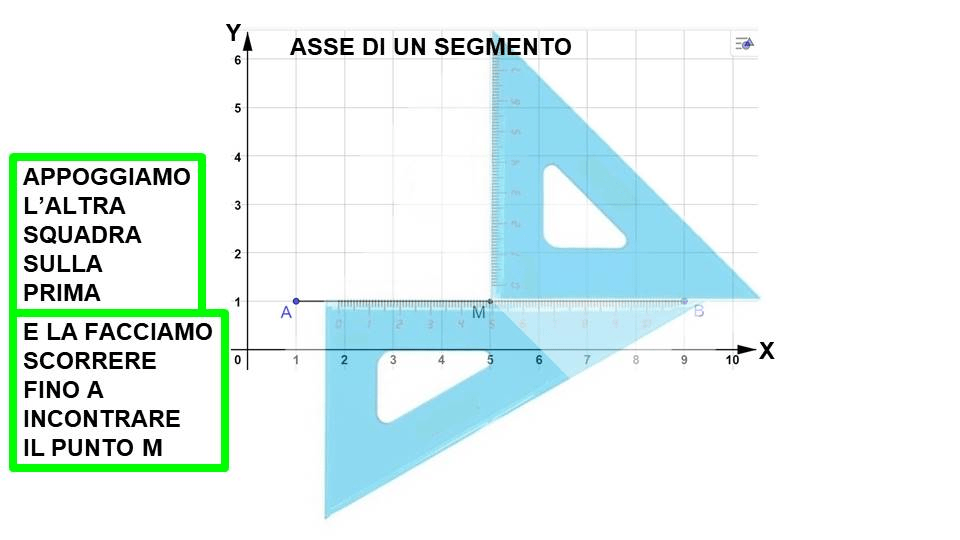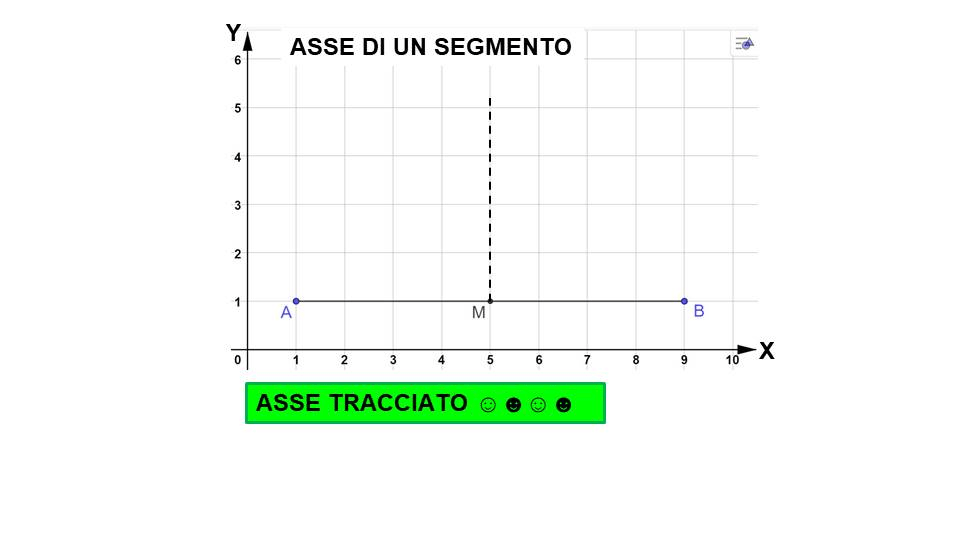
Durante i primi esercizi molto probabilmente posizionerai le squadre in modo sbagliato. Non ti preoccupare, è normale. Abbiamo cominciato tutti così.
secondo asse
Complichiamo un po’ le cose. Tracciamo sullo stesso piano cartesiano il punto
C ( 3; 3) (si legge: punto c di coordinate tre tre)
e uniamo il punto B con il punto C, in modo da ottenere il segmento BC.
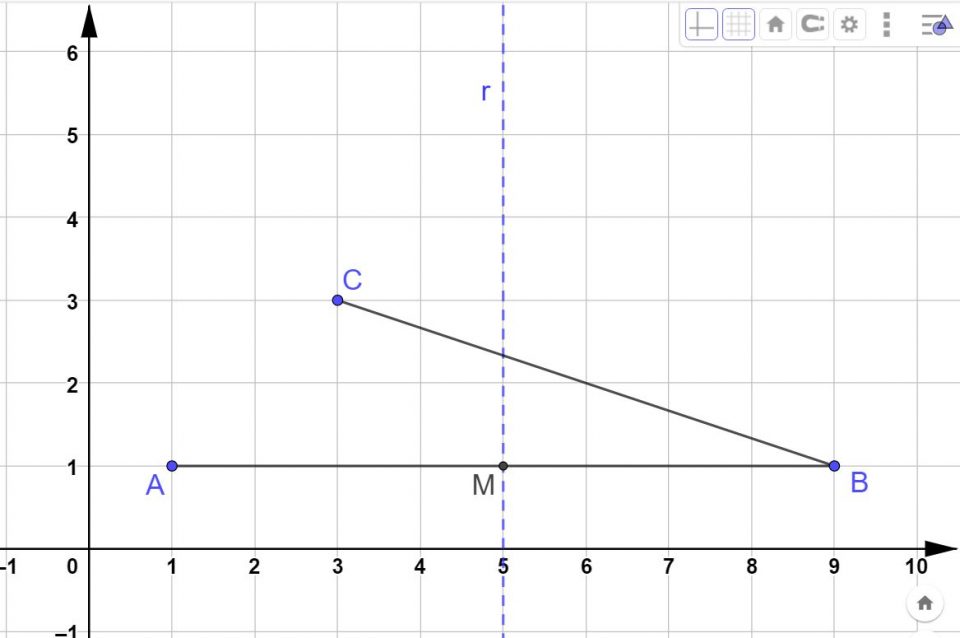
Molto bene. Adesso la prima cosa da fare è trovare il punto medio di BC. Anche in questo caso ci possiamo aiutare con i quadretti oppure possiamo misuare con il righello il segmento.
Chiamiamo N il punto medio di BC. Il punto N ha coordinate:
N ( 6 ; 2)
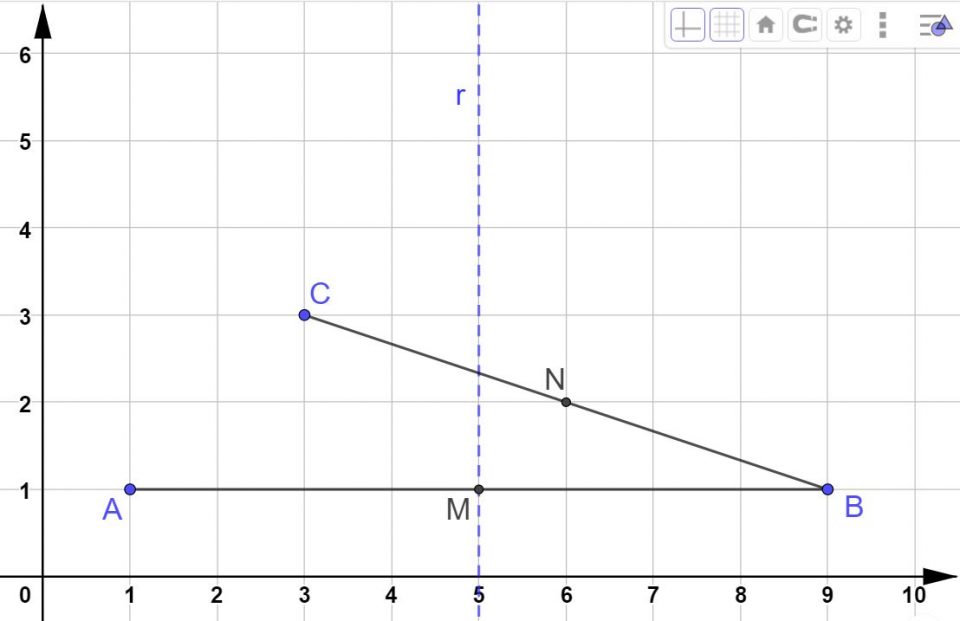
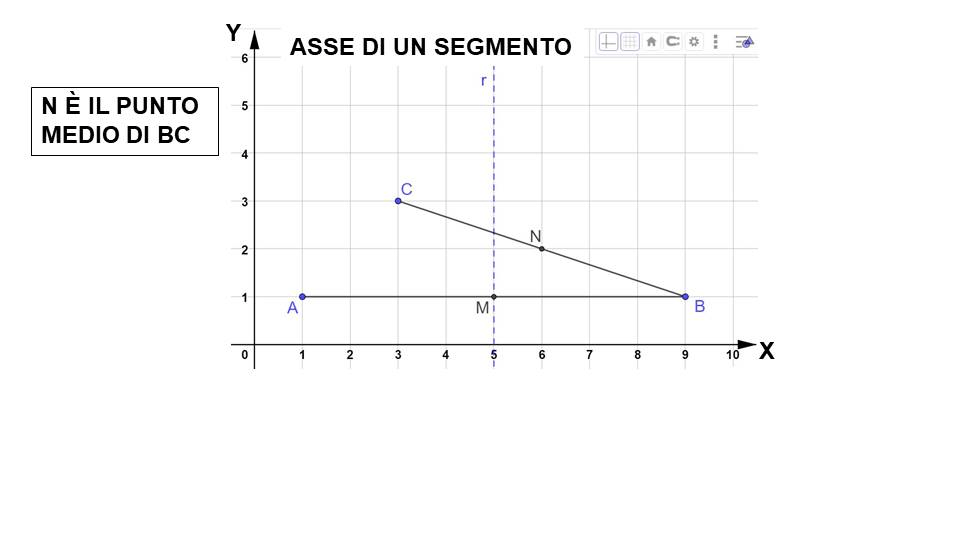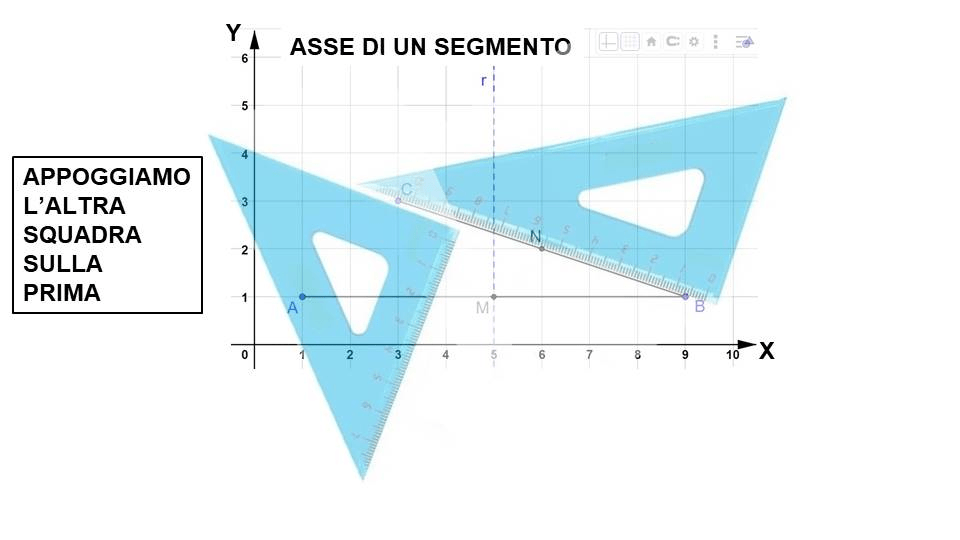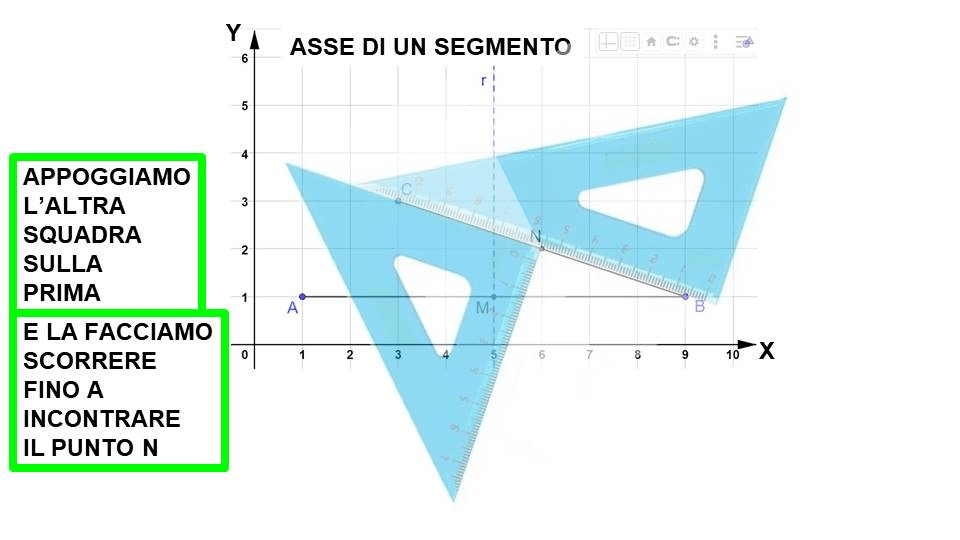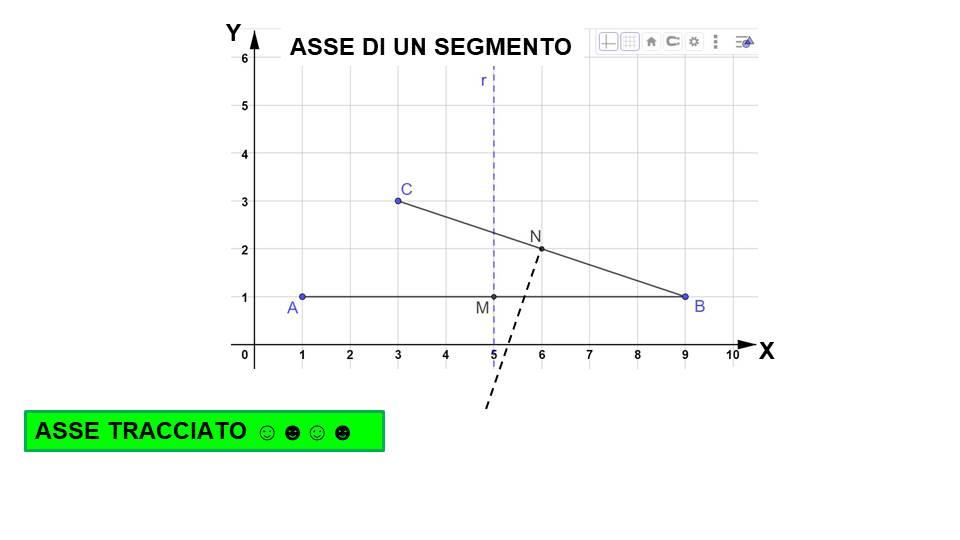
Per tracciare l’asse non ci possiamo aiutare con i quadretti. Dobbiamo necessariamente utilizzare le squadre. Nell’animazione sotto puoi vedere come si disegna l’asse di un segmento.
TERZO ASSE
Adesso, concludiamo tracciando il terzo lato AC. Troviamo il punto medio di AC, che chiameremo O e tracciamo l’asse di AC. Per maggiore chiarezza ho scelto di colorare ogni lato e il suo asse dello stesso colore.
Anche in questo caso ci aiutiamo con una animazione per capire meglio come si disegna l’asse di un segmento.
Abbiamo concluso.
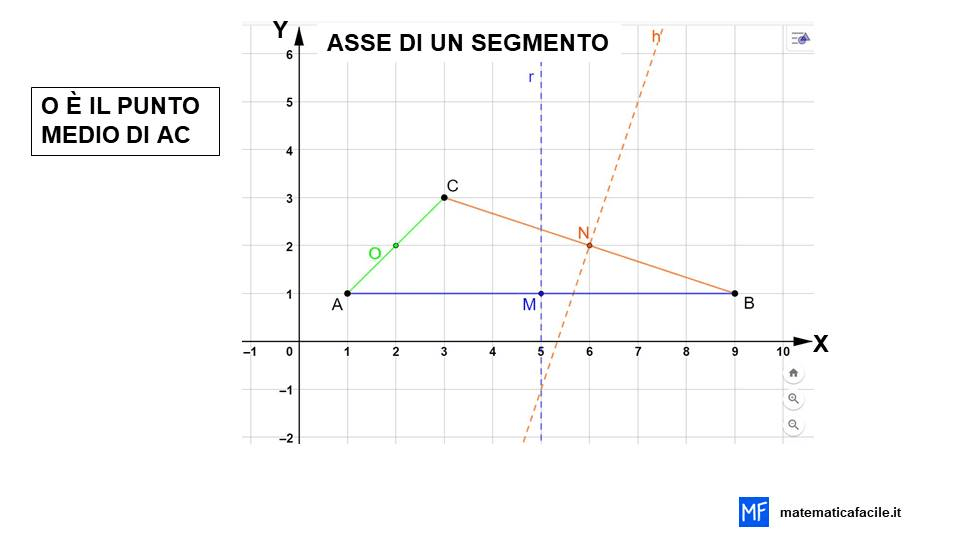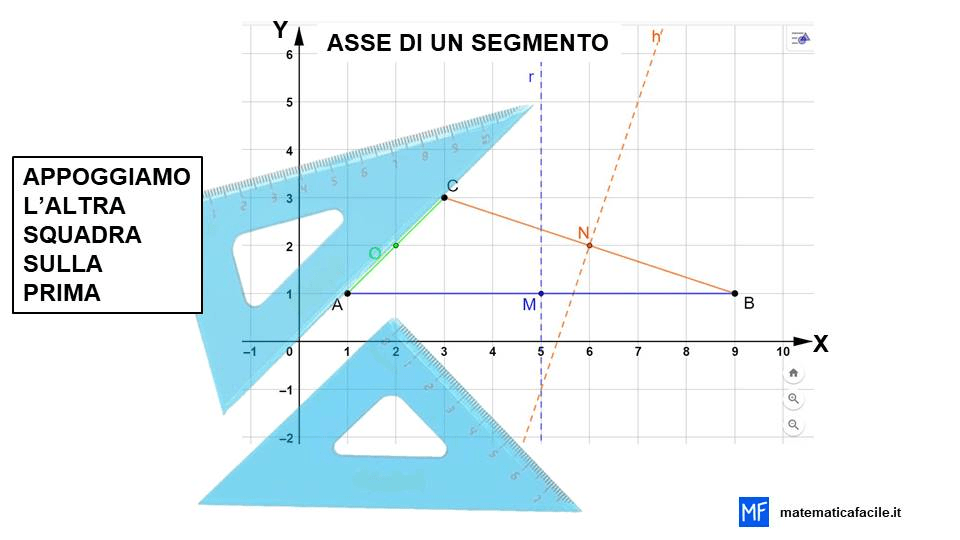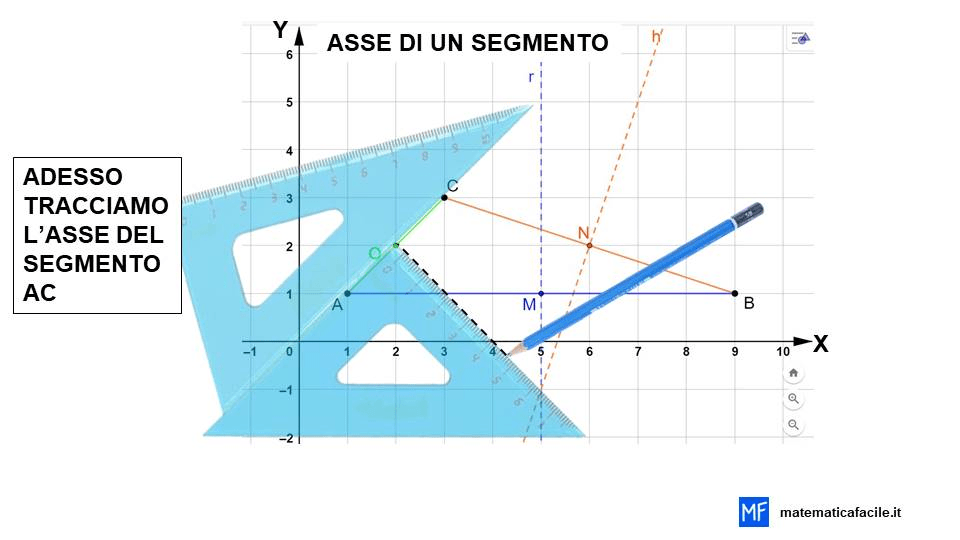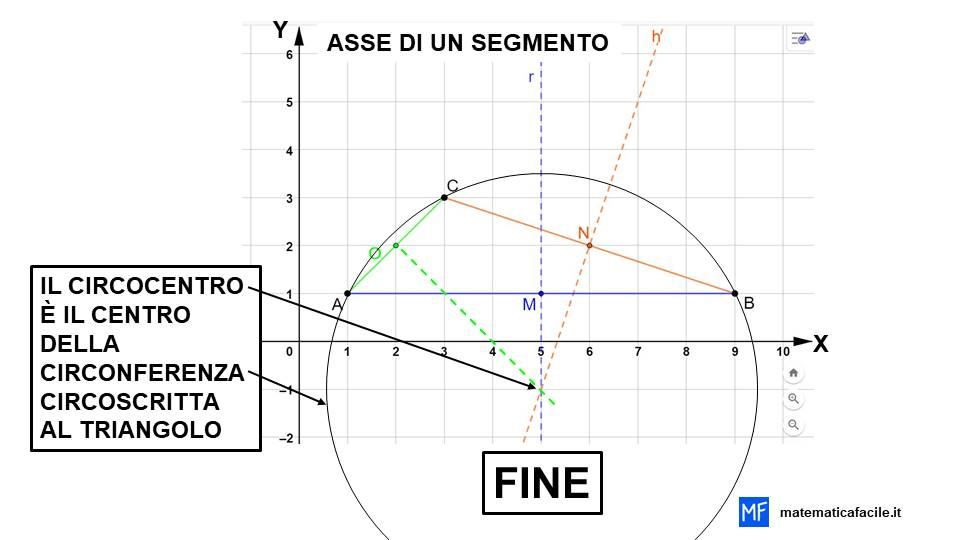
il circocentro
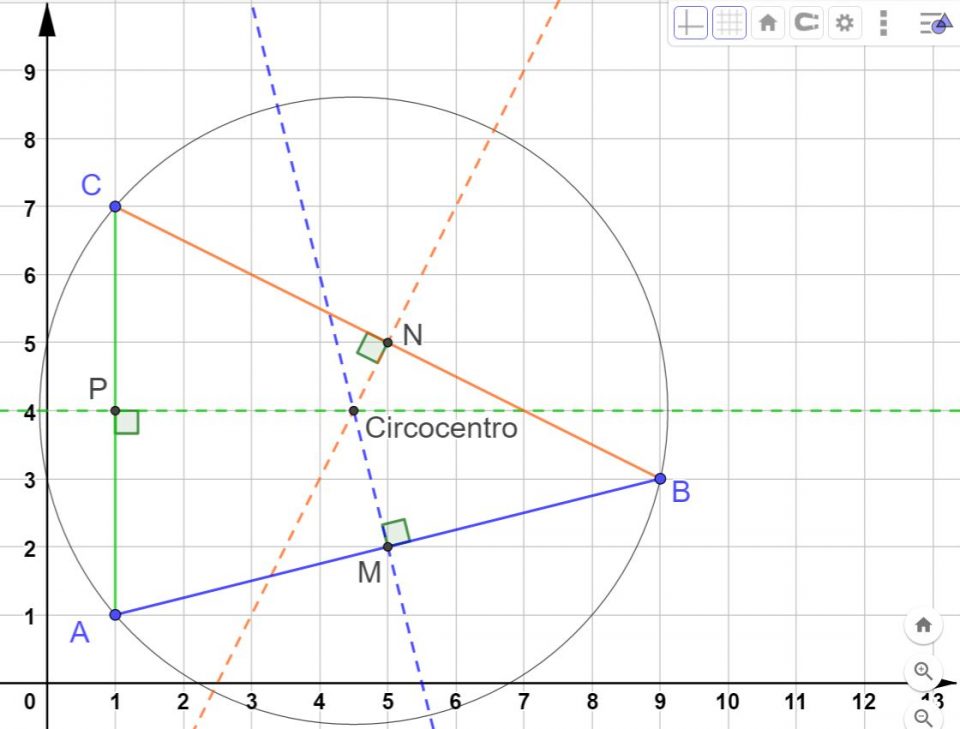
Se hai lavorato bene, i tre assi del triangolo (e questo è vero per qualsiasi triangolo disegnerai) si incontrano tutti in un unico punto che viene chiamato circocentro.
Il circocentro è il centro della circoferenza circoscritta al triangolo. Prova a prendere un compasso, puntalo nel circocentro con apertura uguale alla distanza tra il circocentro e il vertice A. Come vedi nell’immagine sotto.
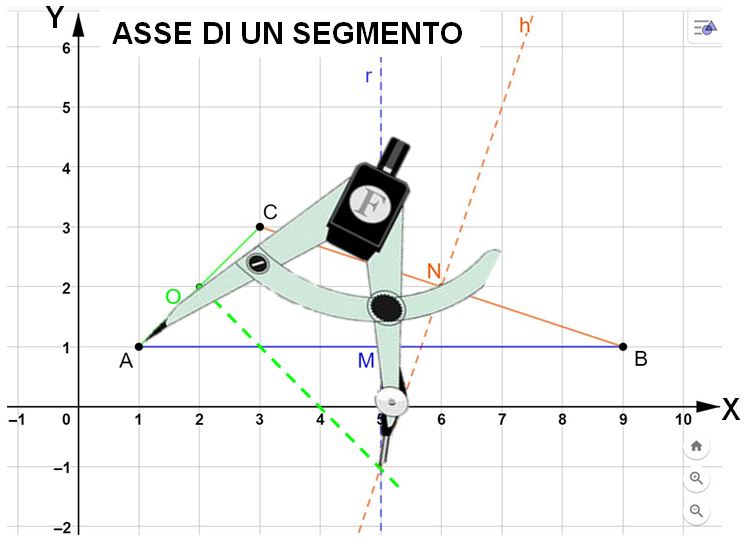
Se adesso tracci la circonferenza, vedrai che la circonferenza tocca tutti i vertici del triangolo. Hai appena disegnato la circonferenza circoscritta al triangolo, cioè che circonda il triangolo.
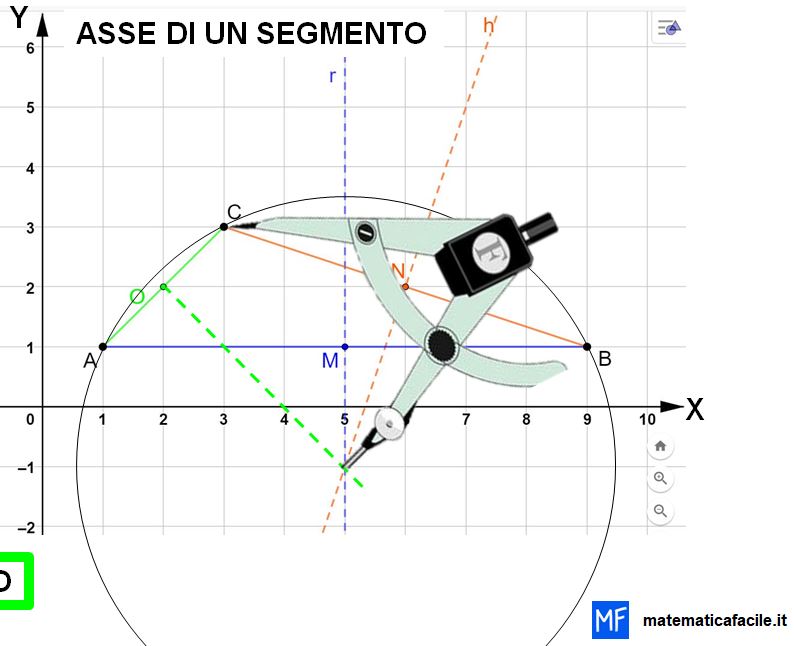
Esercizio concluso.
Esercizio
Adesso se vuoi, puoi metterti alla prova con l’esercizio che puoi leggere sotto. Ti potrà servire per vedere se hai capito come si disegna l’asse di un segmento.
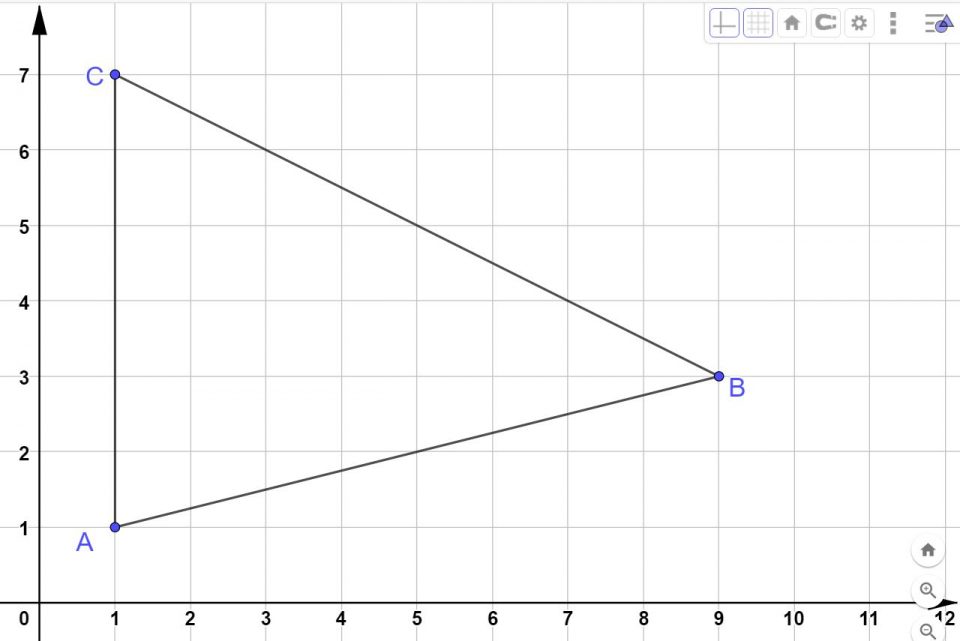
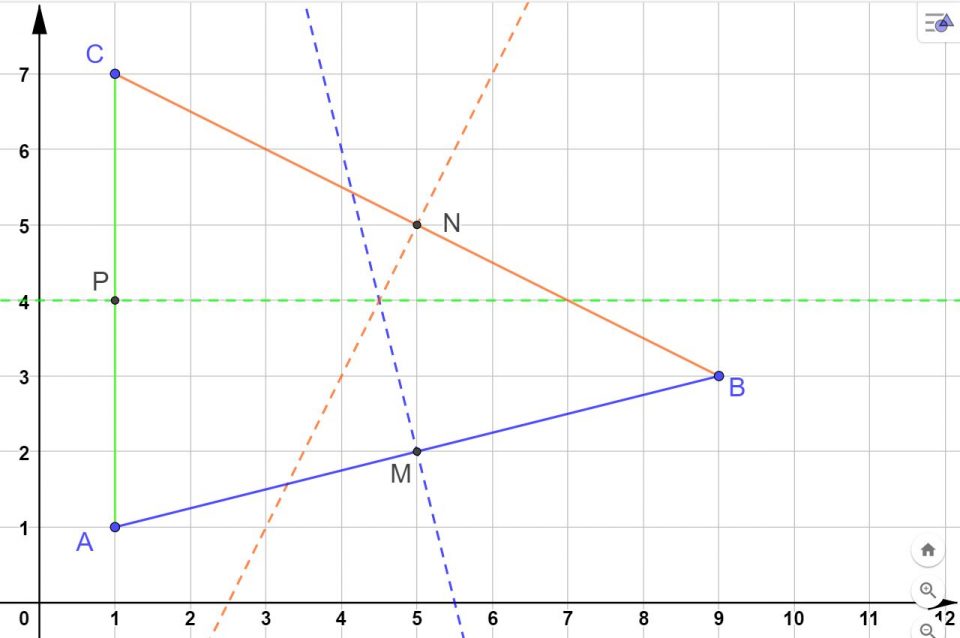
- Traccia su un piano cartesiano i punti: A(1;1) , B (9;3) e C (1;7).
- Unisci il punto A con il punto B, ottieni in questo modo il segmento AA.
- Unisci il punto B con il punto C, ottenendo il segmento BC.
- Unisci il punto C con il punto A, ottenendo così il segmento CA.
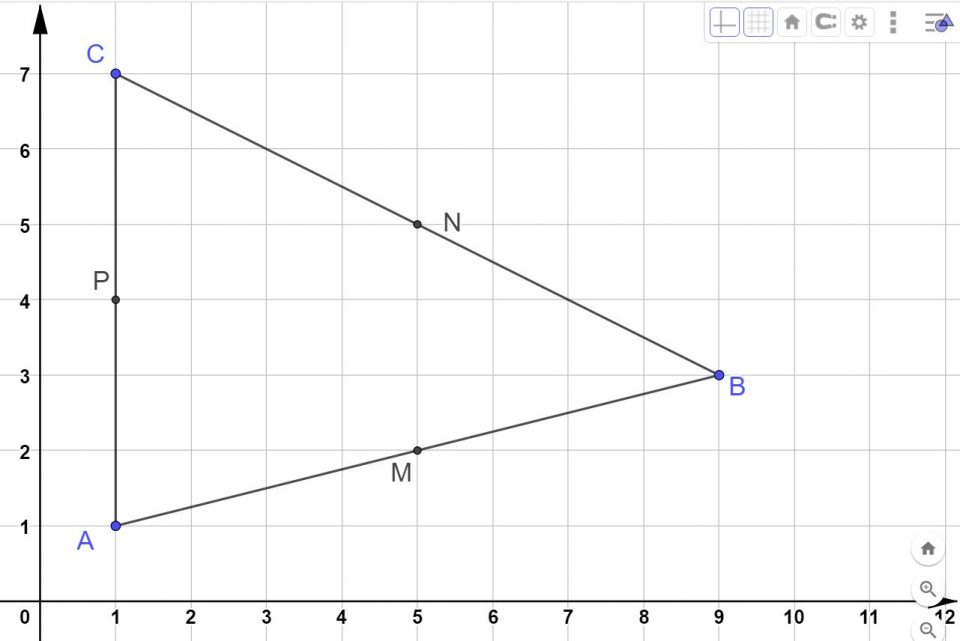
- Hai tracciato un triangolo. Per ogni lato individua il punto medio.
- Dopo avere individuato il punto medio traccia i tre assi.
- Alla fine traccia la circonferenza circoscritta al triangolo.
Se hai lavorato bene, il risultato finale dovrebbe essere simile a quello che puoi vedere nella galleria di immagini sotto. Ricorda che lavorando con matita e squadra, un errore di uno o due millimetri è tollerabile.
Saper lavorare con le squadre a carrello richiede pratica ed esercizio. Non ti arrendere se nei primi esercizi hai qualche difficoltà, è normale, abbiamo cominciato tutti così.
link utili
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe.
Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli.
Se vuoi porre domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.