Oggi la prof ha spiegato come si calcolano le coordinate del punto medio di un segmento. Hai sentito parole strane come semisomma e altre cose del genere e non ci hai capito tanto e sei finito qui. Non ti preoccupare, con 5 minuti di impegno saprai calcolare le coordinate del punto medio di qualsiasi segmento.
Indice
- Primo esempio
- Ripasso
- Calcolo delle coordinate
- Ascissa del punto medio
- Ordinata del punto medio
- Riepilogo
- Primo esercizio
- Secondo esercizio
Esempio 1
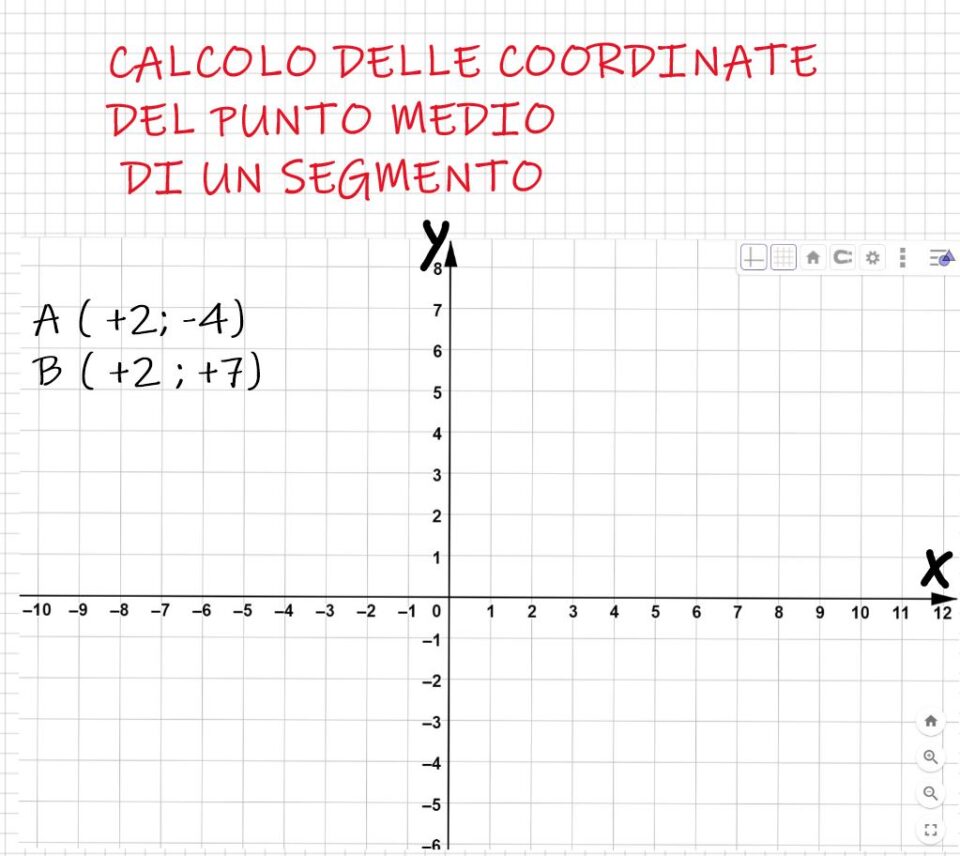
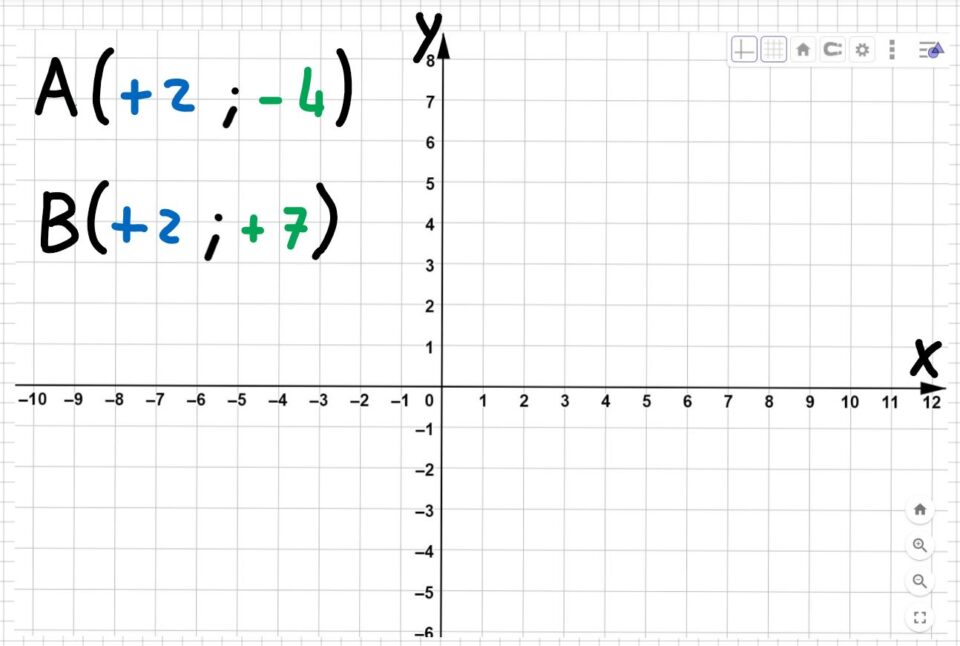
Supponiamo di voler trovare il punto medio del segmento AB che ha i suoi estremi nel
punto A ( +2; -4) e nel
punto B ( +2; +7) .
Ripasso
Facciamo un ripasso veloce. Ogni punto sul piano cartesiamo è individuato da una coppia di numeri, chiamati coordinate.
- Il primo numero è chiamato ascissa e indica quanto ci si deve spostare sull’asse X, invece
- il secondo numero è chiamato ordinata e indica quanto ci si deve spostare sull’asse Y.
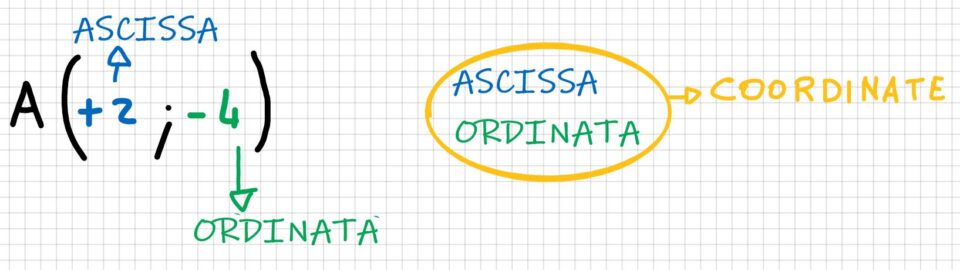
Per distinguere l’ascissa dall’ordinata, userò colori diversi. Quindi:
Inoltre dobbiamo ricordarci che il punto medio è quel punto che divide un segmento in due parti uguali.
Calcoliamo le coordinate
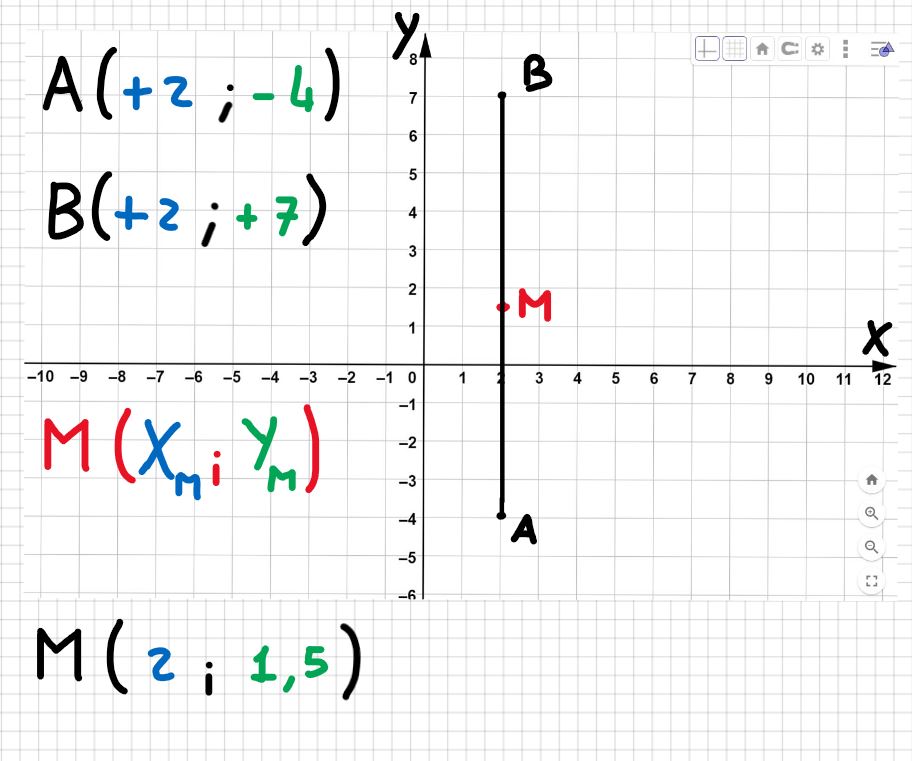
Ora che abbiamo le coordinate tracciamo il segmento sul piano cartesiano.
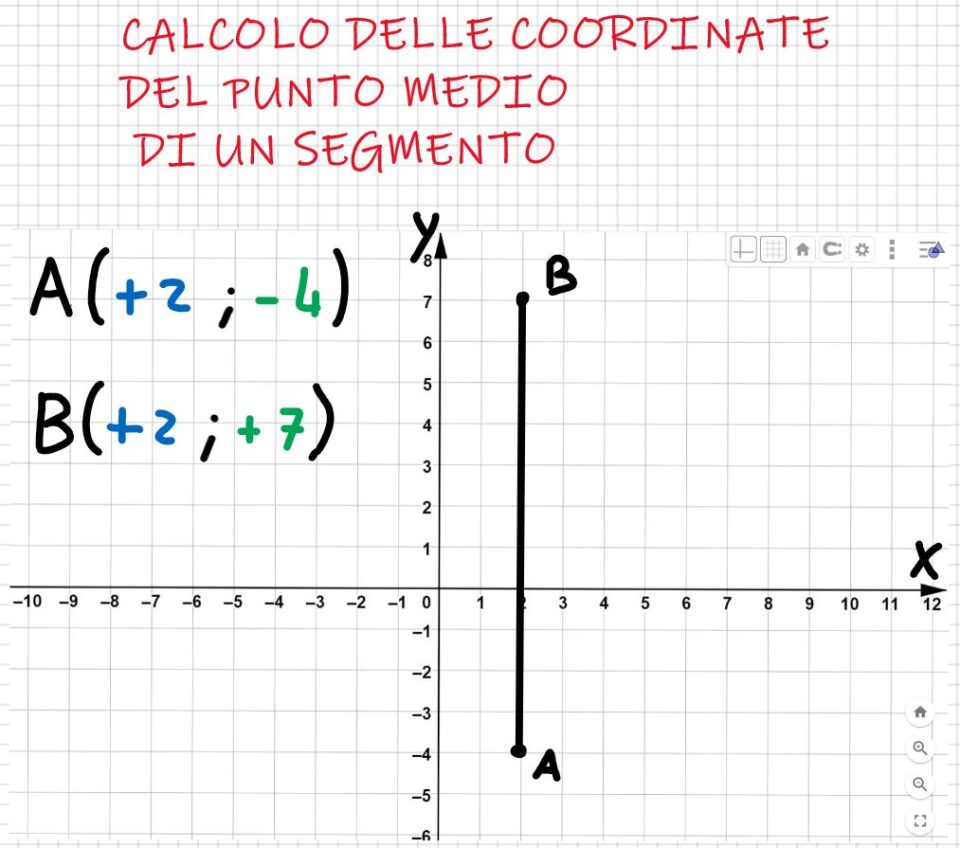
Per individuare il punto medio, si potrebbe operare graficamente, cioè andando a contare i quadratini e dividere il segmento in due parti uguali.
Ma noi le coordinate le dobbiamo calcolare, non determinarle guardando il grafico.
Come ogni punto, anche il punto medio sarà individuato da due numeri, cioè avrà due coordinate: l’ascissa e l’ordinata.
Chiamiamo il punto medio “M”.
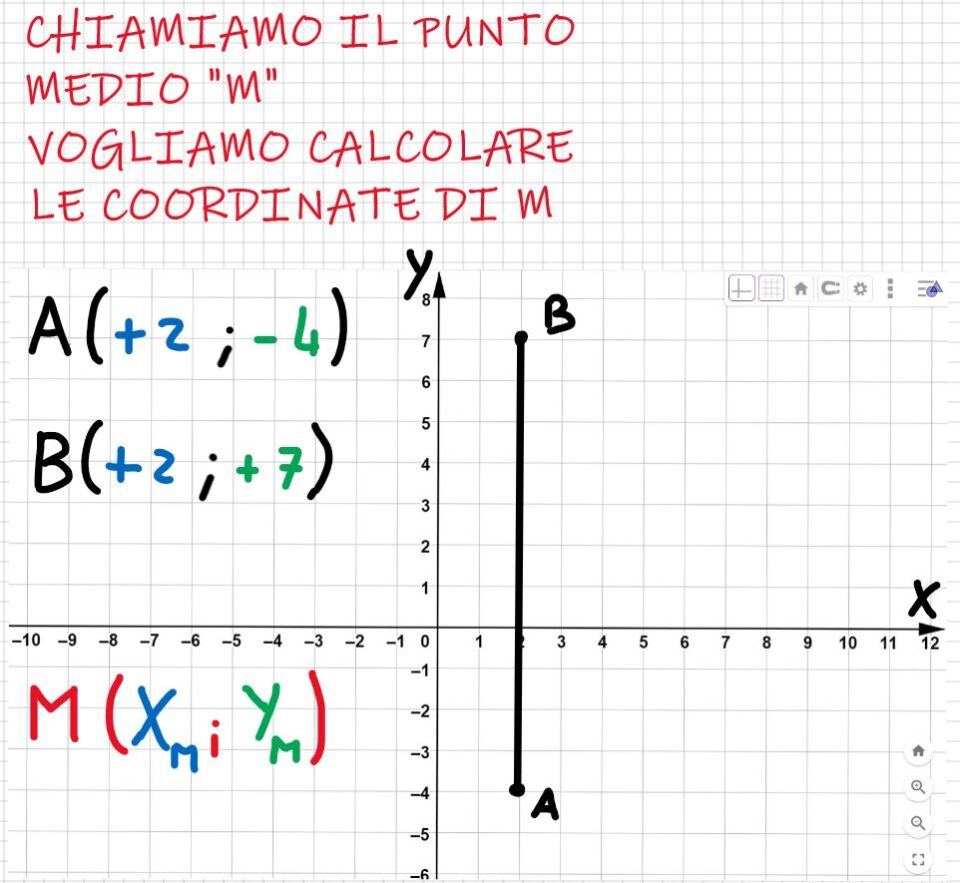
Ascissa del punto medio
Calcoliamo l’ascissa di M, cioè la XM. Quello che dobbiamo andare a fare è addizionare l’ascissa di A con l’ascissa di B e poi dividere il risultato per due. Passiamo ai numeri che è meglio.
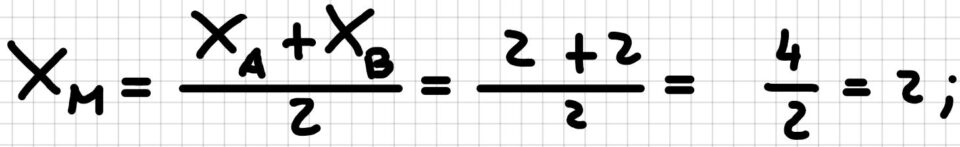
Il risultato che si ottiene è 2. Quindi l’ascissa del punto medio è 2.
Ordinata del punto medio
Dobbiamo andare a calcolare la seconda coordinata, cioè l’ordinata del punto M, in simboli YM.
Per ottenere la YM dobbiamo sommare la YA con la YB e dividere il risultato per 2.
Detta con parole difficili, bisogna fare la semisomma delle ordinate.
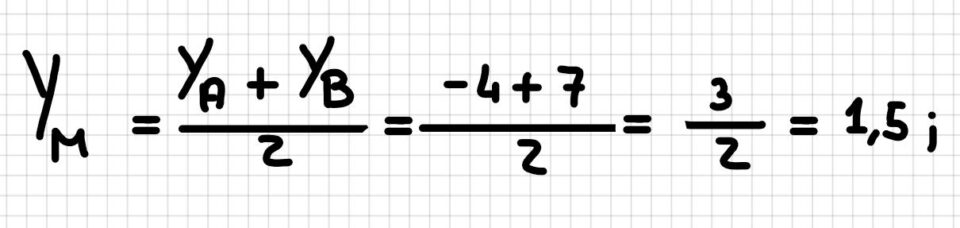
Se non ti ricordi come si esegue una somma tra numeri relativi potresti andare a dare un’occhiata al mio articolo somma tra numeri relativi.
Il risultato che otteniamo è +1,5.
Quindi ricapitolando il punto M ha coordinate (2 ; 1,5 ).

Ora ti sarà anche chiaro perché per separare le coordinate si usa il “;” e non la virgola. Infatti la virgola si potrebbe confondere con la virgola di un numero decimale.
Tracciamo il nostro punto sul grafico.
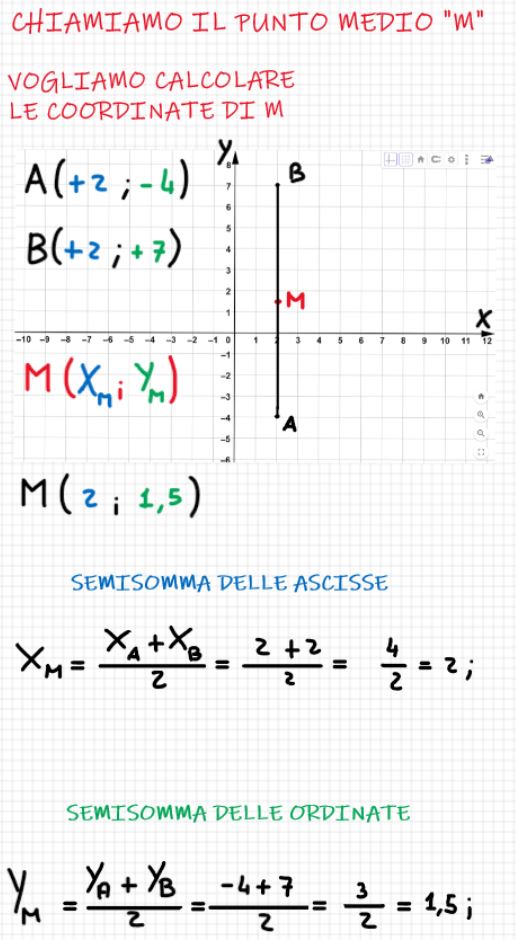
Riepilogo
Nell’immagine successiva hai uno sguardo d’insieme di quello che hai letto fino a ora.
Primo esercizio
Adesso se vuoi, puoi metterti alla prova con l’esercizio che leggi sotto. Lavora con calma e non ti preoccupare se sbagli. Sbagliando si impara. Se guardi bene, sotto il grafico, troverai le coordinate. Il risultato ti serve per capire se hai lavorato oppure no.
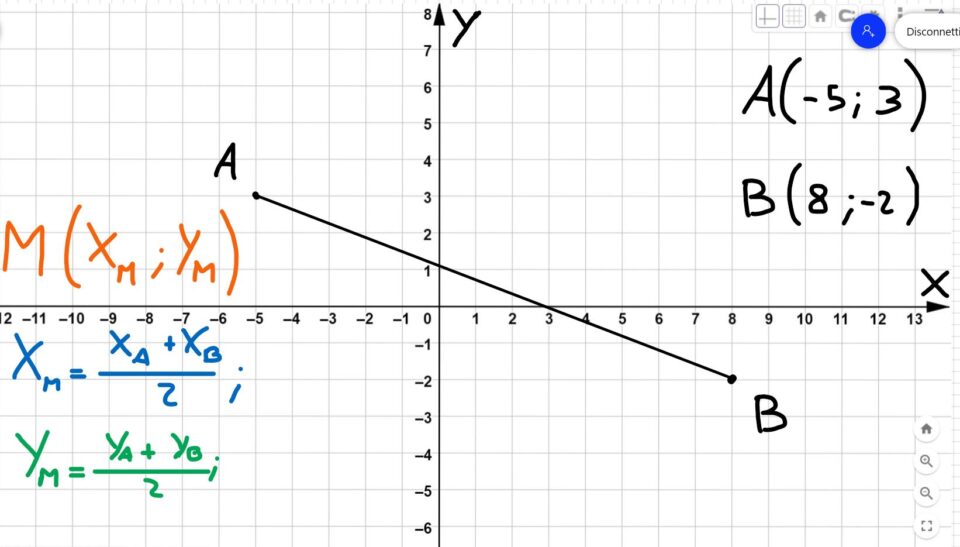
Il risultato è M(1,5; 0,5)
Secondo esercizio
Leggi con attenzione le consegne ed esegui l’esercizio proposto.
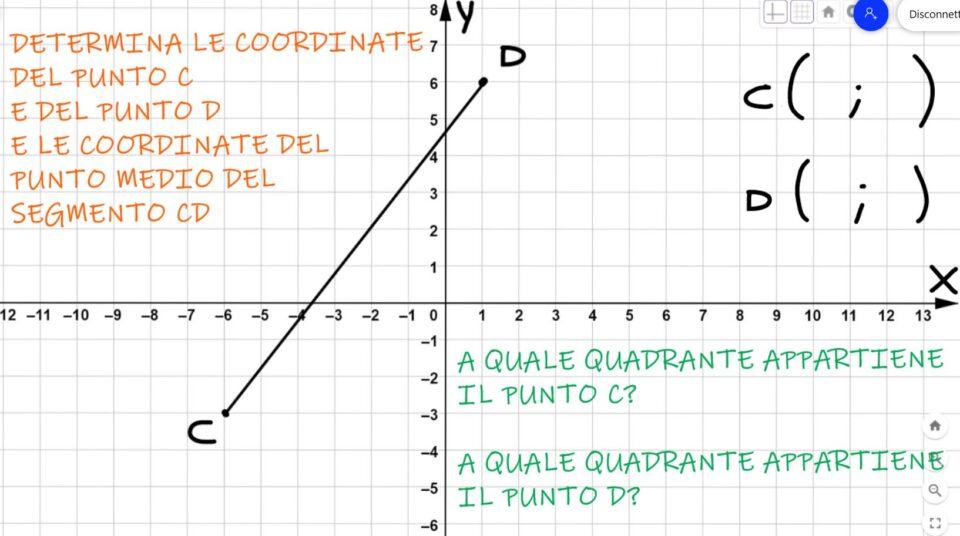
C( -6:-3) appartenente al III quadrante; D(1;6) appartenente al I (primo) quadrante; M(-2,5;1,5)
Le immagini che vedi nell’articolo sono state realizzate usando il software free Whiteboard della Microsoft e una tavoletta grafica One by Wacom.
Se vuoi porre domande o vuoi segnalre un errore puoi scrivere alla casella mail: matematica.facile@libero.it oppure puoi contattarci attraverso le nostre pagine social.