Vediamo un altro esercizio di divisione tra frazioni. Proviamo a calcolare sei tredicesimi fratto 2.
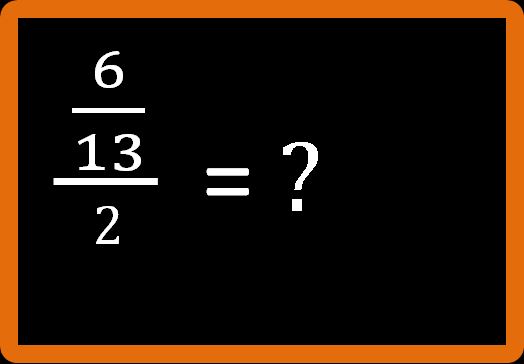
In questa frazione abbiamo al numeratore una frazione. Al denominatore invece abbiamo un numero naturale. Niente paura. I passaggi da eseguire sono gli stessi di quelli visti nell’ articolo in cui parlavo della divisione tra frazioni.
Dobbiamo moltiplicare la frazione al numeratore per l’inverso della frazione al denominatore. A questo punto starai pensando ‘ma al denominatore non abbiamo una frazione’. Ci arriveremo. Facciamo le cose una alla volta.
Passaggio 1
Come prima cosa riscriviamo la frazione al numeratore.
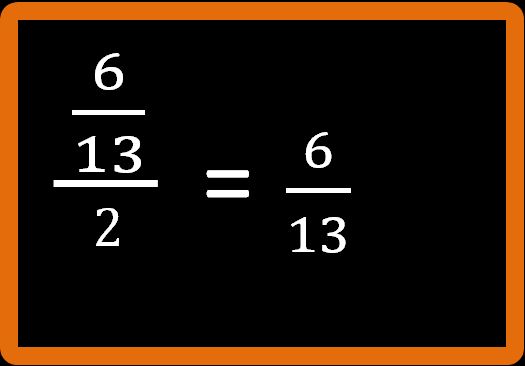
Passaggio 2
La seconda cosa da fare è scrivere il segno della moltiplicazione.
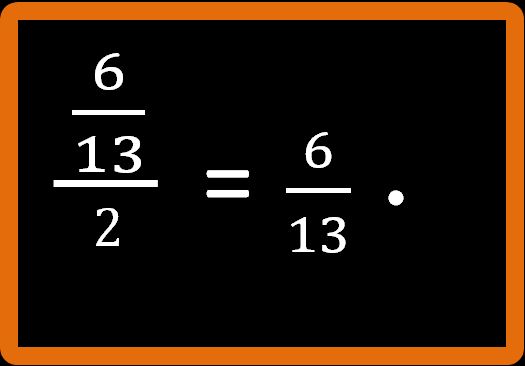
Adesso dovremmo scrivere l’inverso della frazione al denominatore. Ma al denominatore abbiamo 2, che è un numero naturale. Quindi come facciamo? Abbiamo già visto in altri articoli che tutti i numeri naturali (e quindi anche il numero 2) possono essere pensati come frazioni in cui il denominatore è 1.
Mi spiego meglio:
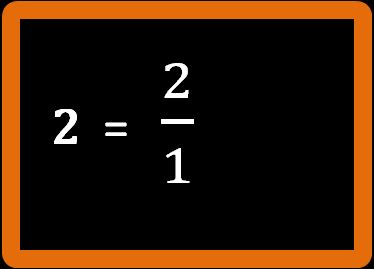
Questo non ci deve stupire. Ti ricordo che una frazione non è altro che una divisione scritta in modo diverso. Scrivere 2 fratto 1 è come 2 : 1. E sappiamo che 2 : 1 = 2.
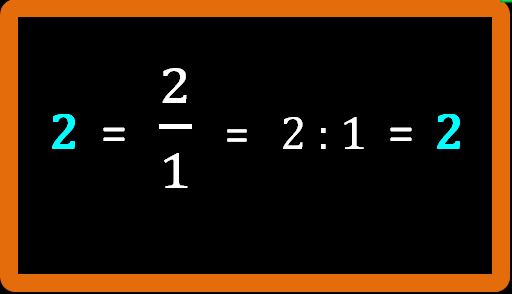
Ritorniamo alla nostra frazione. La frazione inversa di due fratto uno è uno fratto due che si può anche leggere un mezzo non un secondo.

Bene, adesso che abbiamo ricavato la frazione inversa, possiamo continuare.
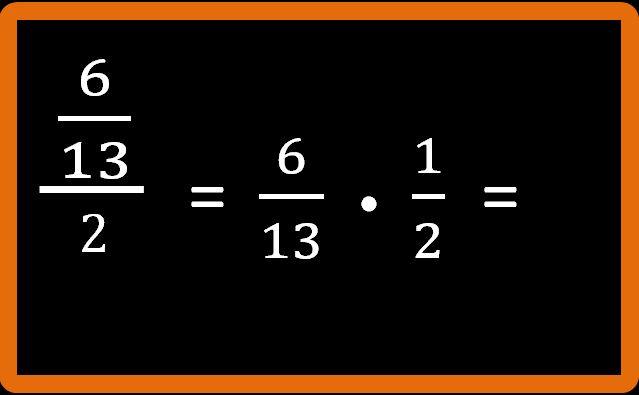
Passaggio 3
Adesso dobbiamo semplificare in croce. Dividiamo per 2 sia il 6 al numeratore della prima frazione sia il 2 al denominatore della seconda frazione.
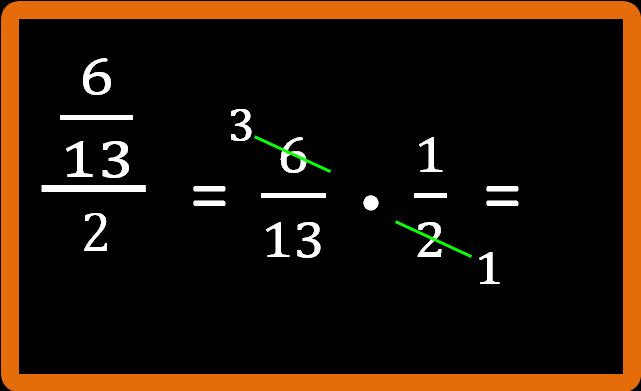
Passaggio 4
Adesso che non è più possibile semplificare, non ci resta che moltiplicare.
Numeratore per numeratore, cioè 3 · 1 = 3.
Denominatore per denominatore, cioè 13 · 1 = 13.
Quello che otteniamo è:
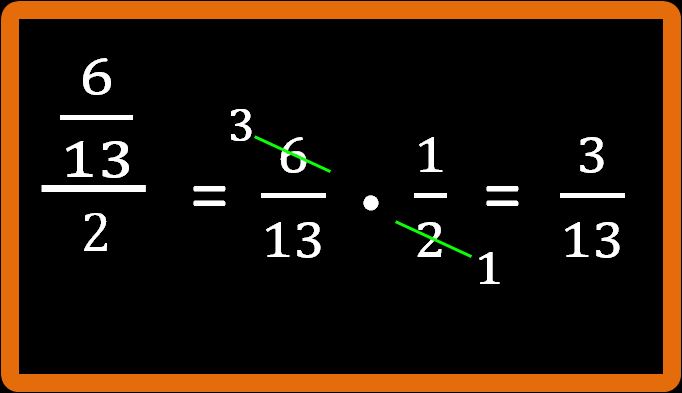
Fantastico. Tre tredicesimi è il risultato che stavamo cercando. Esercizio concluso.
Link utili
A questo link della Casa Editrice Zanichelli puoi trovare le tavole numeriche. Le puoi consultare o scaricare come file pdf.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.