In questo articolo vedremo un esercizio svolto di espressione con radici e frazioni. Vedere come si esegue un esercizio ti può essere utile per sapere eseguire anche tutti gli altri esercizi. Quindi meglio finirla con le parole e cominciamo subito con un esempio numerico.
esempio svolto
Cominciamo con l’esempio che vedi nella lavagna sotto.
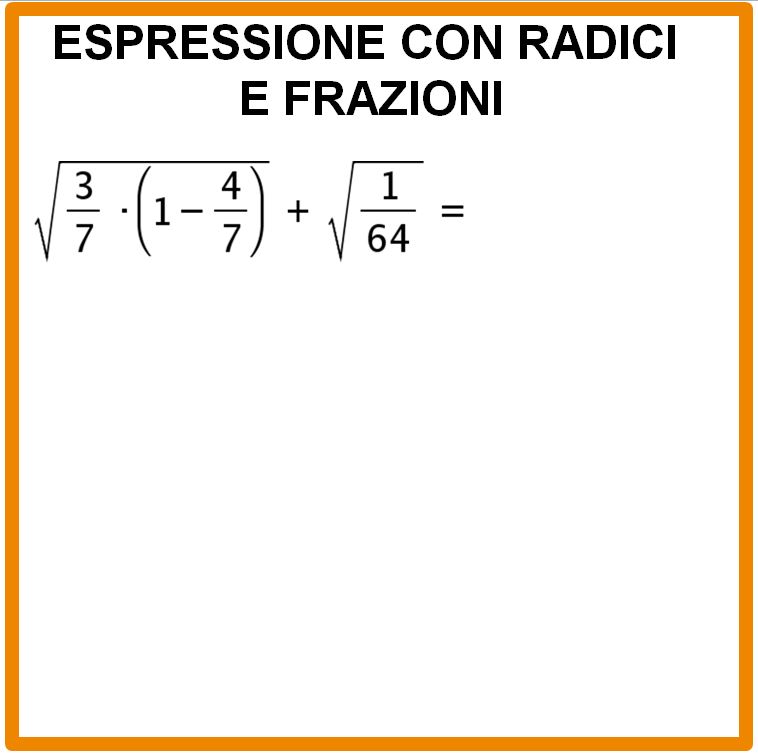
Dobbiamo procedere rispettando alcune precedenze. Se vuoi ripassare le precedenze, potresti dare un’occhiata al mio articolo espressioni con le radici. Le operazioni da eseguire sono quelle all’interno della parentesi tonda e poi possiamo estrarre la seconda radice quadrata. Per essere più chiari tracciamo una linea di colore verde sotto le operazioni che andiamo a eseguire.
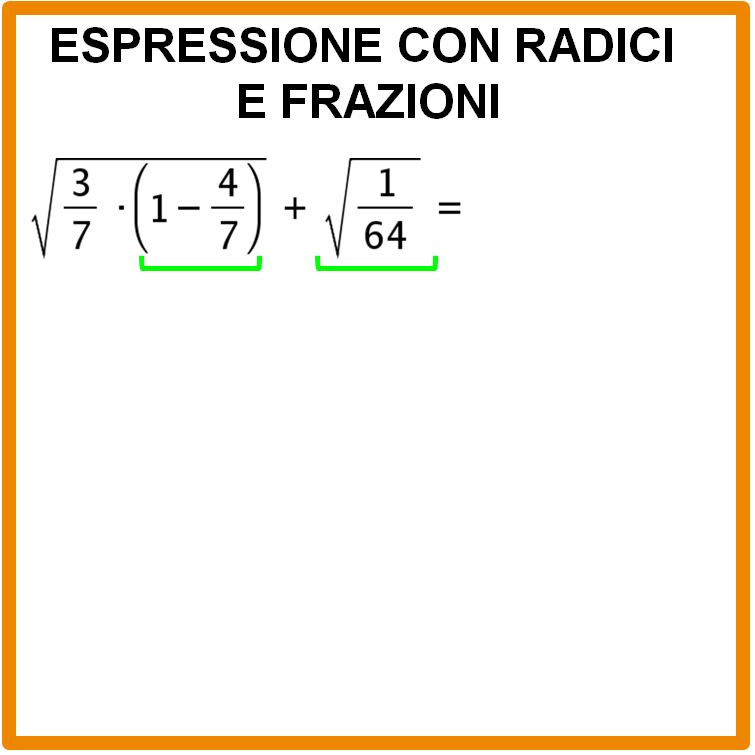
All’interno della parentesi tonda abbiamo una sottrazione tra un numero naturale: 1 e una frazione: quattro settimi. Se vuoi rivedere come si esegue un’operazione del genere, puoi leggere il mio articolo: sottrazione tra frazioni.
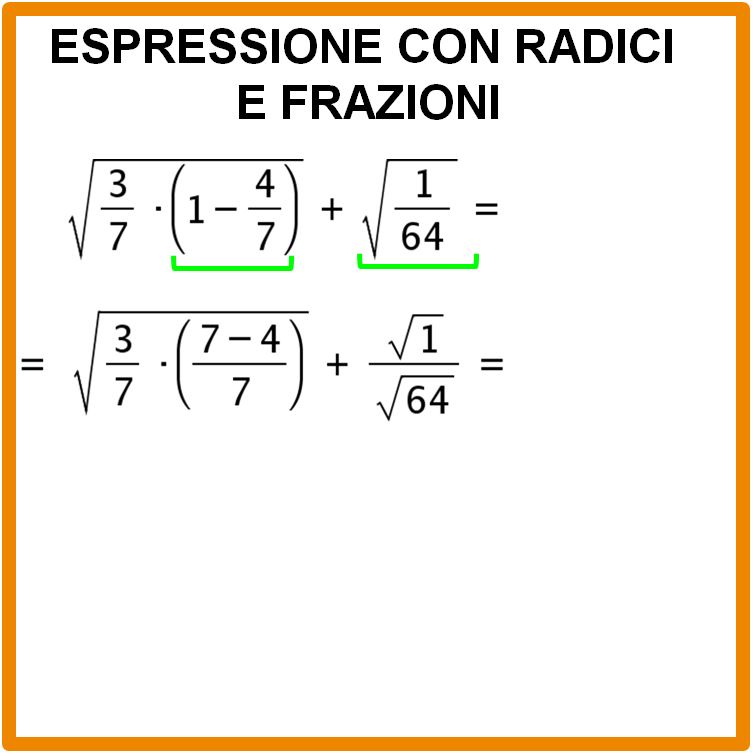
Per quanto riguarda la seconda radice, ci conviene applicare una delle proprietà delle potenze. La proprietà che ci interessa dice che:
“La radice di un quoziente è uguale al quoziente delle radici”.
Se guardiamo la lavagna in basso capiremo meglio cosa vuol dire.
Andiamo avanti eseguendo la sottrazione che compare all’interno della parentesi al numeratore ed estraiamo anche le radici alla fine dell’espressione:
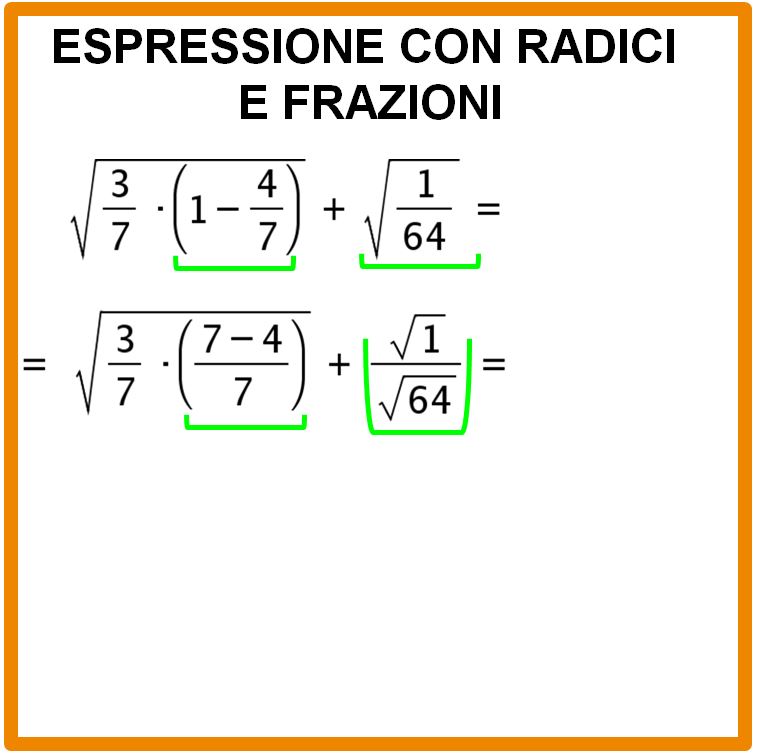
I risultati che otteniamo sono visibili nella lavagna in basso.
- La radice quadrata di 1 è 1 perchè 1 · 1 = 1 in modo simile
- la radice quadrata di 64 è 8 perchè 8 · 8 = 64.
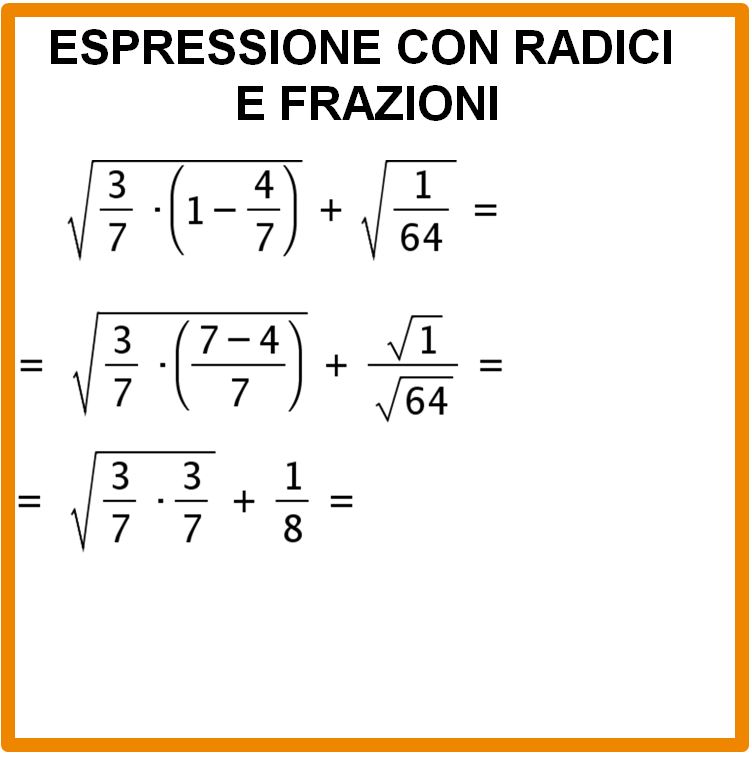
Bene. Procediamo con la nostra espressione con radici e frazioni eseguendo le operazioni sotto radice.
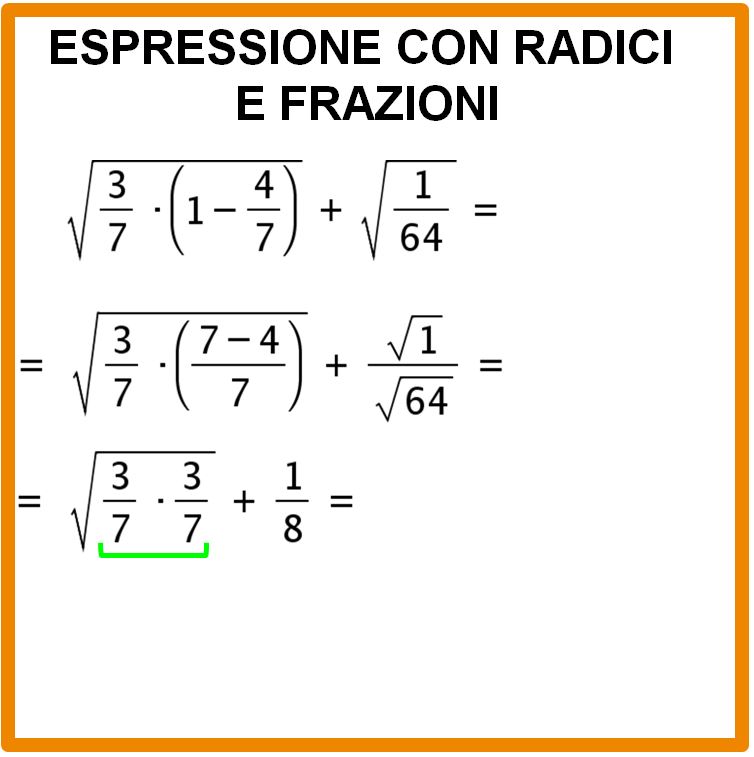
Eseguiamo la moltiplicazione tra frazioni. Se non ti ricordi come si esegue potresti leggere l’articolo: moltiplicazione tra frazioni. Il risultato che otteniamo lo leggiamo sotto.
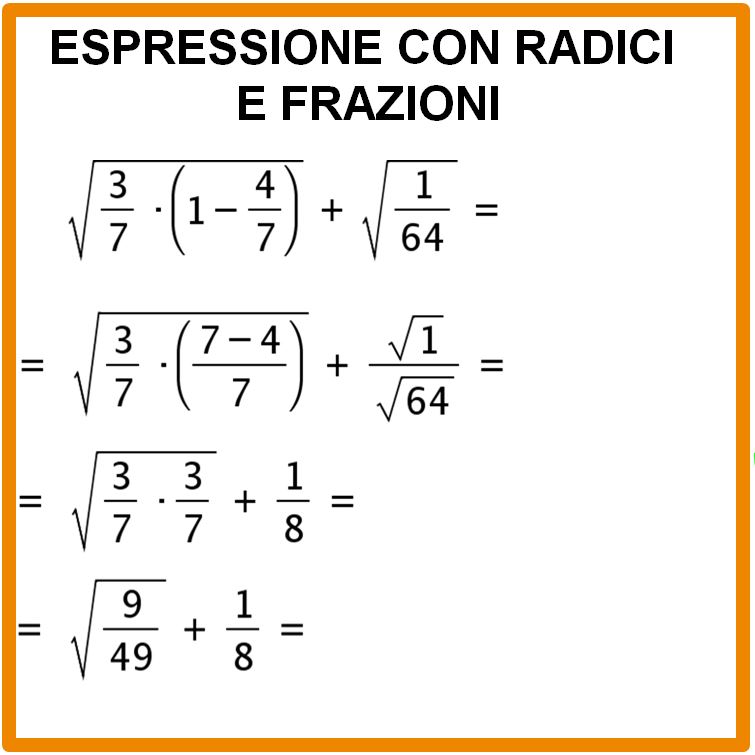
Adesso estraimo la radice della frazione sotto radice, applicando la proprietà delle radici che abbiamo già visto in uno dei passaggi precedenti (la radice di un quozionete è uguale al quoziente delle radici).

- La radice quadrata di 9 è 3 perchè 3 · 3 = 9 e analogamente,
- la radice quadrata di 49 è 7 perchè 7 · 7 = 49.

Ci siamo liberati delle radici. Non ci resta che eseguire la somma tra due frazoni con denominatore diverso tre settimi e un ottavo.

Ora eseguiamo la somma che compare al numeratore.

Abbiamo concluso. Il risultato che stavamo cercando è trentuno cinquantaseiesimi.
Cliccando qui si aprirà una nuova pagina in cui potra scaricare gratuitamente le tavole numeriche.
Se hai delle domande o vuoi segnalare un errore, puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori.