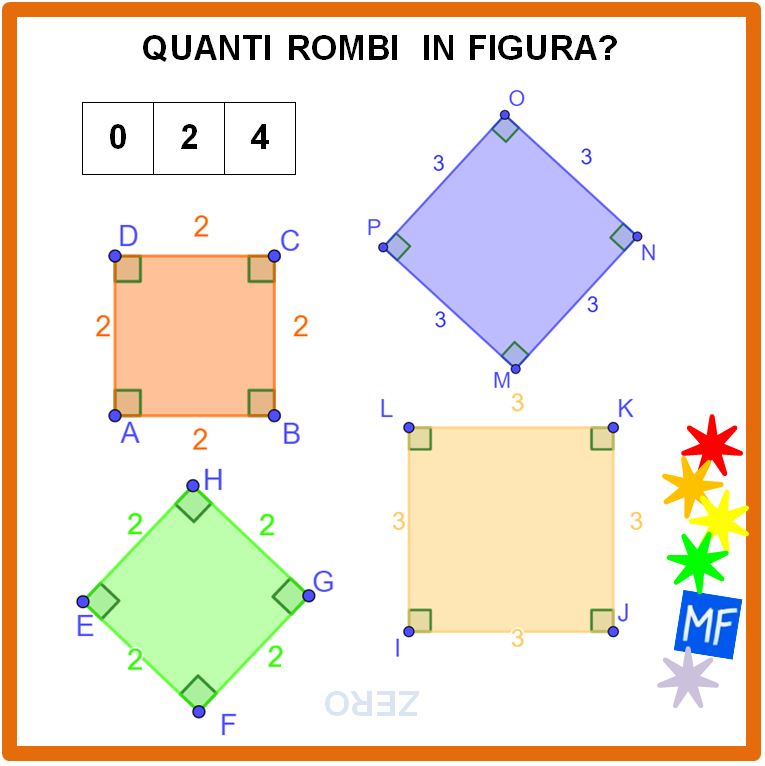
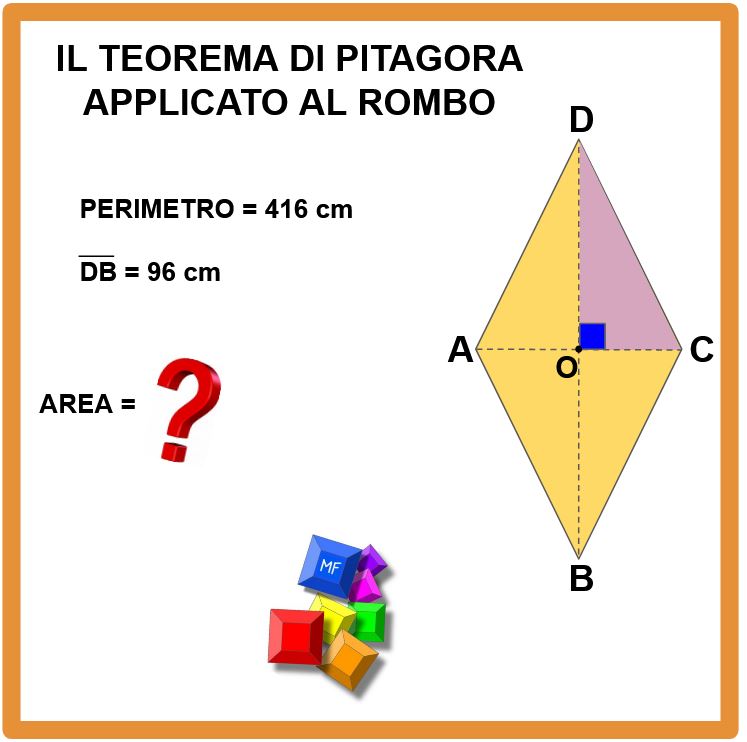
Dopo avere visto come distinguere un rettangolo da un parallelogramma, passiamo ora all’applicazione delle formule dirette e inverse del rettangolo che ci permetteranno di calcolare la lunghezza delle dimensioni (base e altezza), il perimetro e l’area di questo quadrilatero.
Indice
Iscriviti al mio canale Youtube
Concetti da ricordare
Prima di cominciare è meglio ripassare velocemente alcuni concetti:
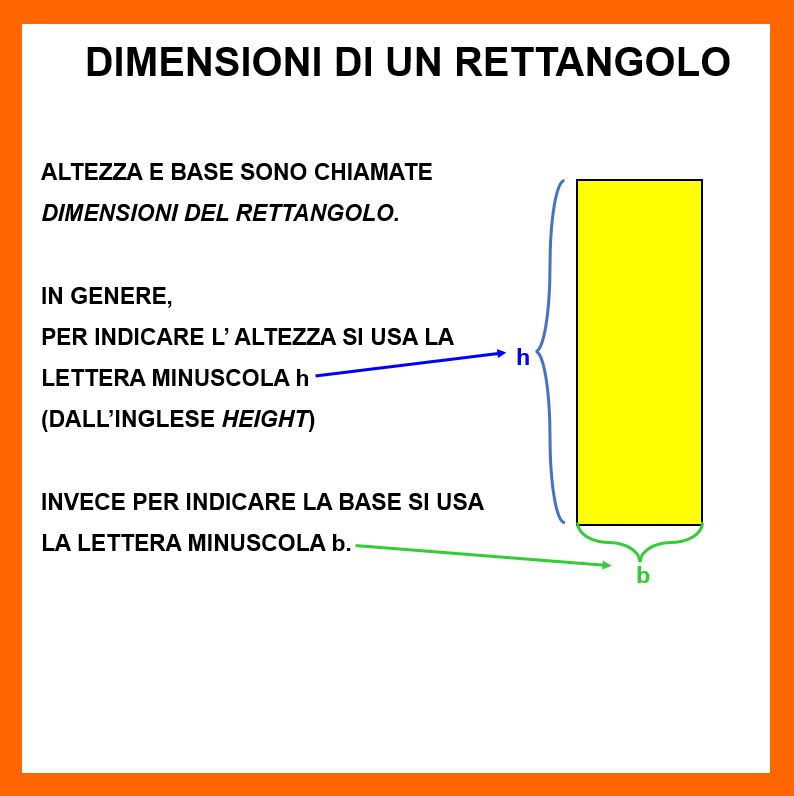
- le dimensioni di un rettangolo sono: base e altezza;
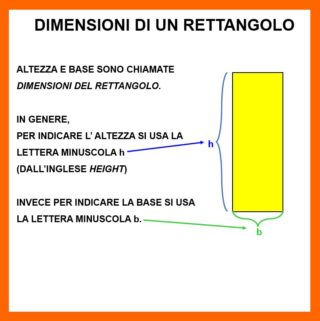
Normalmente si sceglie come base il lato “orizzaontale”, ma si può scegliere come base uno qualsiasi dei 4 lati. Come vedi nella figura in basso.
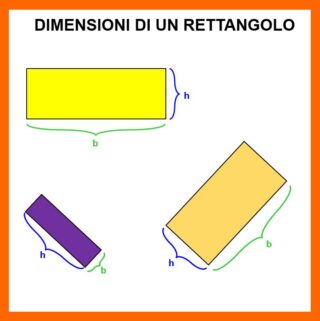
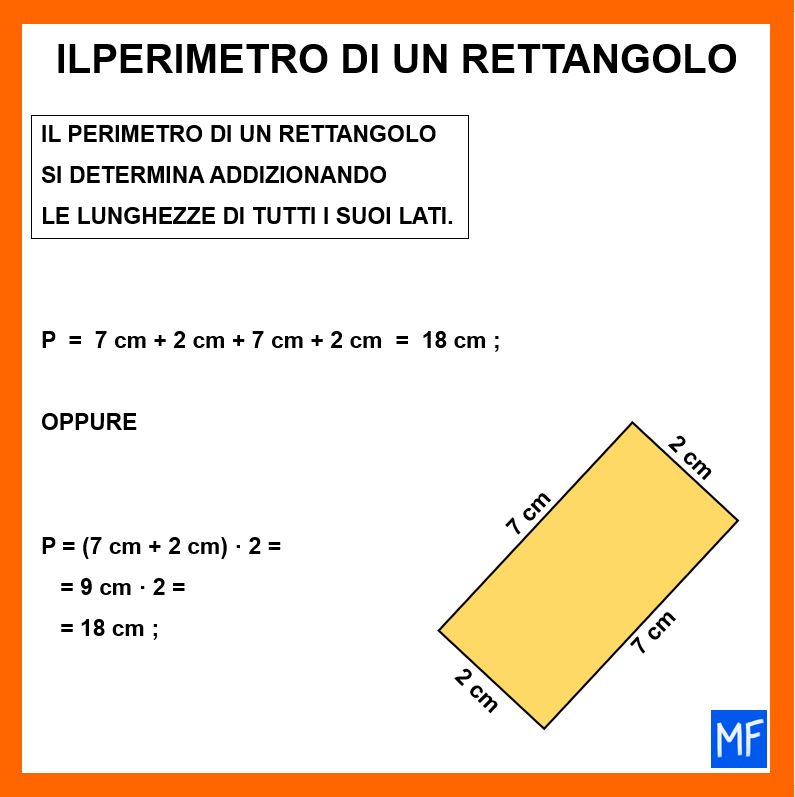
- il perimetro si determina addizionando la lunghezza di tutti i i lati (come in ogni poligono);
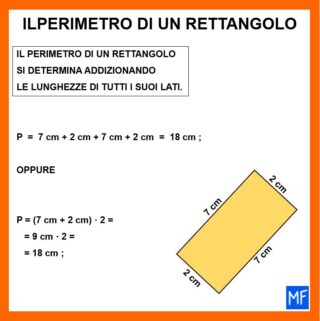
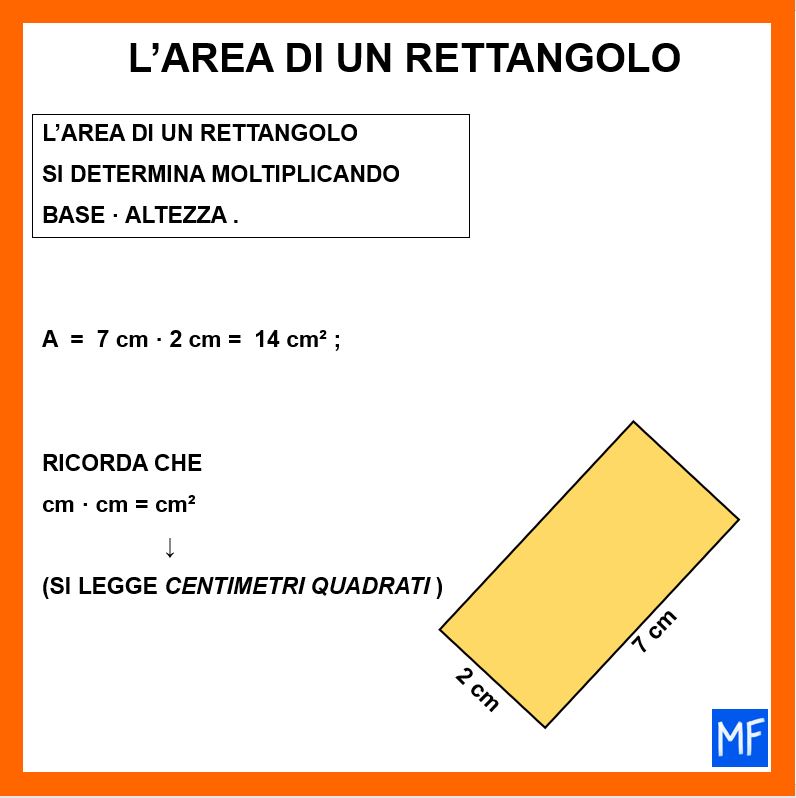
- l’area si trova moltiplicando la base per l’altezza.
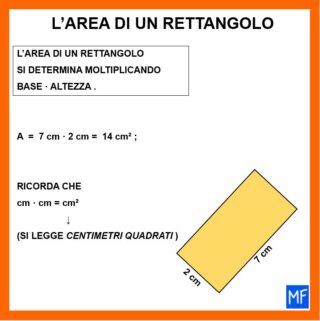
Breve riassunto
Le tre figure in basso riassumono quello che abbiamo detto finora.
Primo esempio: il campo da tennis
Cominciamo con qualche esempio con i numeri. Partiremo da cose semplici e poi eseguiremo esercizi più difficili. Prima impareremo a camminare e poi a correre.
Guardiamo la lavagna e con i dati a nostra disposizione cerchiamo di determinare la supeficie (in altre parole l’area) del campo da tennis (le dimensioni sono molto simili a quelle reali).


Applichiamo la formula
A = b · h
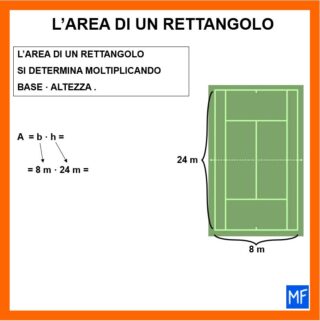
Non ci rimane che eseguire la moltilicazione.
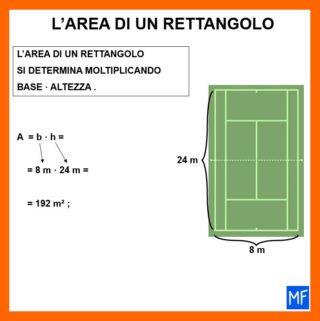
Il risultato che stavamo cercando è 192 m² (si legge 192 metri quadrati oppure 192 metri alla seconda).
Secondo esempio: la piscina
Facciamo un altro esempio per applicare le formule dirette e inverse del rettangolo. Calcoliamo la lunghezza di una piscina olimpionica. Della piscina conosciamo la sua superficie e la sua larghezza.

In questo esempio useremo lunghezza e larghezza, invece di usare altezza e base. Ma le formule sono le stesse. Nel linguaggio usato comunemente, si usano spesso lunghezza e larghezza quando si parla di rettangoli.
Il campo da tennis dell’esempio precedente era lungo 24 metri. Bene, ora vogliamo capire quanto è lunga una piscina olimpionica (cioè una piscina come quella usata durante le Olimpiadi).

Andiamo ai calcoli, sappiamo che la superficie della piscina misura 1250 m² e sappiamo anche che la piscina è larga 25 metri.

La formula che ci permette di calcolare la lunghezza della piscina l’abbiamo vista nell’immagine precedente.

Andiamo a sostituire con i valori che abbiamo. Facciamo attenzione alle unità di misura.

Il risultato che abbiamo trovato è 50 metri. Questo vuol dire che una piscina olimpionica è lunga 50 metri. Chi va in piscina saprà che si dice “una vasca” è lunga 50 m.
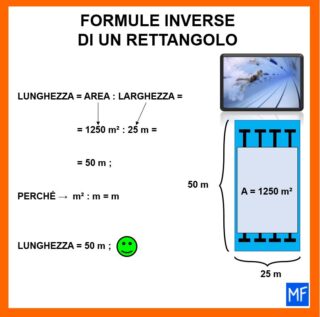
Le formule
Nell’immagine in basso sono mostrate le formule che permettono di ricavare una delle dimensioni di un rettangolo, conoscendo l’area e l’altra dimensione.

Terzo esempio: la casetta
Guardiamo la lavagna in basso e cerchiamo di ricavare il dato mancante usando ciò che sappiamo.
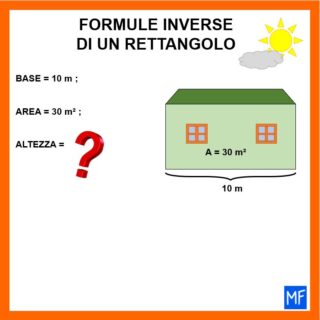
Dobbiamo calcolare l’altezza della casetta. La formula che dobbiamo applicare è:
h = A : b
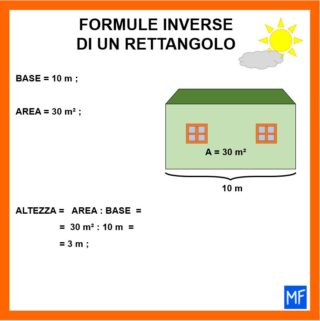
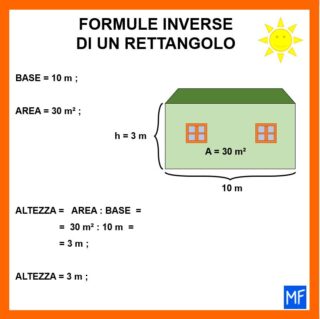
Applicando la formula corretta ed eseguendo i calcoli, troviamo che la casetta è alta 3 m.
Esercizi
Se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf in basso. Buon lavoro.
![]() Il rettangolo: formule dirette e inverse; esercizi.pdf
Il rettangolo: formule dirette e inverse; esercizi.pdf
Se hai perso le tavole numeriche puoi scaricarle gratuitamente in questa pagina della Casa Editrice Zanichelli.
Se vuoi segnalare un errore o vuoi porre delle domande puoi raggiungerci attraverso le nostre pagine social oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.