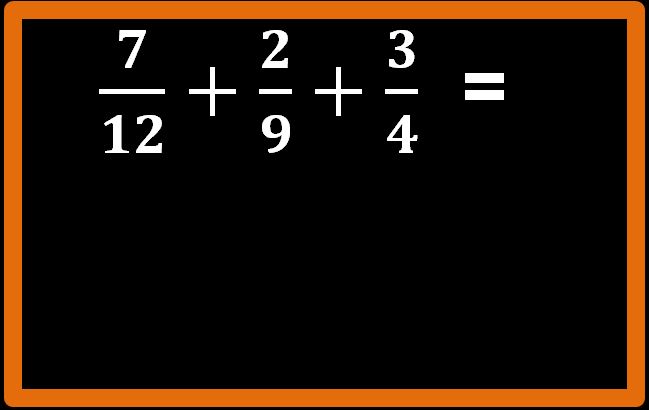Cos’è il minimo comune multiplo
Ok, se sei finito qui è perchè il minimo comune multiplo proprio non riesci a capirlo. Ma prima di cominciare, una piccola premessa. Alcuni libri lo abbreviano con M.C.M., altri invece con m.c.m., non fa nessuna differenza, sono due modi diversi di scrivere la stessa cosa. Il consiglio che posso darti è quello di seguire il modo che usa la tuo prof.
Passiamo ai calcoli. Ho una notizia buona e una cattiva. La notizia buona è che con dieci minuti di impegno riuscirai a calcolare l’ m.c.m. tra due o più numeri qualsiasi.
La notizia cattiva è che per calcolare l’ m.c.m. devi ripassare prima un paio di concetti come la scomposizione in fattori primi e i numeri primi.
Vedi, saper calcolare il minimo comune multiplo è come voler costruire il terzo piano di una casa. Ma prima devi aver costruito il primo e il secondo piano. Se non ricordi come si scompongono i numeri in fattori primi potresti dare un’occhiata al mio articolo: la scomposizione in fattori primi. Se invece vuoi ripassare quali sono i numeri primi puoi visitare questa pagina: i numeri primi.
Dopo aver letto i primi paragrafi forse ti starai chiedendo a cosa serve saper calcolare l’m.c.m.. Il minimo comune multiplo è un argomento che ritroverai spesso durante la tua carriera scolastica, ad esempio quando studierai la somma e la differenza tra frazioni con denominatore diverso e forse potrà tornarti utile anche nel Test INVALSI.
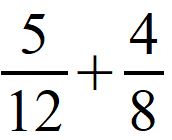
Per eseguire questa somma tra frazioni devi sapere calcolare il minimo comune multiplo tra i denominatori
Indice
- Cosa significa minimo comune multiplo
- Esempio con i numeri
- Calcoliamo l’m.c.m.
- Scelta dei fattori
- Casi particolari
- Altri esempi
- Minimo comune multiplo tra 3 numeri
- Massimo comune divisore (M.C.D.)
- Esercizi in pdf
- Link utili
Cosa significa minimo comune multiplo
Armiamoci di pazienza e di impegno e iniziamo a fare sul serio. Cominciamo dando un’occhiata al nome: minimo comune multiplo. So che ti può sembrare banale, ma cerchiamo di capire cosa significano le parole prese una alla volta.
Minimo : minimo vuol dire più piccolo. Se io ti chiedessi: “Qual è il minimo tra 5, 24, 11 e 3 ?” La risposta corretta è 3, perchè è il più piccolo tra i numeri elencati. Detto in modo diverso 3 è il minimo tra i numeri che ti ho dato. Facciamo un altro esempio solo per essere sicuri di avere capito. Qual è il minimo tra 23, 17, 20 e 22 ? La risposta corretta è 17. Bene, andiamo avanti.
Comune : qualcosa si dice in comune se appartiene a più persone o a più cose. Facciamo un esempio. Cosa hanno in comune le due moltiplicazioni 5×8 e 3×8 ? In tutte e due compare il fattore 8. Oppure ancora cosa hanno in comune i numeri 12, 22, e 32? Alcune risposte corrette potrebbero essere: tutti finiscono con il 2 e sono tutti numeri pari.
Multiplo : sono sicuro che hai già sentito parlare dei multipli. Passiamo subito a qualche esempio numerico. Quali sono i multipli di 2? La risposta è : 2, 4, 6, 8, 10 e via elencando. Quali sono i multipli di 6? 6, 12, 18, 24, 30, 36 e via discorrendo, in altre parole la tabellina del 6.
Esempio con i numeri
Finalmente dopo avere visto il significato delle singole parole, possiamo metterle assieme. Facciamo un esempio con i numeri e cerchiamo di capire qual è l’ m.c.m. tra 4 e 6. Cominciamo scrivendo i multipli di 4, non tutti naturalmente.
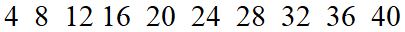
Bene, fatto questo, scriviamo i multipli del numero 6.
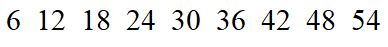
Fantastico, adesso disegnamo un cerchio attorno i numeri che sono sia multipli di 4 sia multipli di 6.
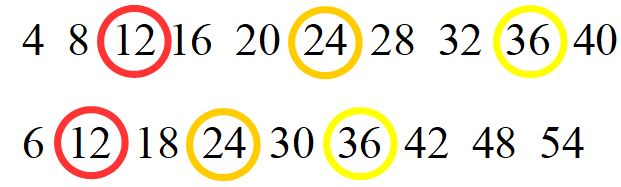
Dando un’occhiata e cercando con un po’ di attenzione ci accorgiamo che i numeri che sono sia multipli di 4 che multipli di 6 sono: 12, 24 e 36. (Naturalmente ce ne saranno anche altri, ma a noi non piace lavorare con numeri troppo grandi e poi in questo momento non è necessario). Hai appena trovato i multipli comuni, cioè i multipli che sono in comune tra il numero 4 e il numero 6.
Ma a noi non interessano tutti i multipli, noi stiamo cercando di trovare il più piccolo, il minimo. E qual è il numero più piccolo tra 12, 24 e 36? La risposta è 12.

Hai appena trovato il minimo comune multiplo tra 4 e 6.
Prima di andare avanti facciamo un altro esempio. Proviamo a determinare l’m.c.m. tra 3 e 4. Seguiamo lo stesso procedimento. Scriviamo quindi prima i multipli di 3 (non tutti) e poi i multipli di 4 (non tutti).

Come abbiamo fatto prima, evidenziamo con un cerchio i multipli comuni, cioè i numeri che sono sia multipli di 3, sia multipli di 4:
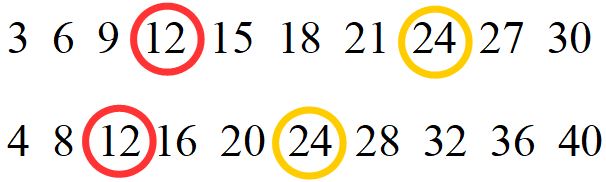
Benissimo, ora ci manca solo l’ultimo passaggio, cioè stabilire qual è il più piccolo dei multipli comuni. Come avrai già capito è 12. Quindi 12 è il minimo comune multiplo tra i numeri 3 e 4.
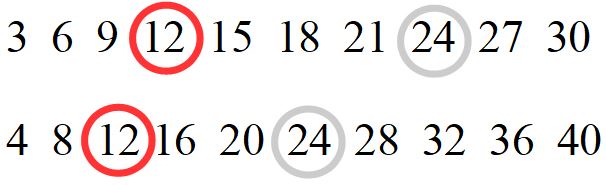
12 è l’m.c.m.. Facile no?
Calcoliamo l’m.c.m.
Ora che abbiamo ben chiaro cosa vuol dire m.c.m., passiamo a qualcosa di leggermente più complicato. Come hai visto fino ad ora abbiamo lavorato solo con numeri piccoli, ma come si procede se per esempio voglio ottenere l’m.c.m. tra 18 e 30? Non possiamo seguire il metodo adottato fino a questo punto, perchè pur essendo corretto non è facilmente praticabile con numeri grandi. Dovremmo infatti scrivere i multipli di 18 e 30, con la possibilità di sbagliare.
Per esempio, proviamo a scrivere i primi cinque multipli di 18:
18, 36, mmm 54, mmmmm.
No, non è una strada praticabile. Devi tenere presente che avrai a che fare anche con numeri più grandi e magari più complicati.
Per calcolare l’m.c.m. tra 18 e 30 (ma vale lo stesso per qualsiasi coppia di numeri) è necessario scomporli in fattori primi.
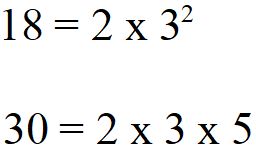
Scomposizione in fattori primi e scrittura esponenziale di 18 e 30
Vediamo come si procede. Leggerai ora una frase che hai sentito sicuramente in classe, ma è un po’ tenebrosa: “Per calcolare l’ m.c.m. bisogna moltiplicare i fattori comuni e non comuni presi una volta con il maggiore esponente“. Vediamo di capire cosa vuol dire.
Ti ricordo che in matematica i fattori sono gli elementi della moltiplicazione. Quindi nel nostro esempio i fattori sono 2, 3 e 5. Il 2 e il 3 sono fattori comuni a tutte e due le scomposizioni, quindi sono fattori comuni, mentre il 5 compare solo nella scomposizione del 30. Il 5 è un fattore non comune.
L’esponente, nel caso in cui non ti ricordi cosa sia, è quel numerino scritto in alto a destra del numero. Nel nostro esempio solo il 3, nella scomposizione del 18, presenta un esponente che è 2 (ti ricordo che si legge 3 elevato alla seconda oppure 3 alla seconda oppure 3 al quadrato): 32.
Bene, una volta chiariti questi concetti non ci resta che scegliere i fattori per calcolare l’ m.c.m. tra 18 e 30.
Scelta dei fattori
Il fattore 2 compare sia nella prima che nella seconda scomposizione e in tutte e due ha lo stesso esponente. So cosa stai pensando: ‘non c’è nessun numerino in alto a destra del due’. È vero, infatti in questo caso l’esponente è 1, cioè sarebbe 21 , ma il numero 1 come come esponente non si scrive mai. Torniamo alla nostra scelta, abbiamo detto che il numero 2 compare sia nella prima che nella seconda scomposizione con lo stesso esponente, quindi possiamo scegliere quello che più ci piace. Ma attenzione solo uno dei due, non tutti e due. Ti ricordi la frase ‘presi una sola volta‘ è questo che vuol dire.
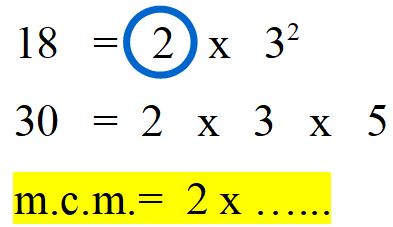
Il 2 è il primo fattore scelto
Avresti anche potuto scegliere il 2 che compare nella scomposizione del 30. Il risultato non sarebbe cambiato e il procedimento è sempre esatto.
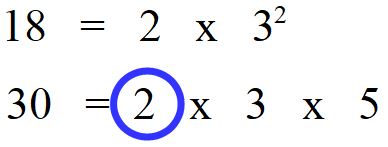
Vediamo quali altri fattori dobbiamo scegliere. Concentriamoci sul 3. Il numero 3 è presente sia nella prima che nella seconda scomposizione, però presenta esponenti diversi. Infatti nella prima scomposizione ha esponente 2 (32), mentre nella seconda scomposizione ha esponente 1 (31 cioè 3). La regola dice che dobbiamo scegliere il fattore che ha esponente maggiore. Quindi la nostra scelta ricade sul 32 .
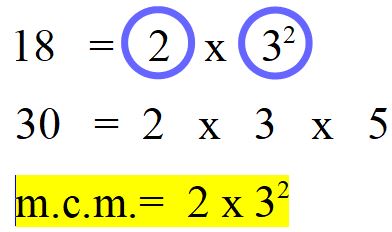
il 32 è il secondo fattore scelto per il calcolo dell’ m.c.m.
Vediamo se c’è da scegliere qualcos’altro. Siccome la regola dice che devono essere considerati i fattori comuni e non comuni, dobbiamo anche scegliere il 5 che compare nella scomposizione del 30. Il 5 sarà l’ultimo fattore grazie al quale calcoleremo l’m.c.m.
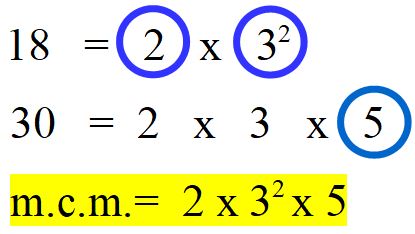
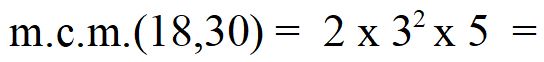
Ora non ci resta che moltiplicare tra loro i fattori che abbiamo scelto e avremo ottenuto l’ m.c.m. tra 18 e 30.
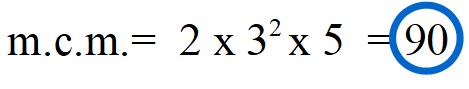
90 è il risultato che stavamo cercando.
Ti ricordo ancora una volta che avresti anche potuto scegliere l’altro 2, tanto hanno lo stesso esponente.
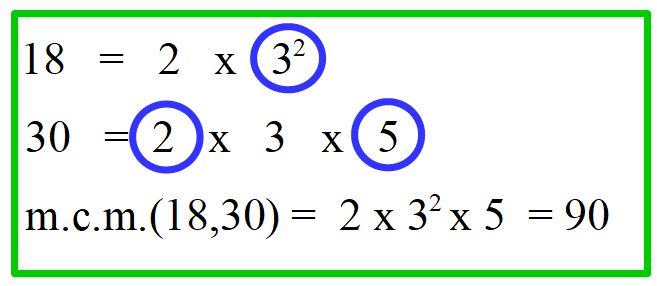
Procedimento corretto
L’importante è non sceglierli tutti e due. Questo è un errore molto comune. Ricordiamo la regola che dice ‘Per calcolare l’ m.c.m. bisogna moltiplicare i fattori comuni e non comuni presi una volta con il maggiore esponente ‘
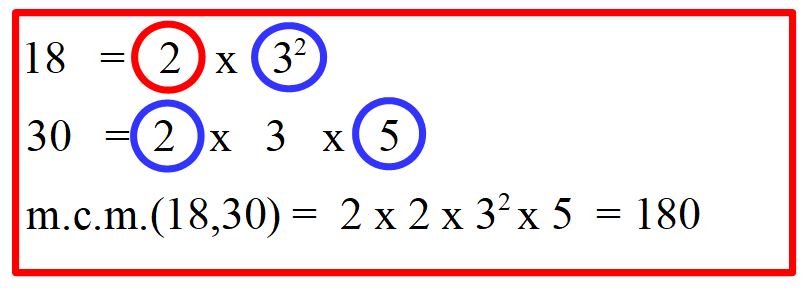
Procedimento scorretto che porta a ottenere un risultato scorretto
Bene, come abbiamo visto nel nostro esempio, abbiamo ottenuto come m.c.m. 90. Non devi preoccuparti se come m.c.m. ottieni un numero grande. Infatti l’m.c.m. tra due numeri sarà sempre più grande dei due numeri considerati (in realtà questo non è sempre vero, infatti esistono alcuni casi particolari che puoi trovare cliccando il link che trovi subito sotto).
Esercizi in pdf
Adesso possiedi gli strumenti necessari per calcolare il minimo comune multiplo tra due numeri qualsiasi (il procedimento è lo stesso anche se i numeri sono più di 2). Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf subito sotto. Puoi semplicemente visualizzarli oppure stamparli. Buon lavoro.
![]() Il minimo comune multiplo – Esercizi.pdf
Il minimo comune multiplo – Esercizi.pdf
Link utili
Cliccando qui visiterai il sito ufficiale dell’ Istituto INVALSI dove potrai trovare tutte le prove degli anni scorsi.
A noi interessano quelle di matematica formato CBT (Computer Based Test), ti ricordo infatti che la terza classe delle medie sosterrà la prova usando il computer, niente prova cartacea quindi.
A questo link della Casa Editrice Zanichelli trovi le Tavole Numeriche. Puoi semplicemente visualizzarle oppure anche scaricarle sotto forma di file pdf facendo click sull’icona che trovi in alto a destra nella pagina.
E poi selezionando Salva file e facendo click su OK.
Il file sarà scaricato nel tuo pc. Lo potrai trovare nella cartella Download. Da lì puoi tagliarlo e incollarlo dove ritieni opportuno, magari in una cartella in cui conservi tutte i file riguardanti la matematica.
Se hai dubbi o vuoi segnalare un errore puoi lasciare un commento oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che ci segnaleranno eventuali errori presenti nell’articolo.