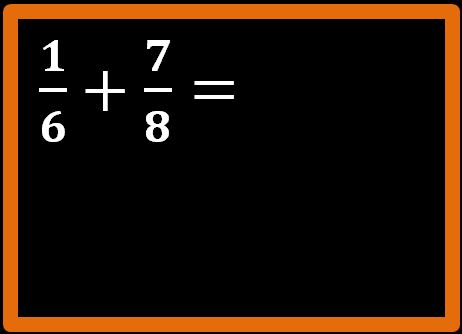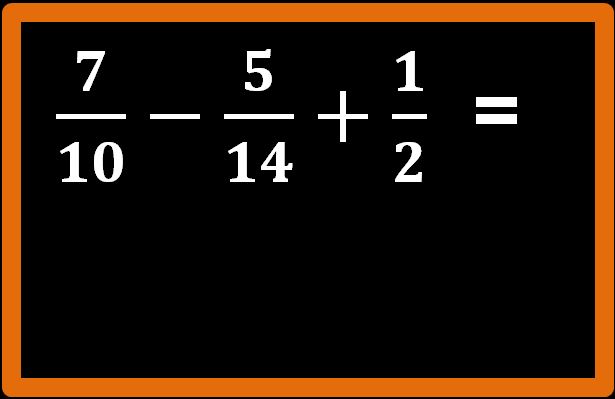Oggi la prof di matematica ha spiegato le frazioni e ha usato parole difficili come numeratore e denominatore. Alcuni tuoi compagni di classe già conoscevano le frazioni perché le avevano studiate alle elementari, ma tu non ne avevi mai sentito parlare. In classe non sei riuscito a capire né a cosa servono, né come si usano. Niente paura. Non ti preoccupare, con 5 minuti di impegno riuscirai a capire le frazioni e anche quelle parole difficili come numeratore e denominatore avranno un senso.
Dopo avere imparato cosa sono le frazioni e cosa significano, imparerai che esistono frazioni equivalenti e imparerai anche a effettuare addizioni e sottrazioni tra frazioni, a moltiplicare un numero per una frazione e poi tutte le altre operazioni. Ma facciamo un passo alla volta.
Indice
- Perché sono state inventate le frazioni?
- La tavoletta di cioccolato: esempio 1
- Quanto cioccolato è rimasto: esempio 2
- La pizza: esempio 3
- La torta: esempio 4
- Il rettangolo: esempio 5
- Esercizi
- Mettiti alla prova
Perché sono state inventate le frazioni?
Forse pensi che le frazioni siano sempre esistite. Invece non è così, le frazioni sono state inventate, come la ruota o il dentifricio. La prova più antica che abbiamo dell’uso delle frazioni risale all’ Antico Egitto. la storia è più o meno questa 😊.
Il Faraone si trovò di fronte a questo problema: aveva 5 pagnotte e doveva dividerle in parti uguali a 4 persone.
Ricorda:
Frazionare significa dividere in parti uguali.
In altre parole una frazione non è altro che una divisione scritta in un modo diverso.

Potrebbe sembrare una cosa divertente, invece era un procblema serio. La gente aveva fame. Tutti avevano diritto ad avere il pane nelle stesse quantità. Se il pane fosse stato diviso in modo sbagliato la popolazione poteva anche ribellarsi.
C’era poco da scherzare (in Francia qualche secolo dopo il popolo affamato avrebbe tagliato la testa al re e a molti dei suoi amici).
Non possiamo essere certi di come andò nella realtà, ma è molto probabile che il Faraone chiese a uno dei suoi scribi di risolvere il problema (lo scriba nell’Antico Egitto era una delle poche persone che sapeva scrivere, tutti i geroglifi che noi oggi vediamo sono stati scritti dagli scribi).
Lo scriba allora, dopo averci pensato un po’ su, divise ogni pagnotta in 4 parti uguali.
Per semplicità disegniamo le pagnotte rotonde. Quindi prima di aver diviso le pagnotte la situazione era questa:

Dopo aver diviso ciascuna pagnotta in 4 parti uguali, invece la situazione era questa:

Lo scriba sapeva sicuramente contare e sapeva effettuare una semplice divisione. Infatti si rese conto che dividendo le pagnotte in quel modo aveva ottenuto venti pezzi di pane della stessa grandezza.
Adesso non doveva fare altro che dare a ogni persona 5 pezzi di pane. In questo modo tutti avrebbero avuto la stessa quantità di pagnotta.
Il Papyrus Rhind
Lo scriba annotò tutto questo su un papiro che è arrivato fino a noi. Oggi puoi osservarlo al British Museum a Londra e si chiama Papyrus Rhind dal nome della persona che lo acquistò molto tempo fa. Quella che vedi sotto è la più antica testimonianza scritta dell’uso delle frazioni. Lo scriba aveva usato la frazione cinque quarti, vedremo più avanti cosa vuol dire.

Numeratore e denominatore
la tavoletta di cioccolato: esempio 1
Dopo questo breve viaggio nella storia della matematica, torniamo in classe e cominciamo a descrivere una frazione. Cominciamo subito con un esempio. A me piace molto il cioccolato. Supponiamo di avere una tavoletta di cioccolato.

Come puoi vedere la tavoletta è divisa in 8 quadretti uguali. Immaginiamo che io ne mangi solo 3. (Le parti che ho mangiato sono colorate di bianco).

Usando il linguaggio matematico si dice che ho mangiato 3 quadretti su 8. Se voglio usare una frazione, devo scrivere così:

Quindi per scrivere una frazione qualsiasi i passaggi sono 3:
- Per prima cosa si traccia una breve linea, che è chiamata linea di frazione.
- Sotto la linea va scritto il numero di parti uguali in cui è diviso l’intero (una tavoletta di cioccolato, una torta, una pizza, un numero, ecc.). Il numero che va sotto la linea di frazione è chiamato denominatore. Nel nostro esempio era 8.
- Sopra la linea di frazione si scrive il numero di parti che prendo in considerazione. Nel nostro esempio erano le parti che ho mangiato ed erano 3. Il numero che si trova sopra la linea di frazione si chiama numeratore.
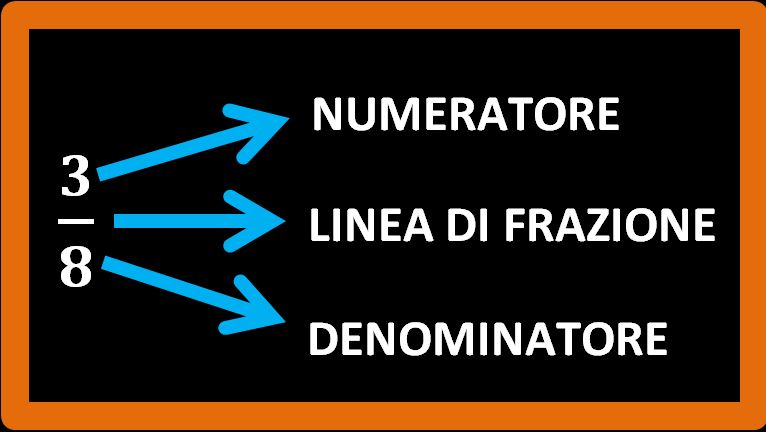
Chiaro? Forse sì e forse no. Facciamo ancora alcuni esempi per capire meglio.
Quanto cioccolato è rimasto: esempio 2
Ritorniamo alla mia tavoletta di cioccolato. Ti chiedo di scrivere sotto forma di frazione i quadretti rimasti, cioè quelli che non ho mangiato.

Procediamo passo passo. Come prima cosa scriviamo la linea di frazione:

Il secondo passaggio prevede di scrivere il denominatore. Cioè dobbiamo scrivere sotto la linea di frazione in quante parti uguali era divisa la tavoletta. Se guardi l’immagine vedi che i quadretti erano 8.
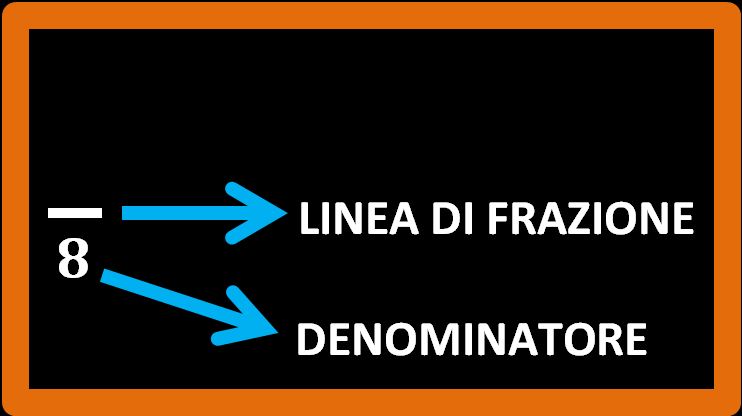
Adesso il terzo e ultimo passaggio. Dobbiamo scrivere il numeratore. Cioè dobbiamo scrivere le parti che prendiamo in considerazione. Nel nostro esempio dobbiamo considerare le parti che non ho mangiato, quelle che sono rimaste. Se andiamo a contare i quadretti rimasti vediamo che sono 5.
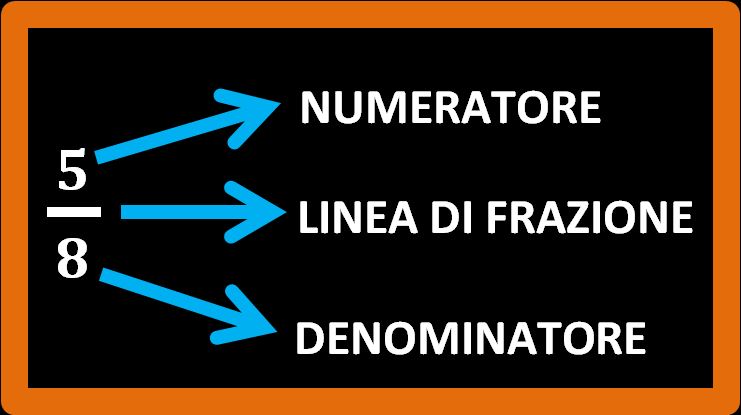
Fantastico. Tutto qua. Vediamo come si legge la frazione che abbiamo trovato.

(Non leggere 5 all’ottava perché è un errore. Cinque all’ottava è un elevamento a potenza con base 5 ed esponente 8 → 58 ).
La pizza: esempio 3
Per vedere se abbiamo capito cosa sono le frazioni: numeratore e denominatore, proviamo a scrivere ancora qualche altra frazione. Guarda la figura sotto.
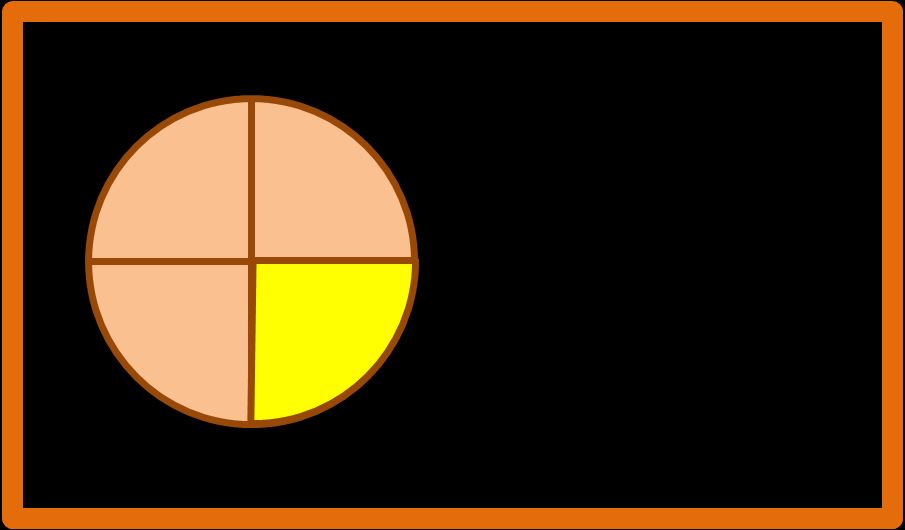
È un cerchio, se vuoi puoi immaginare che sia una torta o una pizza. Io scelgo la pizza.
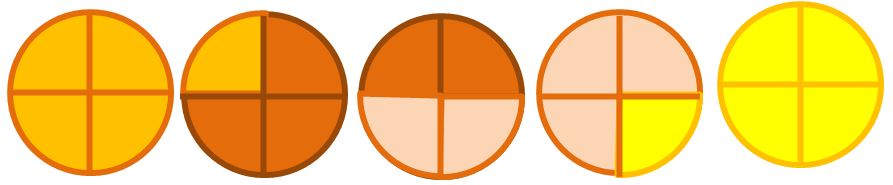
Bene, come vedi la nostra pizza è divisa in parti uguali. Dobbiamo scrivere sotto forma di frazione le parti colorate di giallo. La prima cosa che dobbiamo chiederci è :
- In quante parti uguali è divisa la pizza? La risposta è 4;
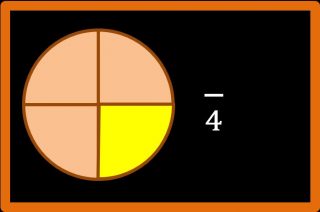
Poi dobbiamo chiederci:
- di queste 4 parti, quante ne devo considerare? A noi interessano solo le parti colorate in giallo, cioè 1.
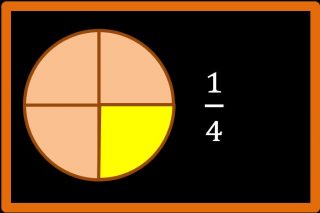
Quindi la frazione che cercavo è 1 su 4, che si può anche leggere un quarto.
1 è il numeratore. Invece 4 è il denominatore.
Esercizio concluso.
La torta: esempio 4
Facciamo un altro esempio per essere sicuri di avere capito le frazioni: numeratore e denominatore. Supponiamo di essere invitati ad un compleanno. Il festaggiato ha comprato una bella torta al cioccolato. La torta viene divisa nel modo che vedi nella figura sotto.

Gli invitati alla festa erano 7 e ognuno di loro mangia un pezzo di torta. Usando le frazioni, quale parte di torta è stata mangiata?
Per rispondere a questa domanda, la prima cosa da fare è contare in quante parti uguali è stata divisa la torta. Contandole attentamente vediamo che la torta è stata divisa in 8 parti. In altre parole l’intero è stato diviso in 8. Il numero 8 sarà il denominatore della frazione che stiamo cercando.
Il numeratore sarà dato dalle parti che prendiamo in considerazione, nel nostro esempio ci interessano le parti mangiate. Cioè 7.
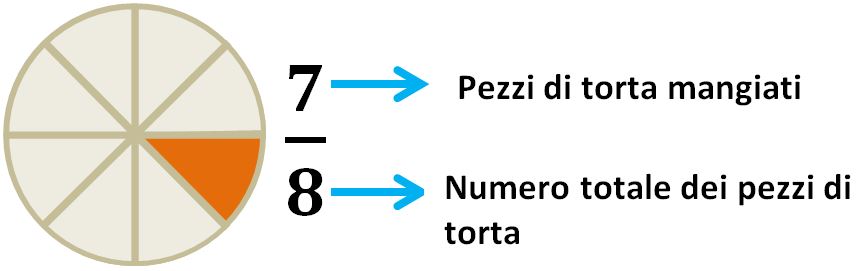
Sono stati mangiati i sette ottavi della torta. La frazione si può anche leggere 7 su 8 oppure 7 fratto 8. Guardando il disegno possiamo dire che è stata mangiata quasi tutta. Esercizio concluso.
Il rettangolo: esempio 5
Molto bene, ora che abbiamo preso un po’ di familiarità con numeratore e denominatore facciamo un esercizio veloce. Disegnamo un bel rettangolo e lo dividiamo in 6 parti uguali.
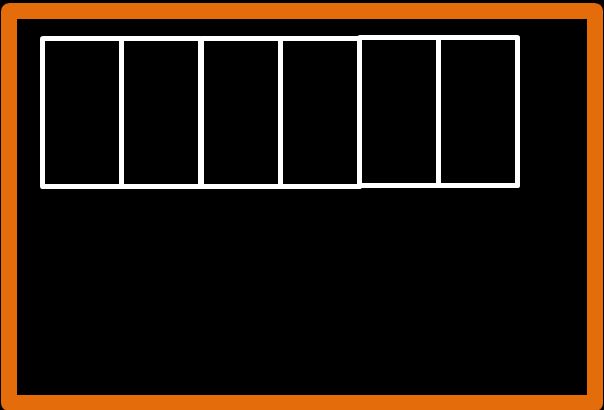
Se stai scrivendo su un foglio a quadri, ti puoi aiutare contando i quadretti. Disegna il rettangolo lungo 12 quadretti e poi traccia una tacca ogni due quadretti.
Ora colora i primi dua rettangoli, come nella figura che vedi sotto.

Benissimo. Ora dovresti essere in grado di scrivere sotto forma di frazione quale parte del rettangolo è stata colorata.
Le domande che dobbiamo porci sono:
- In quante parti uguali è diviso l’intero rettangolo?
- Quante parti ne considero (in questo caso: quante parti sono state colorate)?
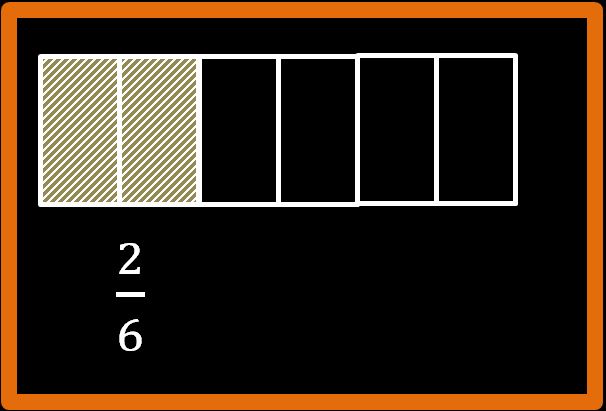
La risposta è due su sei oppure due sesti. Esercizio concluso.
E quale sarà la frazione che rappresenta la parte non colorata?
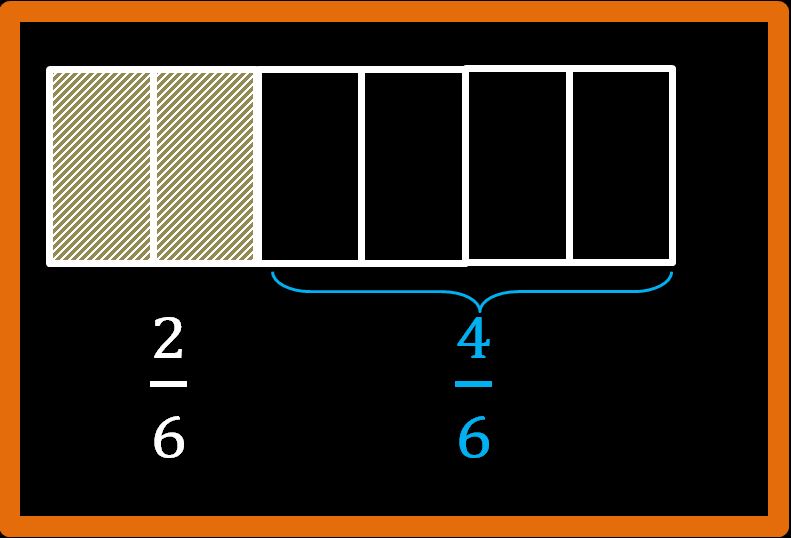
La risposta è 4 su 6, che si può leggere anche quattro sesti. Esercizio concluso.
Esercizi
Adesso possiedi gli strumenti per potere eseguire qualche esercizio che riguarda le frazioni, il numeratore e il denominatore. Se vuoi puoi metterti alla prova usando gli esercizi che trovi sotto. Puoi consultarli dal tuo pc o dal tuo smartphone o sulla LIM. Lavora con calma e non avere fretta di finire e leggi bene la consegna.


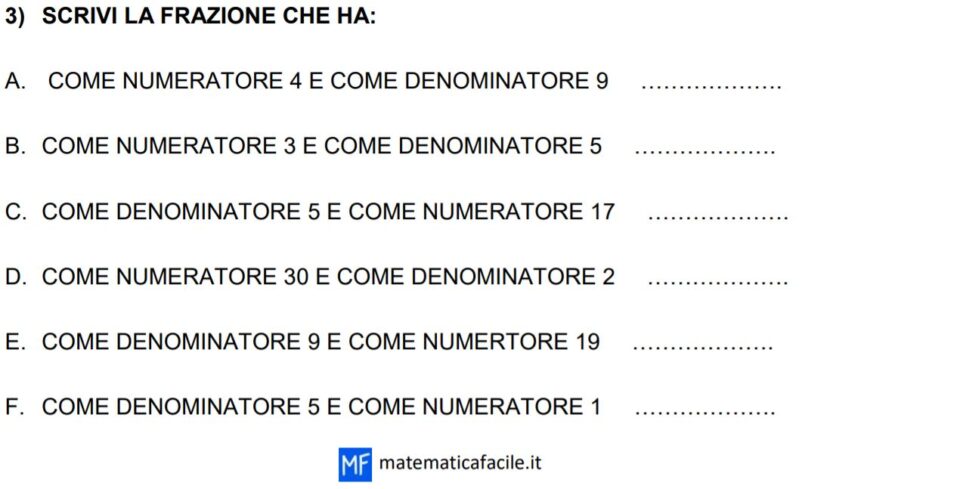
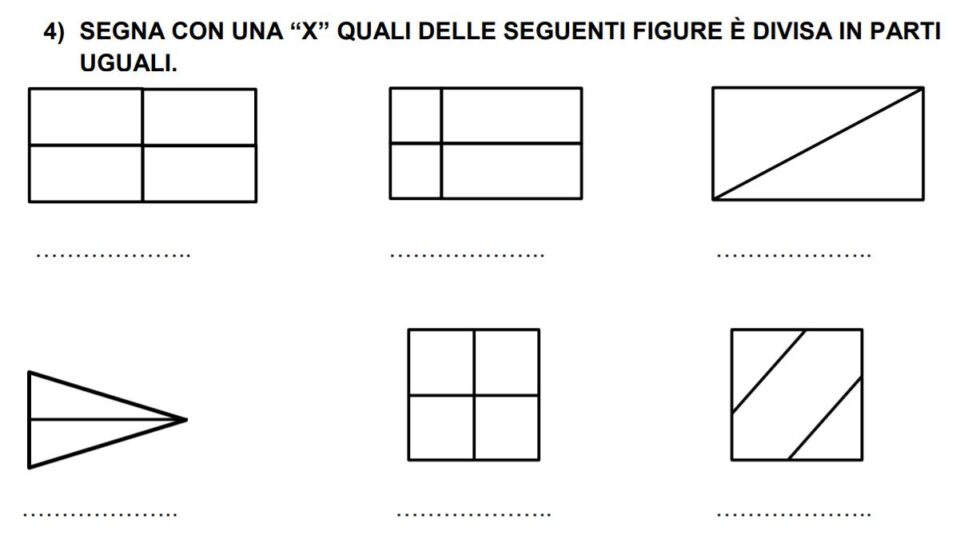
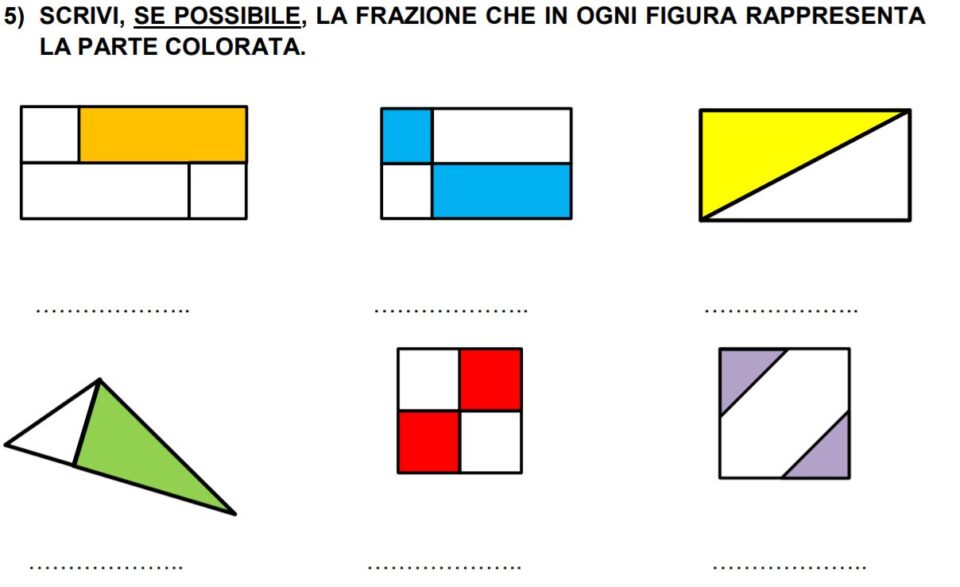

Buon lavoro.
Mettiti alla prova
Cliccando su questo link https://bit.ly/3OisDrY verrai indirizzato a un Modulo Google che ti permette di eseguire un breve test sulle frazioni.
Se vuoi consultare o scaricare le tavole numeriche puoi visitare questa pagina della Casa Editrice Zanichelli.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati a tutti quei lettori che segnaleranno eventuali errori presenti nell’articolo.