Non c’è niente da fare. Questo argomento di geometria analitica ti è risultato poco chiaro. Non ti preoccupare, capita a tutti di non capire qualche argomento. Con 5 minuti di impegno riuscirai a calcolare la lunghezza di qualsiasi segmento inclinato rispetto agli assi cartesiani.
Indice
Esempio 1
Cominciamo subito con un esempio numerico. Tracciamo su un piano cartesiano i punti
A(1; 3) e B(11; 5)
Ricordiamoci che la prima coordinata è l’ascissa e indica di quanto ci spostiamo sull’asse X, invece la seconda coordinata si chiama ordinata e ci indica di quanto ci spostiamo sull’asse Y.
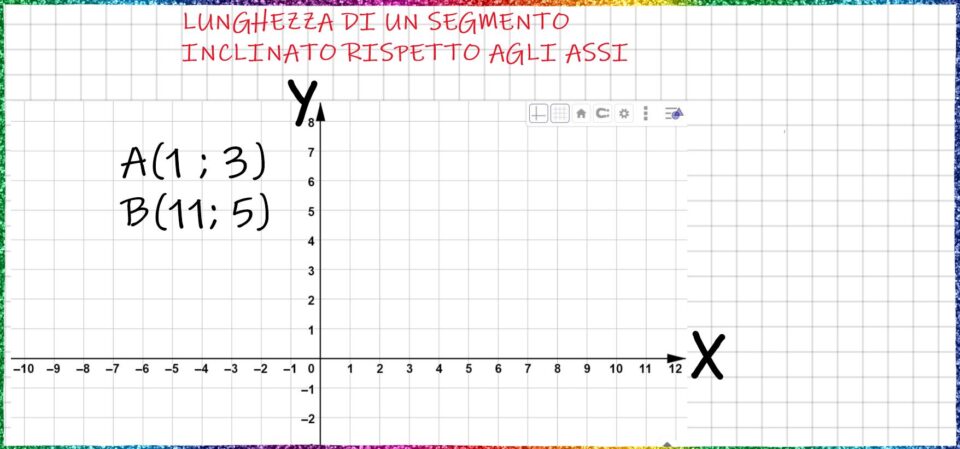
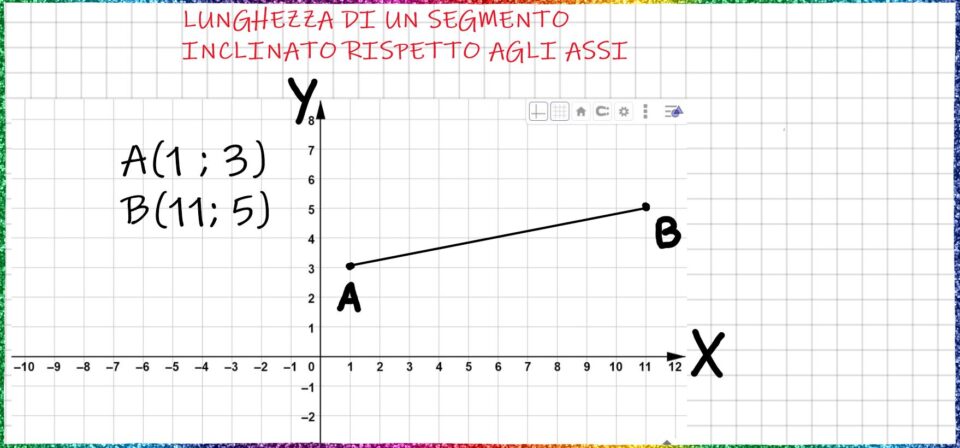
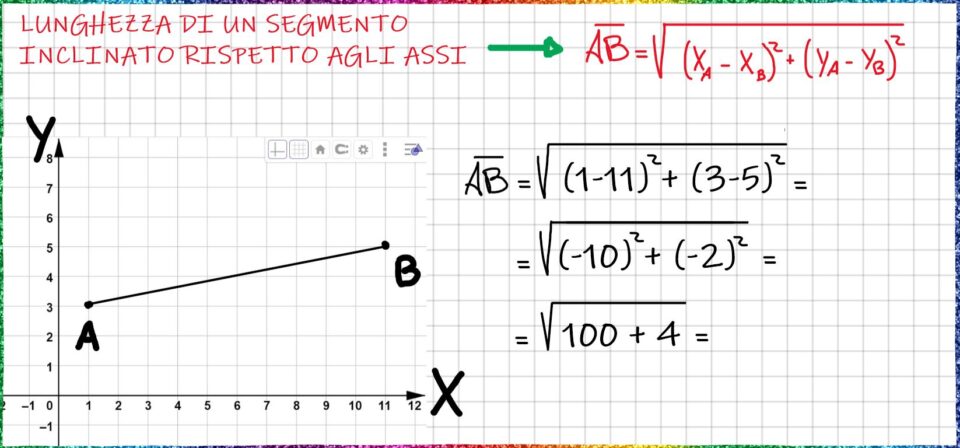
Dopo avere tracciato i punti li uniamo ottenendo il segmento AB, come vedi nell’immagine in basso.
Il nostro scopo è calcolare la lunghezza del segmento, oppure se vogliamo dirla in modo diverso, dobbiamo calcolare la distanza tra il punto A e il punto B.
La formula che devi usare, la trovi in basso. È l’applicazione del Teorema di Pitagora nella geometria analitica usando le coordinate dei punti.

Passiamo all’applicazione della formula. Mettiamo al posto dei simboli i numeri. Per esempio:
invece di XA scriviamo 1 e invece di XB scriviamo 11. Questo perchè:
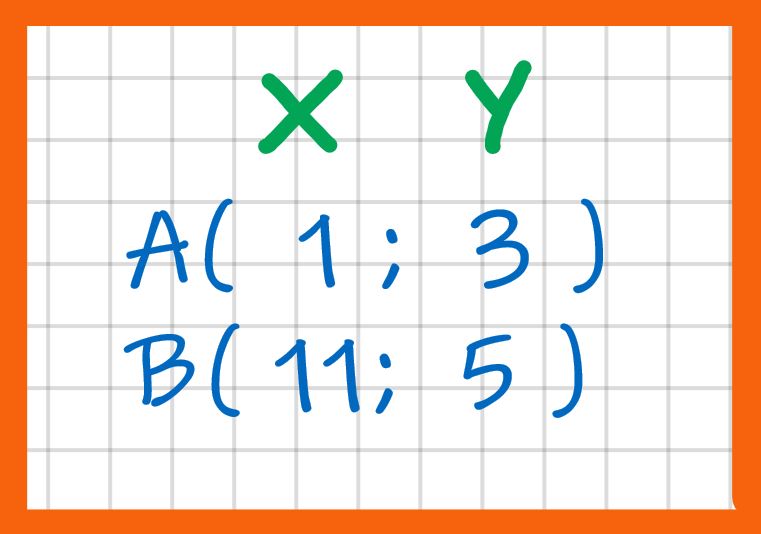
Dopo avere sostituito anche le Y, otteniamo l’espressione che leggi nell’immagine in basso.

Ora dobbiamo risolvere un’espressione con le radici. Se non ti ricordi come si fa, potresti dare un’occhiata al mio articolo le espressioni con le radici quadrate.
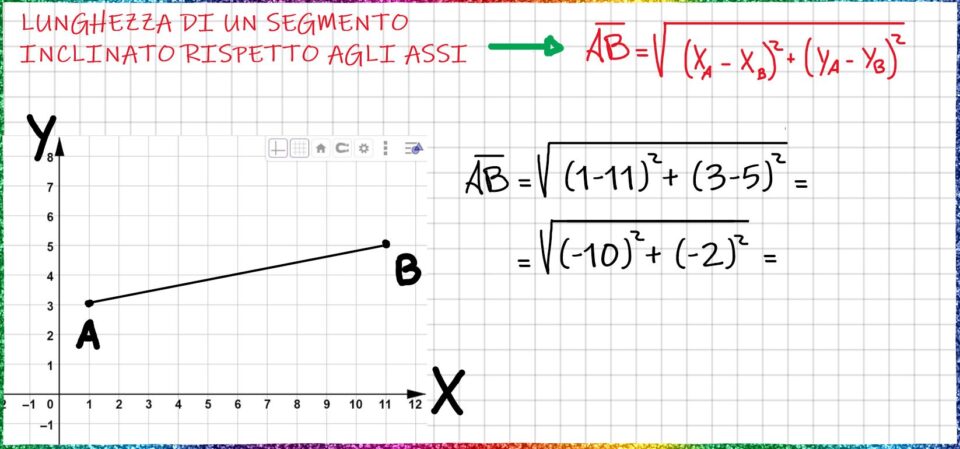
La prima cosa da fare sono i calcoli all’interno delle parentesi tonde. Nella prima tonda dobbiamo eseguire la sottrazione:
1-11 = -10
È una sottrazione che ha come risultato un numero negativo. Se vuoi ripassare le operazioni con i numeri relativi (quelli che hanno il segno meno davanti) potresti dare un’occhiata al mio articolo come si esegue la sottrazione tra numeri relativi.
Dobbiamo poi elevare alla seconda -10. Cioè bisogna eseguire una potenza con base negativa. Come vedi gli argomenti da sapere sono tanti, ma in matematica funziona così. Ogni argomento è utile per potere capire i concetti successivi.
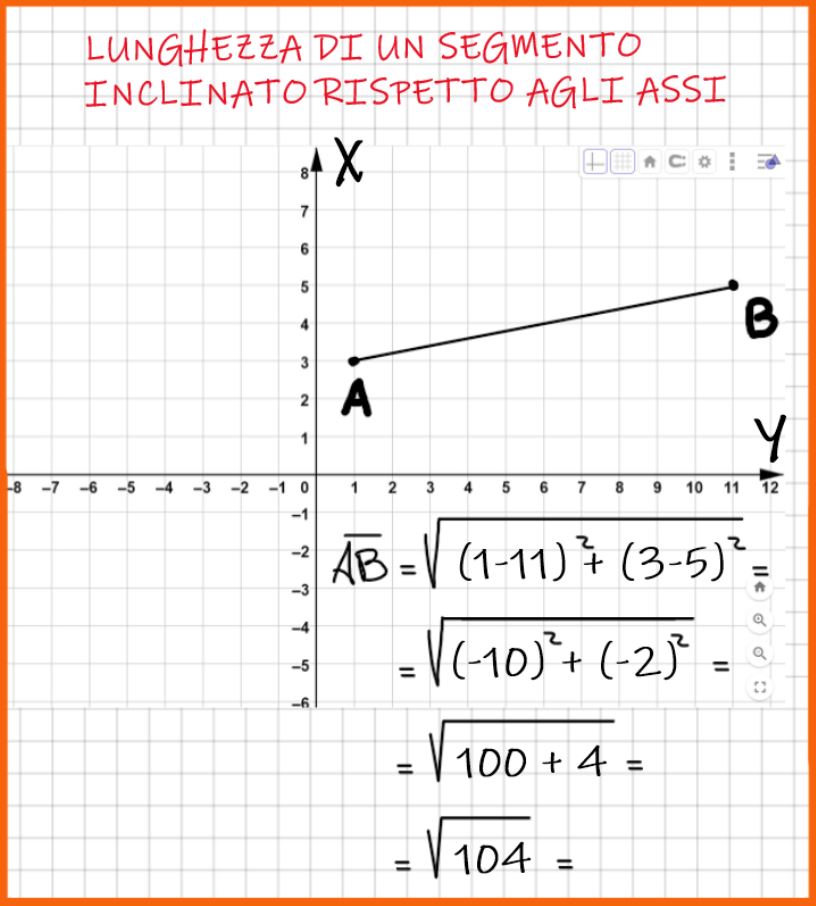
Per determinare la radice quadrata di 104 puoi usare le tavole numeriche oppure puoi usare la calcolatrice. Questo dipende dalla tua prof.
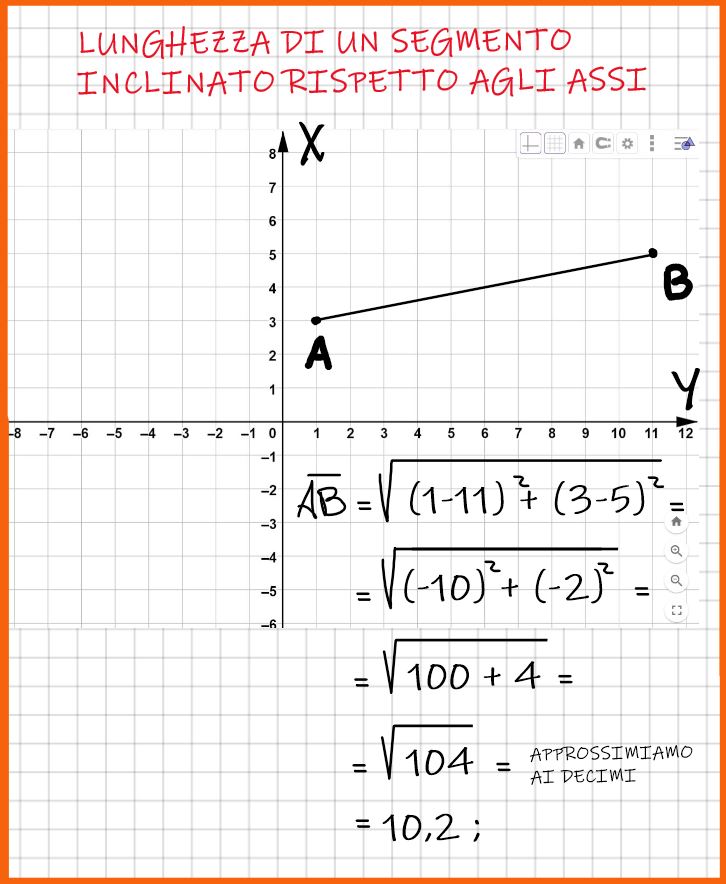
Approssimiamo (si può anche dire arrotondiamo) ai decimi, cioè alla prima cifra decimale e otteniamo come risultato 10,2. Se non ti ricordi come si approssimano i numeri, potresti leggere il mio articolo, come si approssimano i numeri decimali.
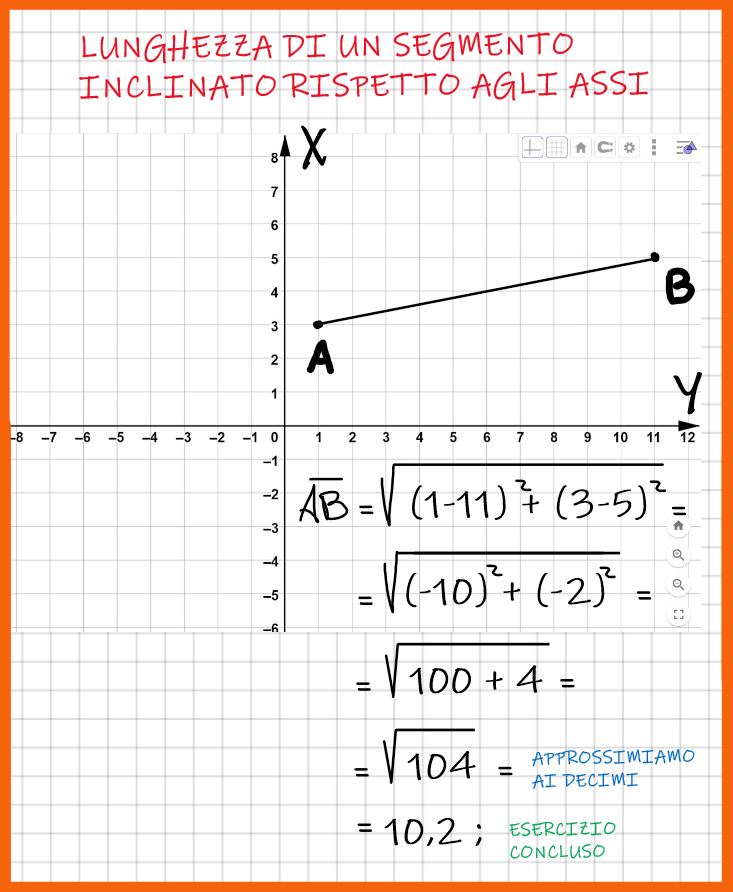
Esercizio concluso.
Esempio 2
Vediamo un altro esempio svolto per cercare di capire come si calcola la lunghezza di un segmento inclinato rispetto agli assi. In questo secondo esempio i punti hanno coordinate:
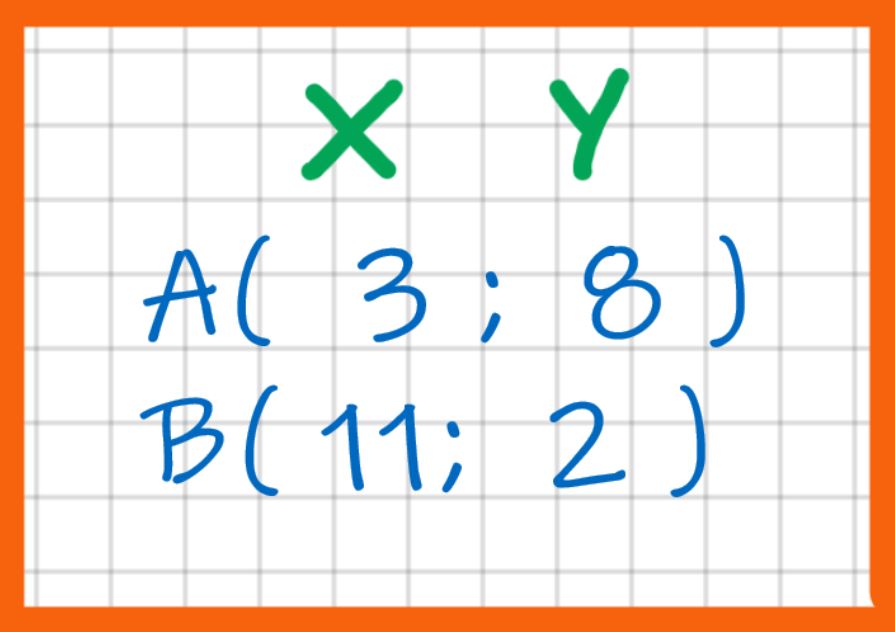
Andiamo veloci. Applichiamo la formula:

E sostituendo i simboli con i numeri otteniamo:
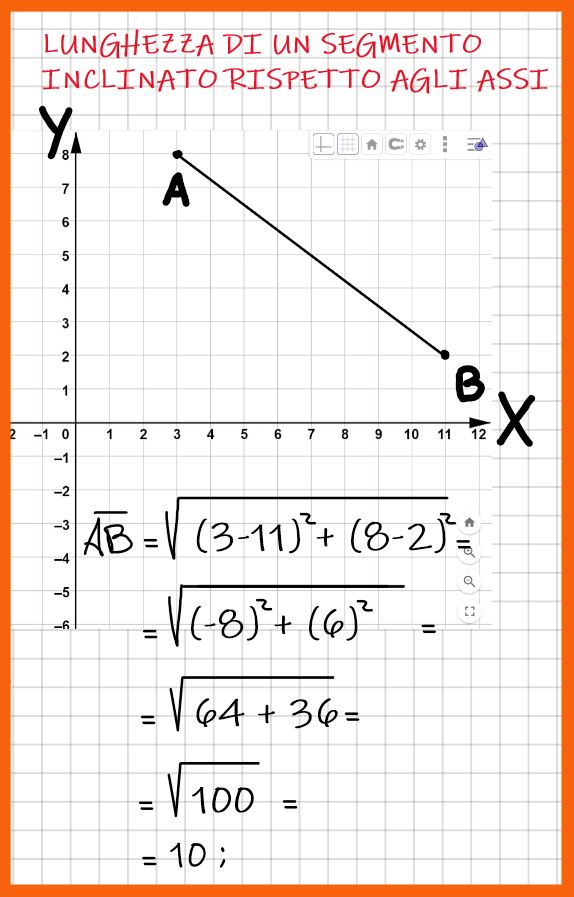
Esercizio concluso.
Terzo esempio
Ecco un altro esempio svolto. In questo caso i punti cadono nel secondo e nel terzo quadrante.
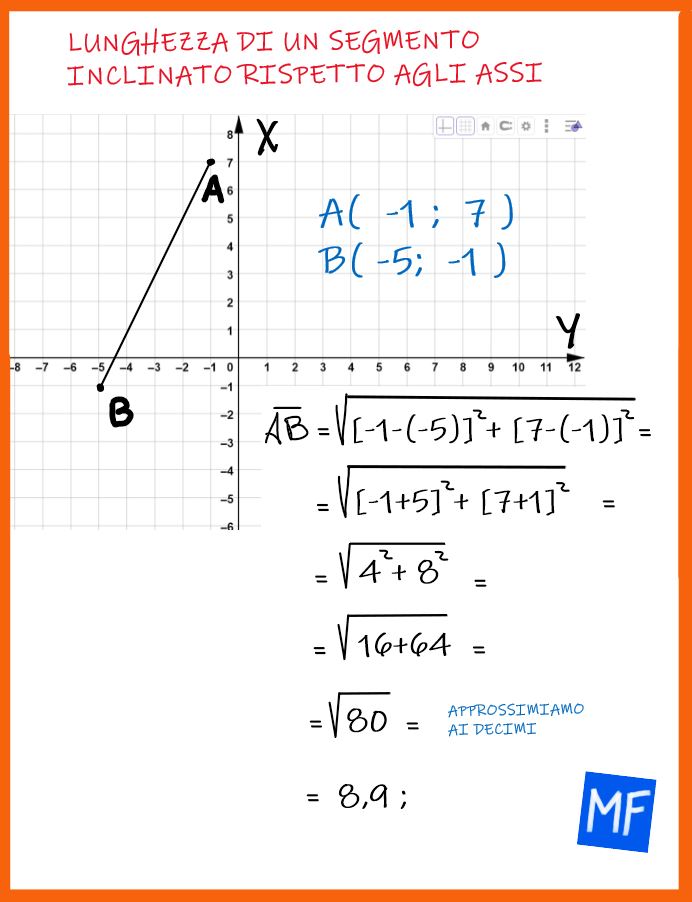
Primo esercizio
Se vuoi puoi metterti alla prova con l’esercizio che trovi in basso. Lavora con calma e non ti preoccupare se sbagli. Se aguzzi la vista, trovi anche il risultato che ti serve per capire se hai lavorato bene oppure no.
- Determina per prima cosa le coordinate dei punti;
- Calcola la lunghezza del segmento AB, approssimando se necessario ai decimi.
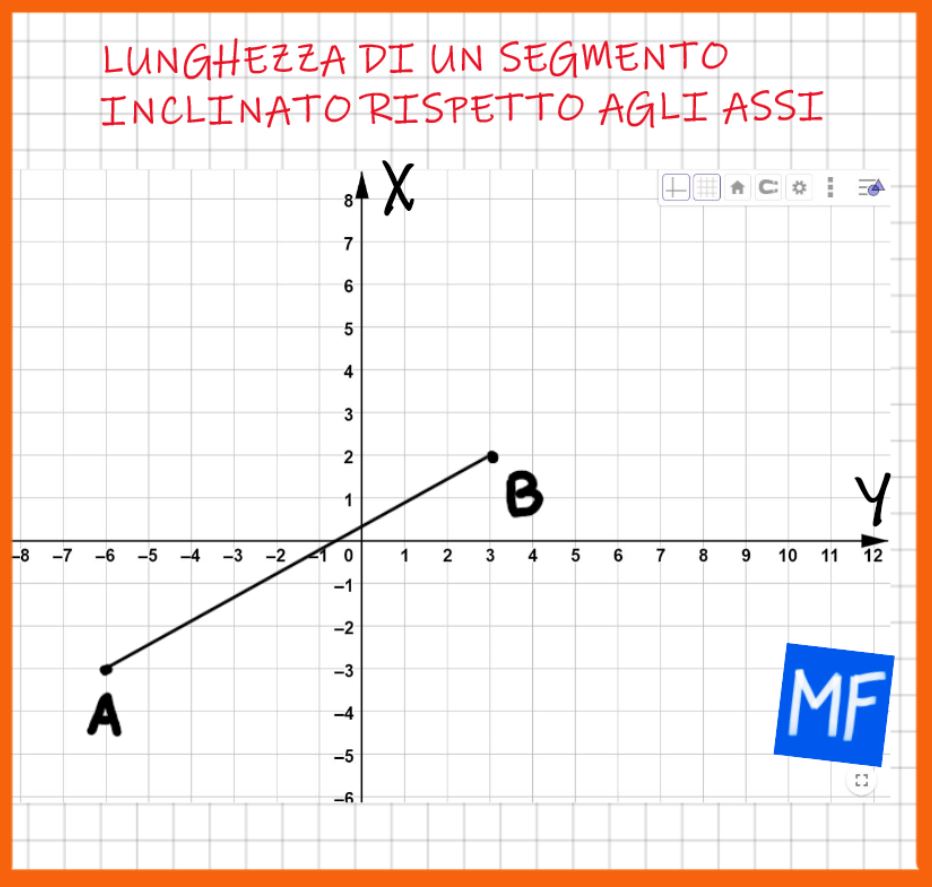
Il risultato è 10,3
Secondo esercizio
- Determina le coordinate dei punti A e B.
- In quali quadranti cadono i due punti?
- Qual è la lunghezza del segmento AB? Approssima se necessario il risultato ai decimi.
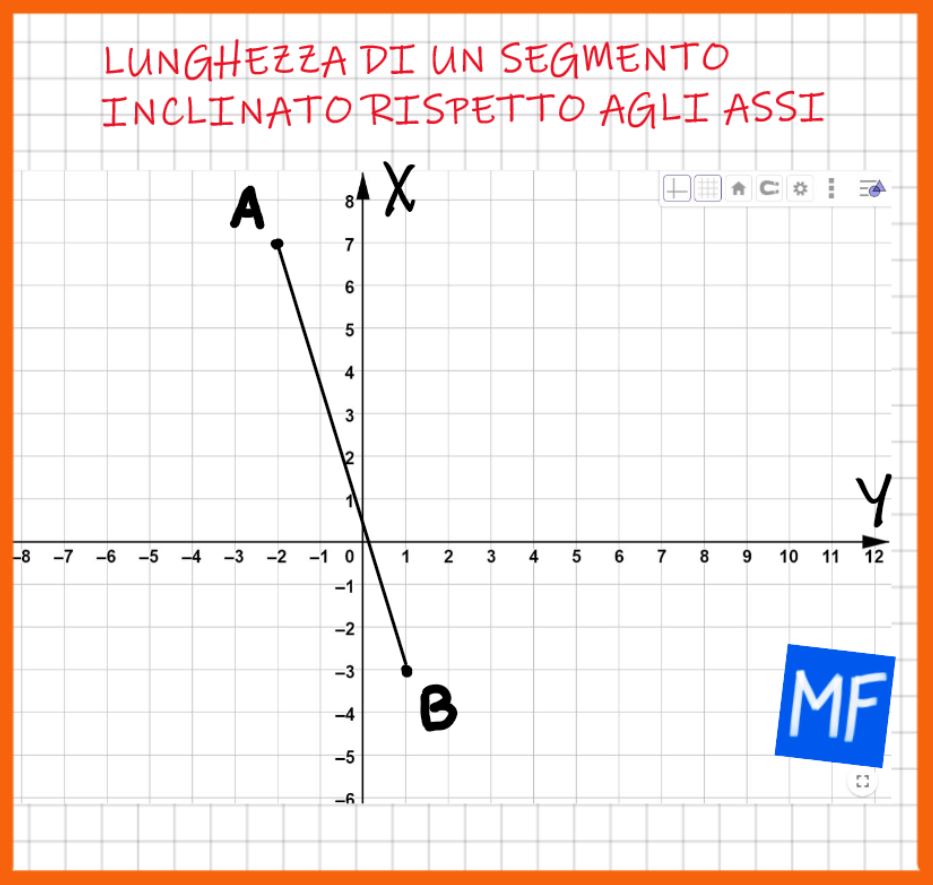
Buon lavoro. A(-2;7) B(1;-3). Secondo e quarto quadrante. AB = 10,4
Le immagini di questo articolo sono state create usando il software free Whiteboard, la cui pagina ufficiale è raggiungibile a questo link.
Se hai domande o vuoi segnalare un errore puoi contattarci attraverso le nostre pagine social oppuer puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori.