Molto bene, hai imparato a calcolare il minimo comune multiplo, ma ancora non riesci a capire a cosa serve. Non vedi quale sia la sua utilità. Leggendo questo articolo ti renderai conto che saper calcolare il minimo comune multiplo è essenziale per eseguire la somma tra frazioni con denominatore diverso. E poi forse ti tornerà utile anche nel Test INVALSI, motivo per cui vale la pena impiegare cinque minuti del tuo tempo.
In questo articolo cercheremo di capire come si esegue la somma tra due frazioni che hanno denimonatore diverso. Per semplicità iniziamo considerando solo due frazoni, ma il procedimento che seguiremo è valido anche se avessimo a che fare con 3 o più frazioni. Non dobbiamo però avere premura. Iniziamo con le cose semplici. Impariamo prima a camminare e poi ci metteremo a correre.
Se invece vuoi sapere come si eseguono addizione e sottrazione tra frazioni che hanno lo stesso denominatore ti consiglio di dare un’ occhiata al mio articolo.
Indice
Addizione tra due frazioni con denominatore diverso
Esempio 1
La cosa migliore da fare è partire subito con un esempio numerico.
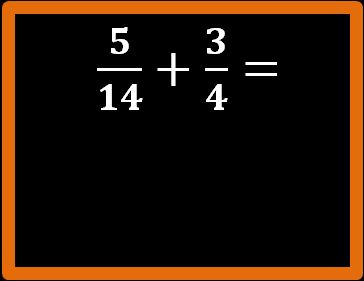
Per risolvere questa addizione si procede in questo modo. Il primo passaggio da eseguire è trovare il minimo comune multiplo tra i denominatori. Ti ricordo che in una frazione il denominatore è tutto ciò che si trova sotto la linea di frazione. Nel nostro esempio i denominatori sono i numeri 14 e 4.
passaggio 1: trovare l’ m.c.m. tra i denominatori
Per trovare l’m.c.m. tra due numeri è necessario scomporli in fattori primi. Poi scegliere i fattori comuni e non comuni presi una sola volta con l’esponente maggiore.
Se non ti ricordi come calcolare l’m.c.m. è il caso di andarlo a ripassare, altrimenti non possiamo andare avanti. Voler sommare frazioni con denominatore diverso è come voler costruire il primo piano di una casa in cui il piano terra è formato dal minimo comune multiplo.
Una volta chiarito questo, possiamo andare avanti con il nostro esempio e calcoliamo la somma tra frazioni con denominatore diverso. Cerchiamo di trovare il minimo comune multiplo tra i denominatori.

Continuiamo, ricordati che bisogna scomporre in fattori primi. Se non ti ricordi come si fa o vuoi rapassare un po’ prima di continuare, puoi dare un’ occhiata a questo mio articolo.

Possiamo adesso calcolare l’m.c.m..

Passaggio 2: usiamo l’m.c.m.
E adesso? Cosa me ne faccio del minimo comune multiplo? Vediamolo subito.
Ricordiamoci che il nostro scopo era sommare le frazioni cinque quattordicesimi e tre quarti.
Tracciamo una linea di frazione un po’ più lunga del solito e scriviamo come denominatore il minimo comune multiplo, cioè 28.
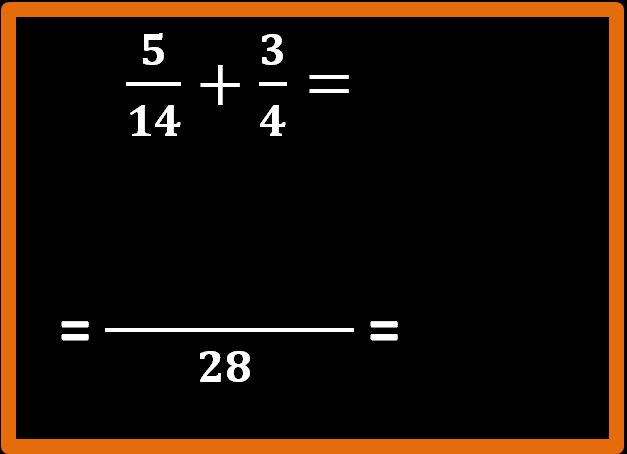
Determiniamo il numeratore
Ora attenzione, per determinare cosa scrivere al numeratore si procede così.
Dobbiamo dividere l’m.c.m. per il denominatore della prima frazione e poi moltiplicare il risultato per il numeratore.
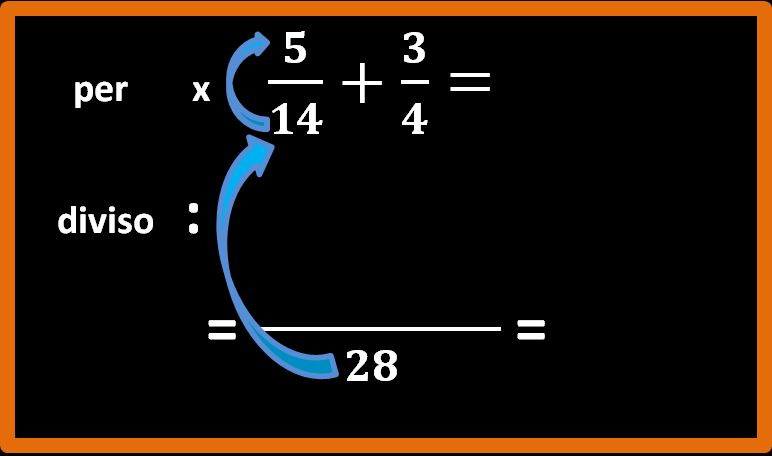
È più facile farlo che spiegarlo. Facciamo i conti con i numeri.
28 : 14 = 2; 2 · 5 = 10;
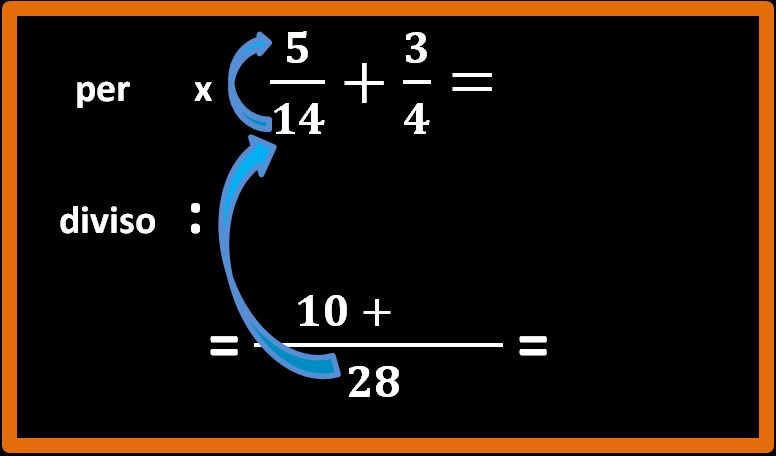
Riscriviamo il segno ” + ” dell’addizione e ripetiamo lo stesso procedimento per la seconda parte dell’addizione.
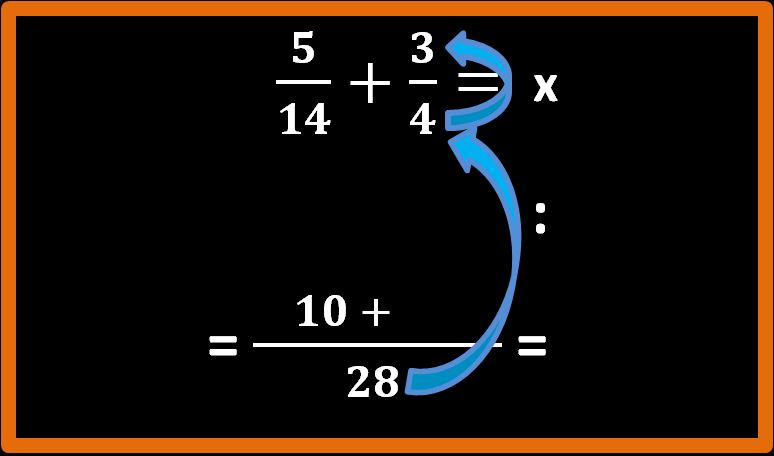
28 : 4 = 7; 7 · 3 = 21;
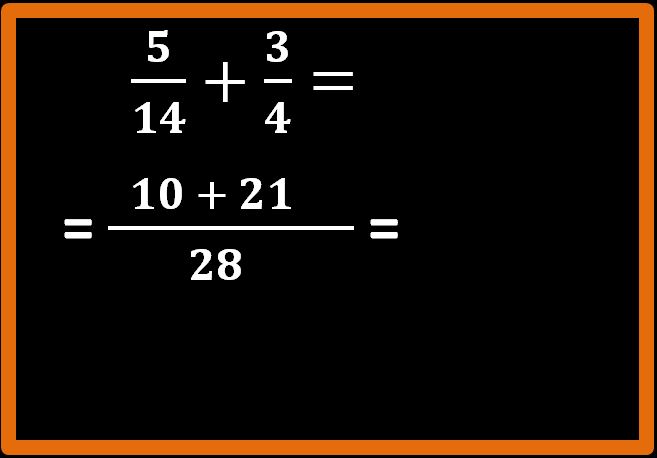
Non ci rimane che eseguire la somma al numeratore: 10 + 21 = 31
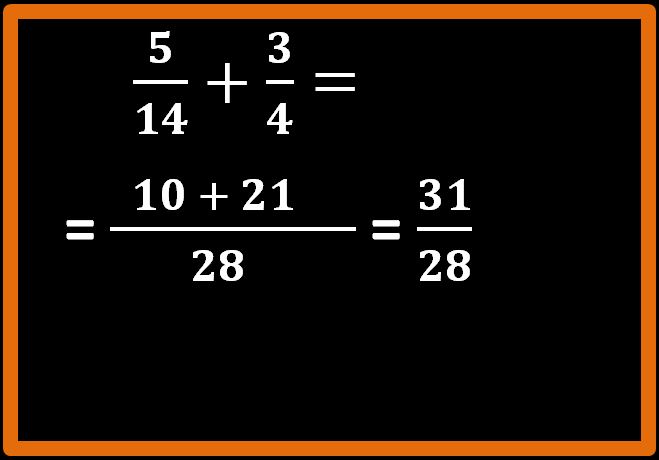
Abbiamo concluso.
Il risultato dell’addizione di cinque quattordicesimi più tre quarti è trentuno ventottesimi, che si può leggere anche 31 su 28 oppure 31 fratto 28.
Esempio 2
Continuiamo con un altro esempio. Credo che uno dei modi migliori per capire un argomento come questo sia fare degli esempi con i numeri.
Eseguiamo la somma un sesto più sette ottavi.
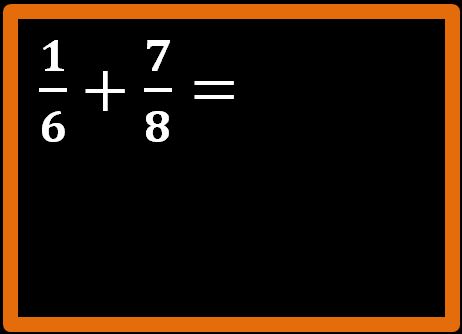
Passaggio 1
La prima cosa da fare è daterminare l’ m.c.m. tra i denominatori, che in questa addizione sono 6 e 8.
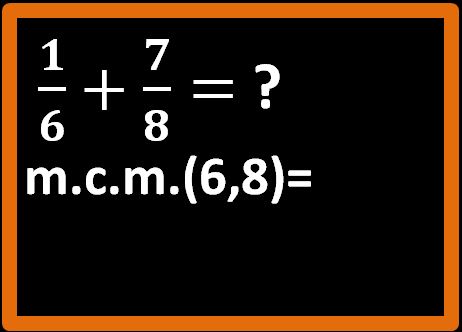
Ti ricordo che per calcolare l’m.c.m. dobbiamo scomporre i numeri in fattori primi e poi scegliere i fattori comuni e non comuni presi una sola volta con il maggiore esponente. Se la regola non ti è chiara, è possibile ripassarla leggendo questo mio articolo in cui viene spiegato come calcolare l’ m.c.m..
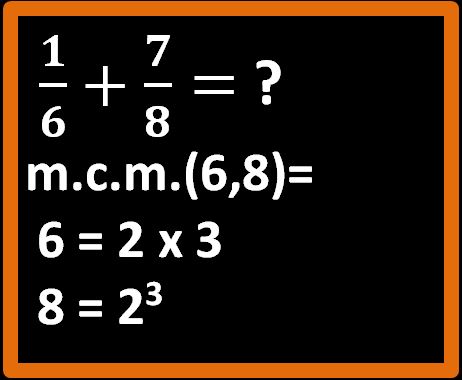
Dopo avere scomposto in fattori primi, andiamo a scegliere i fattori che ci permettono di calcolare l’m.c.m. e li cerchiamo di blu per essere sicuri di fare bene.
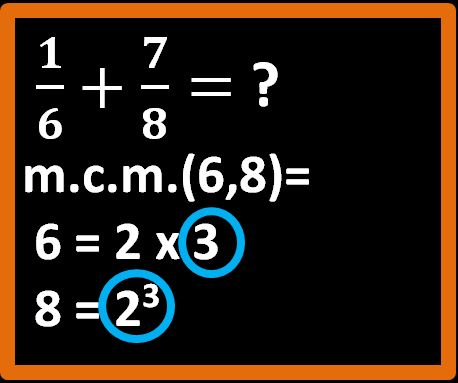
Molto bene, quindi per trovare l’m.c.m. dobbiamo moltiplicare:
23 · 3 = 8 · 3 = 24
Il numero 24 è il nostro minimo comune multiplo.
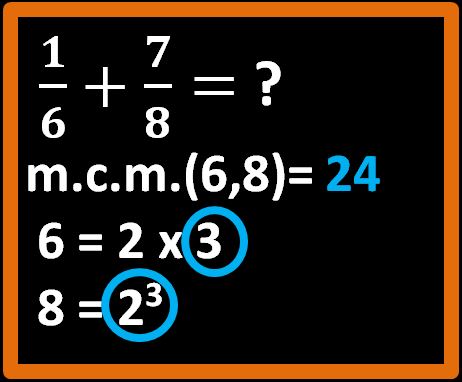
Passaggio 2
Adesso tracciamo una bella linea di frazione e mettiamo il 24 al denominatore della nostra frazione:
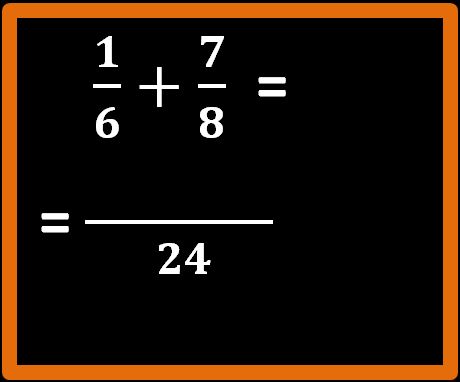
Ora dobbiamo fare queste operazioni: m.c.m. diviso denominatore della prima frazione e il risultato per il numeratore.
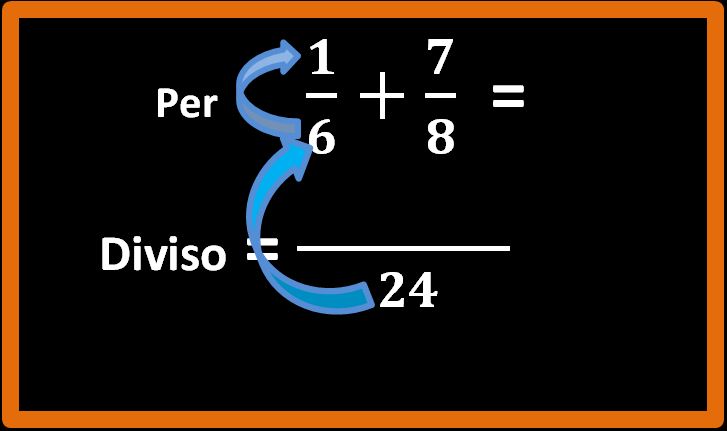
m.c.m. : denominatore = 4; 4 · numeratore = 4
24 : 6 = 4; 4 · 1 = 4
Il primo elemento che andremo a scrivere al numeratore è quindi 4. Si riscrive il segno ” + ” dell’addizione.
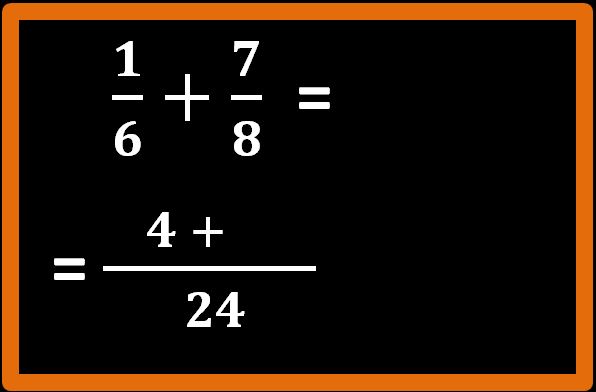
Si deve adesso ripetere lo stesso procedimento per la seconda frazione.

Le operazioni che dobbiamo svolgere sono:
24 : 8 = 3; 3 · 7 = 21;
il 21 è il secondo addendo dell’addizione presente al numeratore.
(Possono sembrare parole difficili, ma bisogna abituarsi a usare un linguaggio tecnico. Vedrai che la tua prof apprezzerà.)
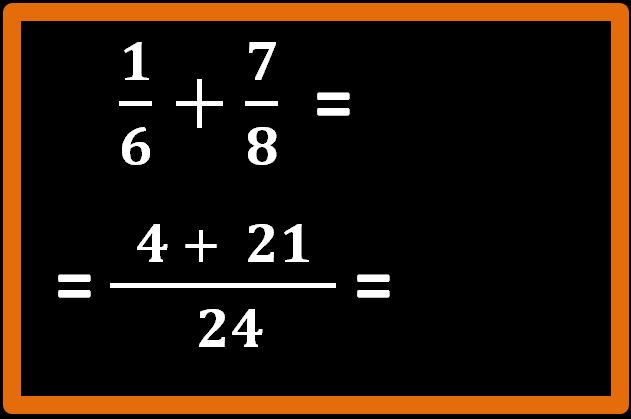
Non ci rimane che eseguire la addizione presente al numeratore, cioè 4 + 21.
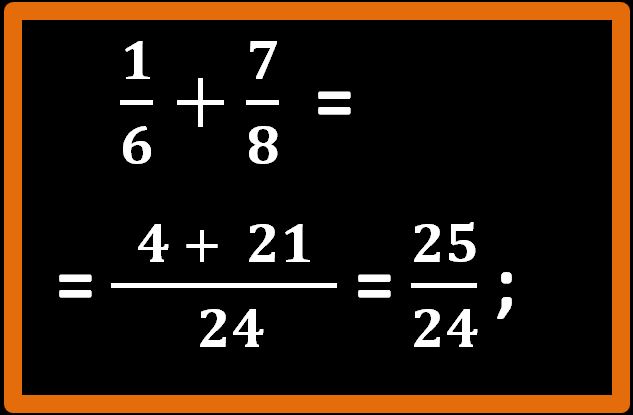
Il risultato che stavamo cercando è venticinque ventiquattresimi oppure detto in modo più semplice 25 su 24. Abbiamo finito.
Vedrai che con l’esercizio i passaggi diventeranno via via sempre più veloci. Ma sono necessari molti esercizi. Nessuno diventa brava/o in una settimana. Quindi non arrenderti e continua a impegnarti.
Sottrazione tra due frazioni con denominatore diverso
Per quanto riguarda le sottrazioni, il procedimento da seguire è identico a quello usato per la somma tra frazioni con denominatore diverso. Niente di nuovo. L’unica differenza è che le frazioni vanno sottratte e non addizionate. Ma passiamo subito a un esempio numerico.
Esempio 3
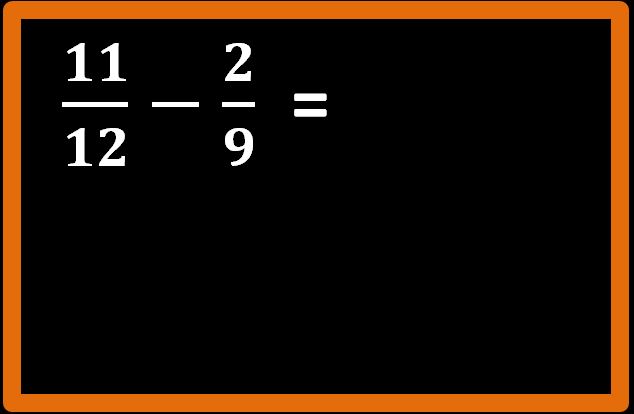
Come sempre il primo passaggio da fare è quello di trovare il minimo comune multiplo tra i denominatori.
Quindi dobbiamo scomporre in fattori primi il 12 e il 9. (Se vuoi vedere o scaricare le Tavole Numeriche, la casa editrice Zanichelli a questo link mette a disposizione un file pdf che contiene le tavole; le puoi visionare o scaricare sul tuo pc per averle a disposizione quando vuoi senza bisogno di collegarti ogni volta al sito.)
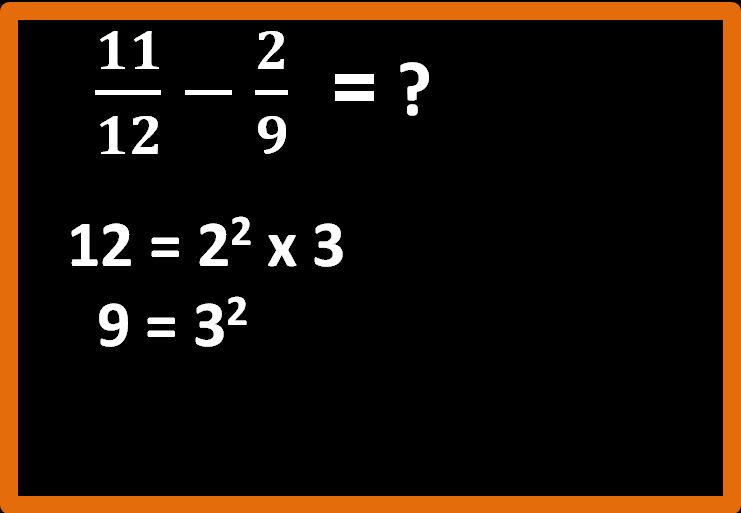
Dopo avere fatto ciò, calcoliamo l’m.c.m..
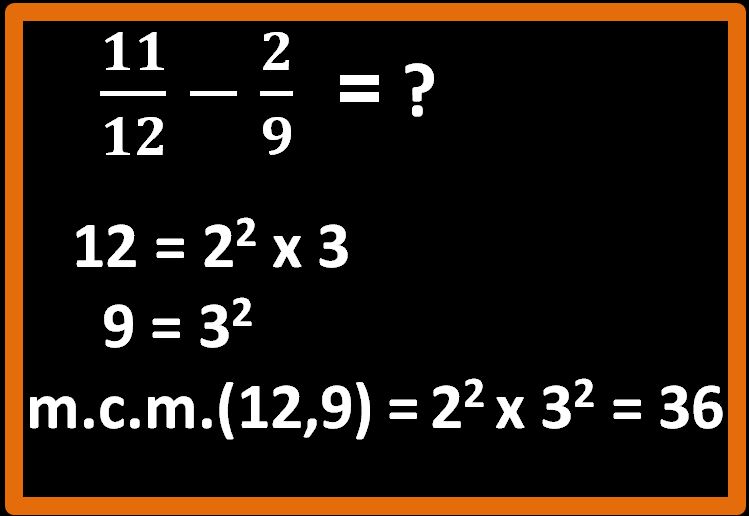
Bene, il nostro m.c.m. è 36. Ora tracciamo una bella linea di frazione e mettiamo il 36 come denominatore.
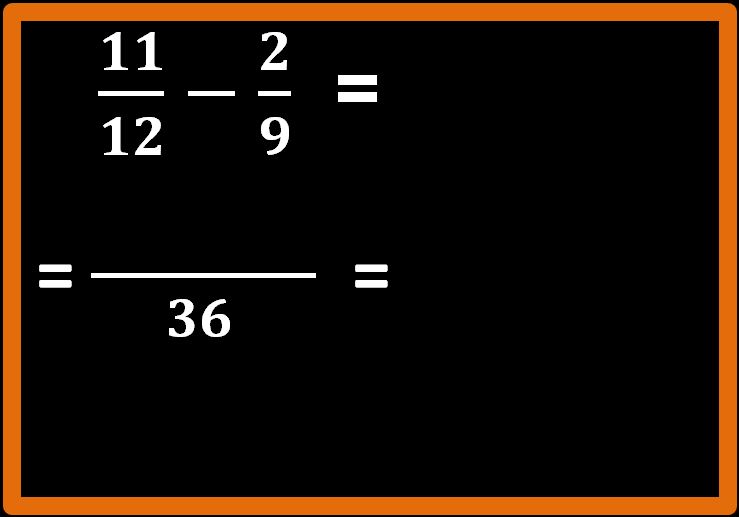
Il procedimento è identico a quello visto per le addizioni, cioè le operazioni che dobbiamo eseguire sono:
36 : 12 = 3; 3 · 11 = 33
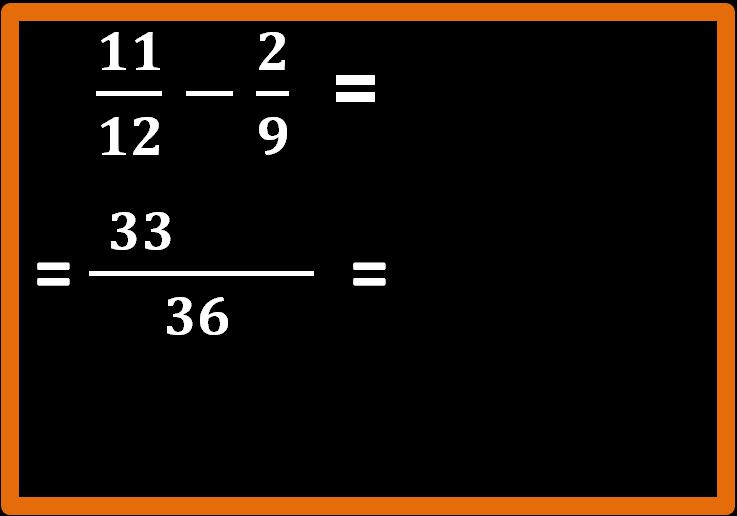
Attenzione adesso. Non dobbiamo scrivere “più”, ma “meno” perchè abbiamo a che fare con una differenza. Può sembrare una cosa banale da dire, ma molti errori nelle verifiche sono proprio di questo tipo. Errori dettati dalla fretta e/o dalla distrazione. Per cui calma e occhi aperti.
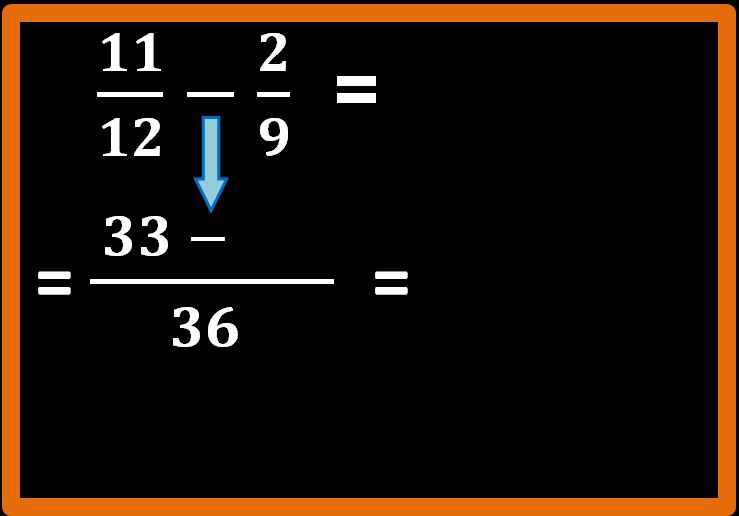
Il sottraendo della nostra differenza è dato da:
36 : 9 = 4; 4 · 2 = 8;
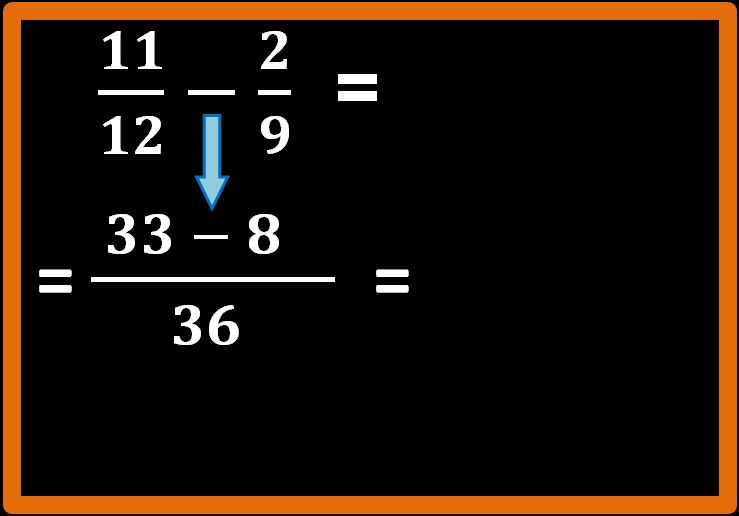
Non ci rimane che eseguire la differenza che compare al numeratore, cioè 33 – 8 = 25.
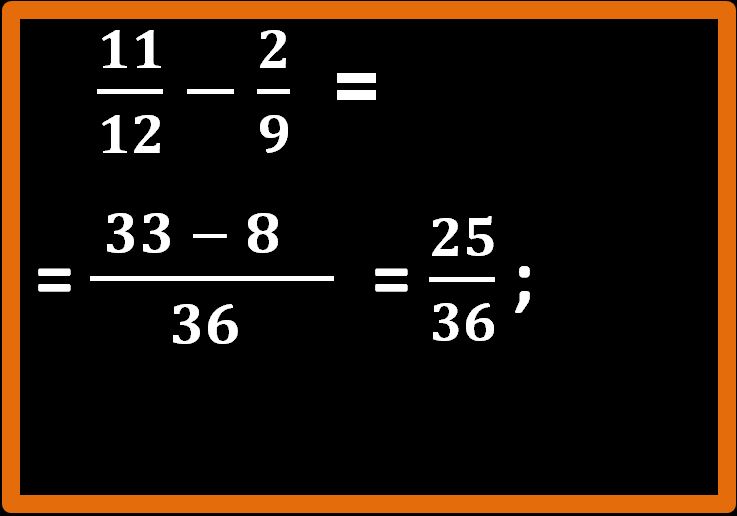
Il risultato che stavamo cercando è 25 su 36 che si può leggere anche venticinque trentaseiesimi. Come vedi per la somma tra frazioni con denominatore diverso si segue lo stesso procedimento della differenza, bisogna solo fare attenzione ai segni.
Esercizi
Adesso se vuoi, puoi provare da sola. Hai tutti gli strumenti per farcela. Se vuoi puoi esercitarti con gli esercizi che trovi sotto. Lavora senza fretta e non avere paura di sbagliare. Sbagliando si impara.

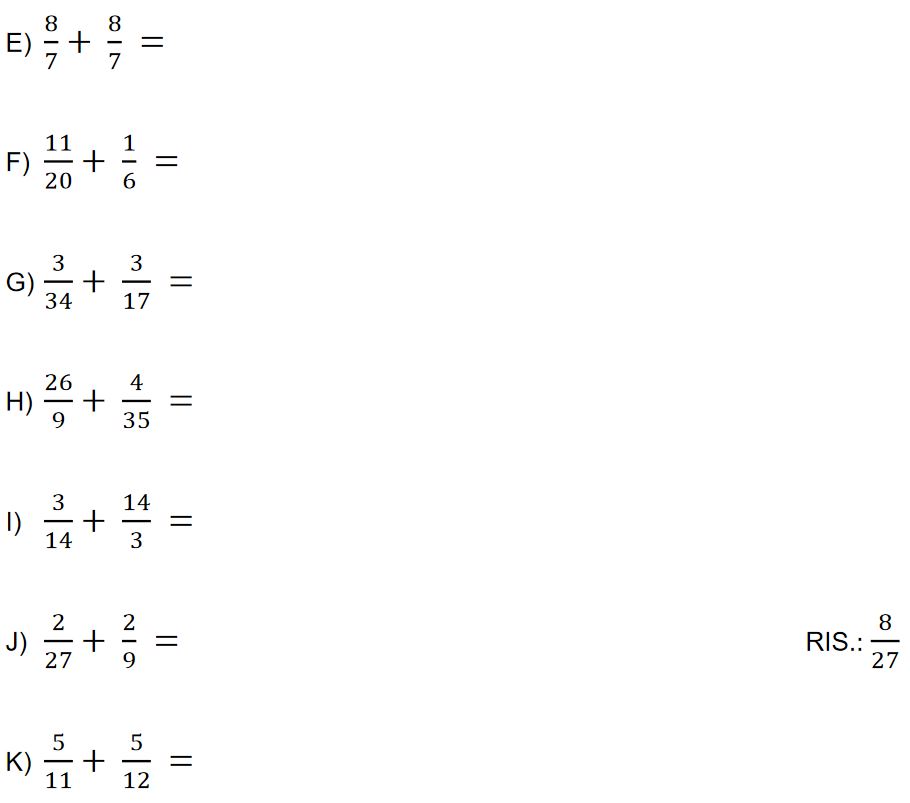
Buon lavoro.
Se hai dubbi o vuoi porre qualche domanda, puoi scrivere alla casella mail: matematica.facile@libero.it