Oggi in classe la tua prof ha spiegato la somma tra frazioni con lo stesso denominatore, ma tu non eri proprio attento attento e ti sei perso qualche passaggio. Poi quando a casa hai provato a fare gli esercizi ed ecco che non ti riescono. Non ti preoccupare, con cinque minuti di impegno saprai eseguire la somma tra due o più frazioni con lo stesso denominatore.
Indice
- Un breve ripasso
- Esempio 1
- Esempio 2
- Esempio 3
- Esempio 4
- Esempio 5
- Esempio 6
- Esempio 7
- Esempio 8
- Esempio 9
- Esercizi
Un breve ripasso
Ti ricordo che una frazione si compone di tre elementi:
- una linea di frazione;
- il numeratore (tutto quello che sta sopra la linea di frazione);
- il denominatore (tutto quello che sta sotto la linea di frazione).
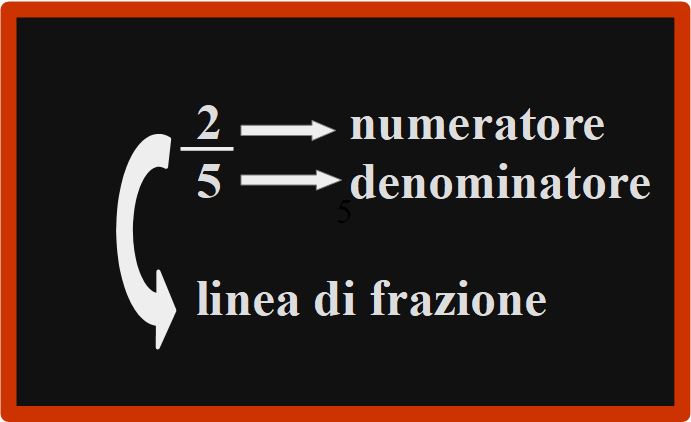
Nella frazione ![]()
- 2 è il numeratore e invece
- 5 è il denominatore. I due numeri sono separati dalla linea di frazione.
La frazione può essere letta in diversi modi:
- 2 su 5, oppure
- 2 fratto 5, oppure
- due quinti (mi raccomando non due alla quinta, che invece è la quinta potenza di due: 25 ).
Fatta questa necessaria premessa, passiamo alla somma tra frazioni.
Somma tra due frazioni con lo stesso denominatore
Esempio 1
Iniziamo sommando frazioni che hanno lo stesso denominatore e numeratore diverso (arriverai poi a saper sommare tre o più frazioni con denominatore diverso).
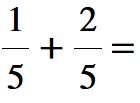
Le due frazioni hanno lo stesso denominatore, cioè 5, invece il numeratore è diverso. Nella prima frazione il numeratore è 1, nella seconda frazione è 2.
La regola dice questo:
“La somma di due frazioni che hanno lo stesso denominatore, è una frazione che ha per denominatore lo stesso denominatore e per numeratore la somma dei numeratori“.
È necessario più tempo per scrivere la regola che per applicarla.
Nella pratica dobbiamo riscrivere il denominatore e come numeratore mettiamo la somma dei numeratori (1 + 2 = 3).
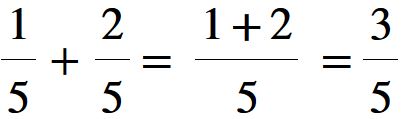
Il nostro risultato è 3 su 5, oppure si può leggere tre quinti. Mi raccomando non 3 alla quinta.
Tutto qui. Finito. Ti sembra troppo facile? Che tu ci creda o no, è così.
Possiamo aiutarci anche con un modello.
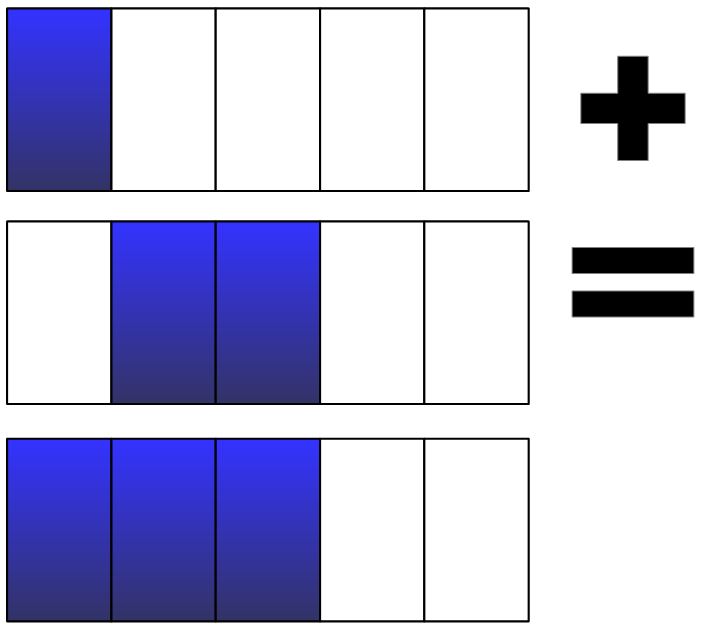
Esempio 2
Facciamo un altro esempio con i numeri. Consideriamo sempre due frazioni che hanno lo stesso denominatore, ma numeratore diverso; sette tredicesimi e tre tredicesimi.
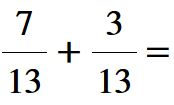
Per effettuare la somma, si riscrive una frazione che ha lo stesso denominatore e come numeratore mettiamo la somma dei numeratori (7 + 3 = 10).
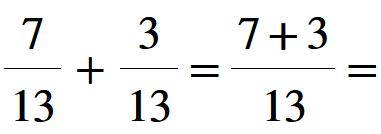
Quindi il risultato della somma è:
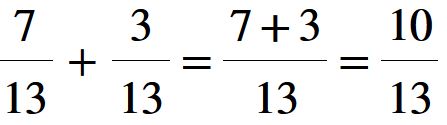
Il risultato della somma è 10 fratto 13, oppure dieci tredicesimi. Non 10 alla tredicesima. Tutto qua. Esercizio concluso.
Esempio 3
Facciamo ancora un altro esempio, aiutandoci con un modello. Due settimi + quattro settimi.
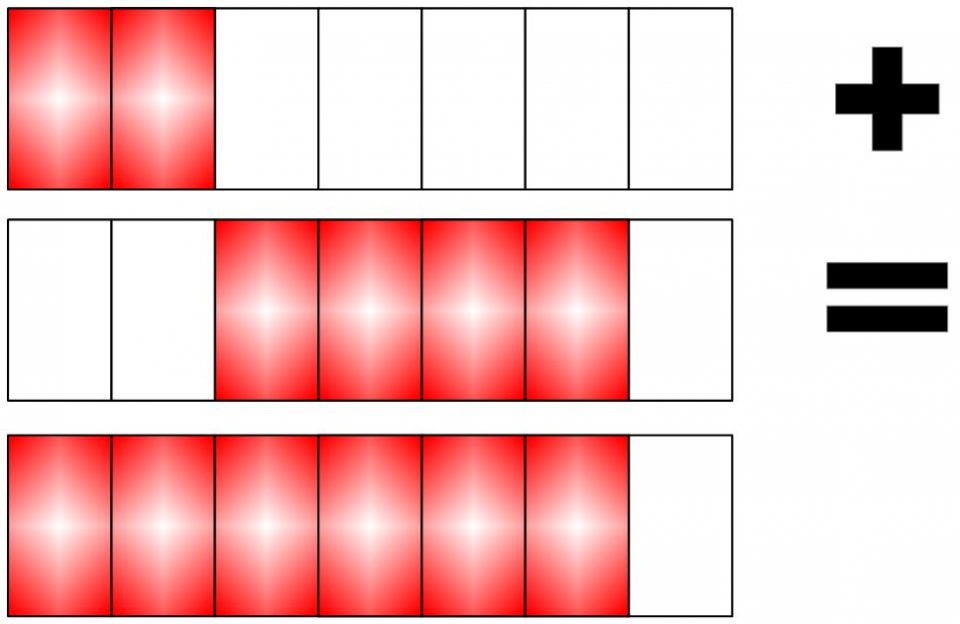
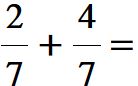
La somma delle due frazioni è una frazione che ha lo stesso denominatore (cioè 7) e come numeratore la somma dei numeratori (cioè 2 + 4 = 6)
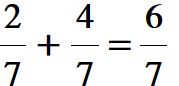
Il risultato che stavamo cercando è 6 fratto 7 oppure si può leggere sei settimi.
Esempio 4
Naturamlmente è anche possibile sommare 3 frazioni. Il procedimento è identico. Magari un po’ più lungo, ma il ragionamento è lo stesso.
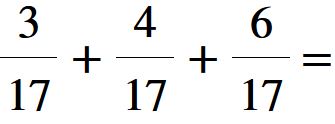
La somma sarà una frazione che avrà lo stesso denominatore delle frazioni di partenza (quindi 17) e come numeratore la somma dei tre numeratori (3 + 4 + 6 = 13).
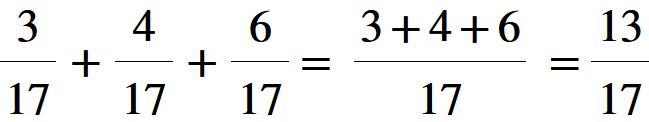
Il risultato che stavamo cercando è 13 su 17 oppure si può leggere tredici diciassettesimi. Esercizio concluso.
Esempio 5
Ancora un esempio con tre frazioni.
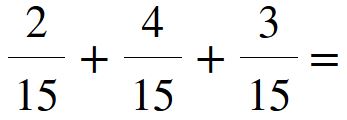
Come sopra, per ottenere la somma dobbiamo riscrivere lo stesso denominatore (15) e mettere come numeratore la somma dei numeratori (2 + 4 + 3 = 9).
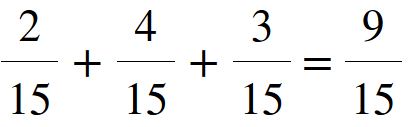
Abbiamo ottenuto come risultato 9 fratto 15 oppure si può leggere nove quindicesimi.
Dobbiamo fare attenzione perchè non abbiamo ancora finito. Come ti avrà detto sicuramente la tua prof, quando è possibile bisogna sempre ridurre ai minimi termini (dividere numeratore e denominatore per lo stesso numero).
Nel nostro esercizio, possiamo e dobbiamo dividere il 9 (numeratore) e il 15 (denominatore) per 3, ottenendo il risultato che puoi leggere sotto, cioè tre quinti.
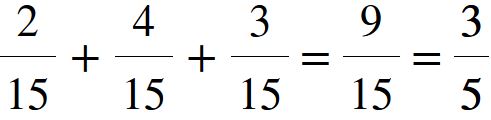
Esempio 6
Fino ad ora abbiamo ottenuto sempre come risultato delle frazioni proprie. Ma capita spesso di ottenere frazioni improprie. Vediamo un esempio.
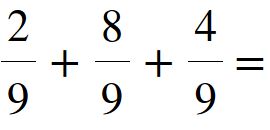
Il procedimento da seguire è lo stesso delle somme pecedenti. Otteniamo come risultato:
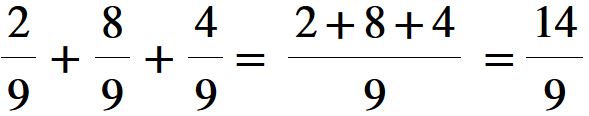
Quattordici noni è il nostro risultato.
Poichè il numeratore (14) è maggiore rispetto al denominatore (9), la frazione che abbiamo ottenuto è una frazione impropria, ma questo non ha nessuna influenza sulla correttezza del risultato. È giusto così.
Sottrazione tra frazioni con lo stesso denominatore
Tutto quello che abbiamo detto per l’ addizione tra frazioni con lo stesso denominatore, vale anche per le sottrazioni. Facciamo subito un esempio numerico.
esempio 7
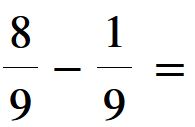
Il risultato di questa sottrazione è una frazione che ha come denominatore lo stesso denominatore e come numeratore la differenza dei numeratori.
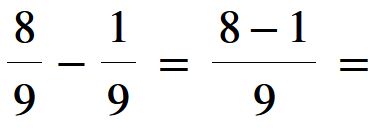
Eseguendo la differenza otteniamo
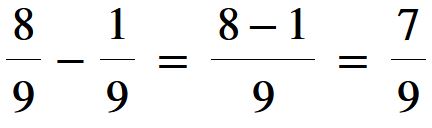
Il risultato che stavamo cercando è sette noni che si può anche leggere 7 su 9. Finito.
Esempio 8
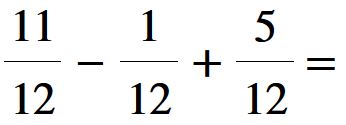
In questo caso abbiamo sia una sottrazione che un’addizione. Ma il procedimento non cambia. Procediamo come prima:
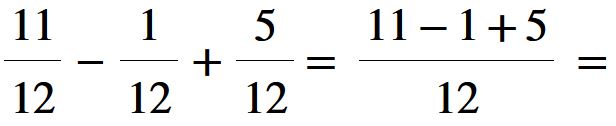
Eseguiamo le operazioni che troviamo al numeratore.
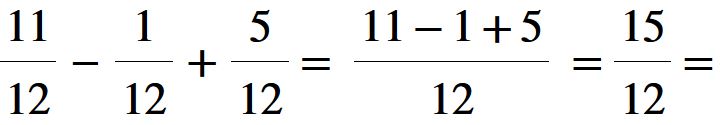
Come sempre, quando è possibile dobbiamo ridurre ai minimi termini, cioè dividere sia il numeratore che il denominatore per lo stesso numero. In questo caso dividiamo per 3 e otteniamo
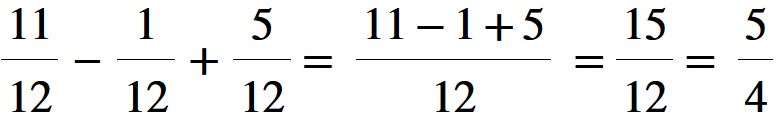
Cinque quarti è il risultato che stavamo cercando.
Esempio 9
Facciamo ancora un altro esempio. Ricorda, esercitarsi è il modo migliore per riuscire a svolgere bene gli esercizi. Non ti preoccupare se all’inizio ti sembra di impiegare troppo tempo. È normale. Solo con la pratica si diventa veloci e si sbaglia di meno. Ma andiamo al nostro nono esempio.
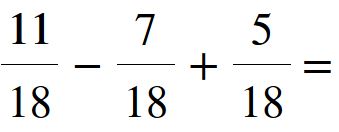
Sommiamo i numeratori e scriviamo lo stesso denominatore.
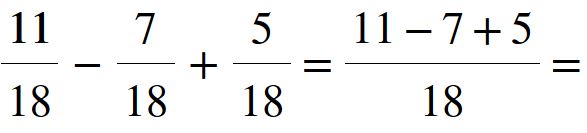
Eseguiamo le operazioni al numeratore.
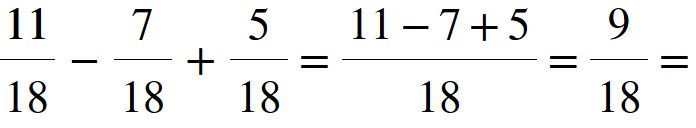
Abbiamo ottenuto come risultato nove diciottesimi. Come sempre quando è possibile bisogna ridurre ai minimi termini. In questo caso è possibile dividere il numeratore e il denominatore per 9.
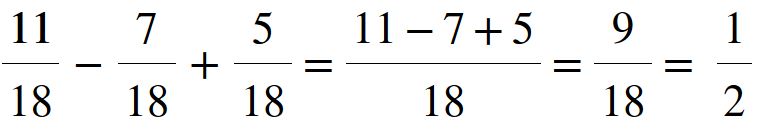
Il risultato che otteniamo è uno su due che si può leggere anche un mezzo. Finito.
Esercizi
Adesso possiedi gli strumenti che ti permettono di addizionare e sottrarre le frazioni che hanno lo stesso denominatore. Se vuoi puoi esercitarti con gli esercizi che leggi in basso. Lavora senza fretta e anche se sbagli non ti preoccupare. Sbagliando si impara.

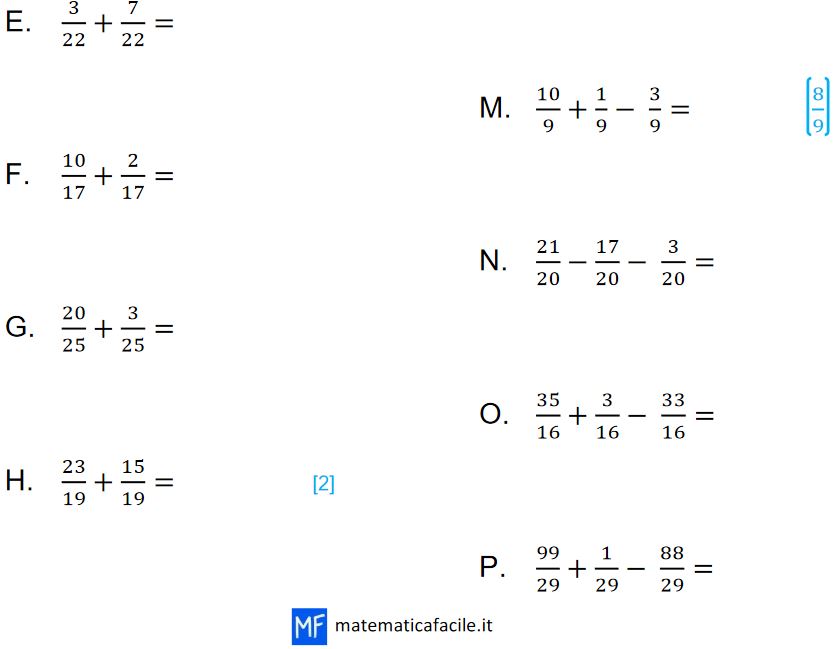
Buon lavoro.
A questo link della Casa Editrice Zanichelli trovi le tavole numeriche, le puoi solo consultare oppure puoi anche scaricarle come file pdf sul tuo pc per averle sempre a disposizione anche quando sei off-line.
Realizzare dei contenuti privi di errori è impossibile. Saremo grati ai lettori che vorranno segnalarci eventuali errori che abbiamo commesso nella stesura dell’articolo. Potete segnalarceli scrivendo alla casella mail: matematica.facile@libero.it