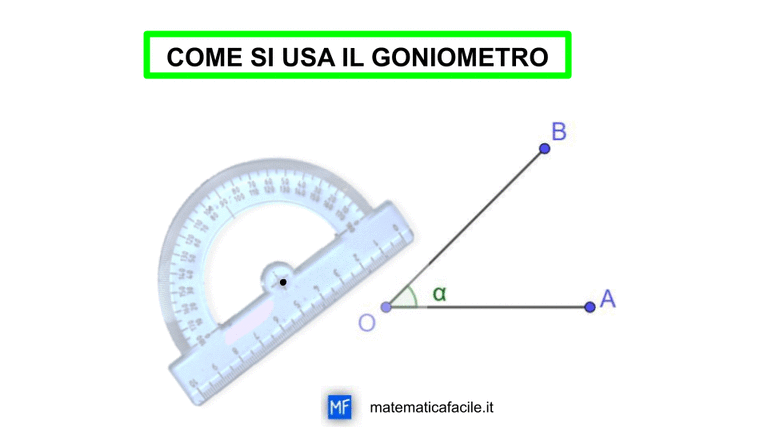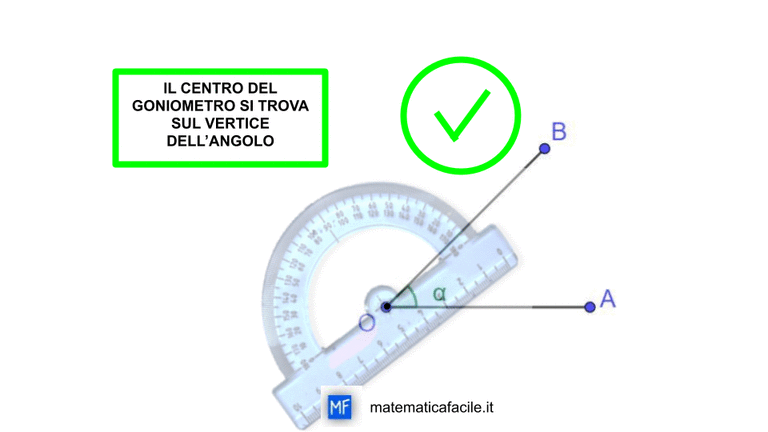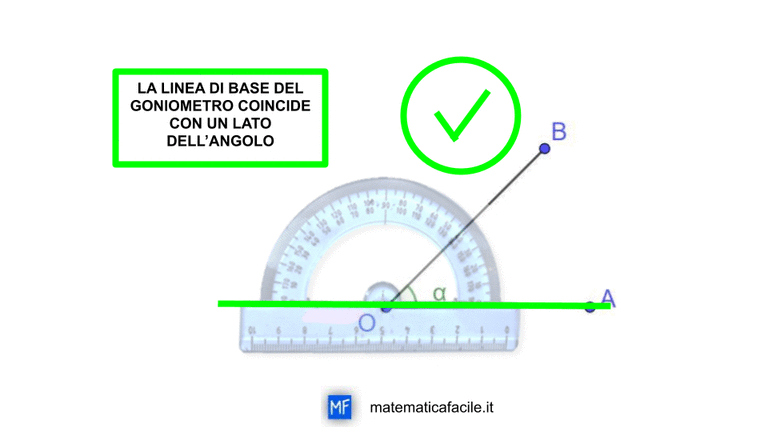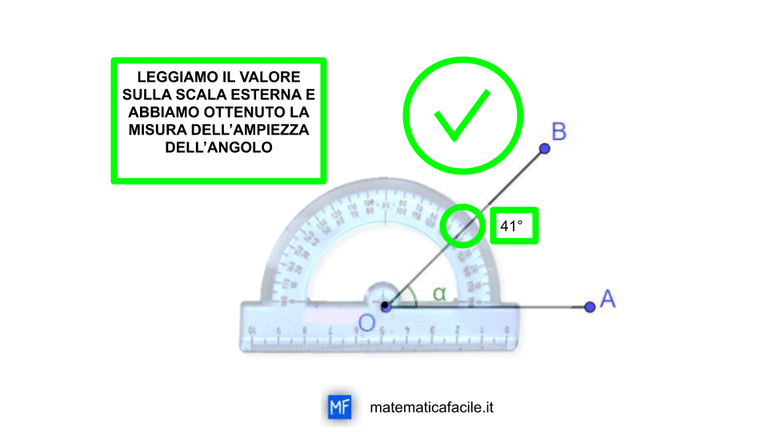
Oggi la prof di matematica ha spiegato le equazioni, ma tu non eri molto attento. Ora sei a casa e non sai da dove cominciare. Niente paura, con 5 minuti di impegno, saprai come si risolve un’equazione di primo grado. Cominciamo a fare i primi passi nel mondo delle equazioni con qualche esempio numerico.
Indice
- Primo esempio: primo membro e secondo membro
- Secondo esempio: termini incogniti e termini noti
- Regola del trasporto
- Verifica della soluzione
- Esercizi in pdf
- Esempio su Youtube – Iscriviti al nostro canale
Esempio 1 – Primo membro e secondo membro
Cominciamo con il nostro primo esempio per capire come si risolve un’equazione di primo grado.
Quando ci troviamo di fronte un’equazione, lo scopo del nostro lavoro è capire quale valore dare alla incognita (di solito si usa la lettera “x“, ma nessuno ti potrebbe vietare di usare la “w”) per far in modo che l’equazione sia verificata. Chiaro? No.
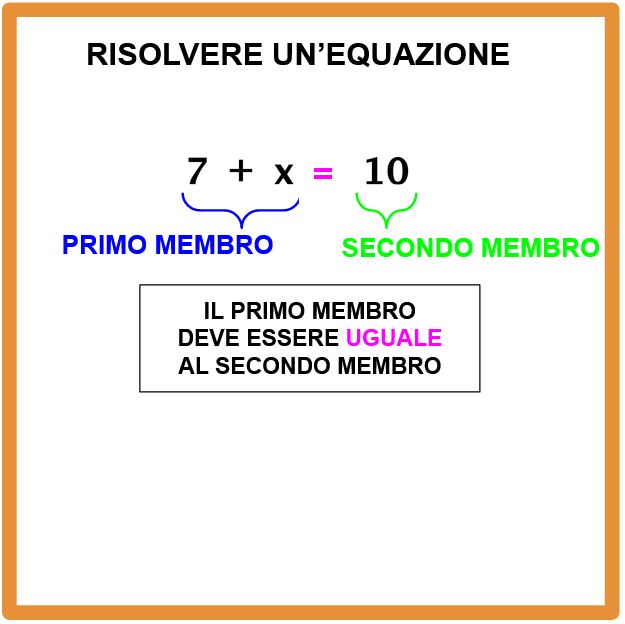
È naturale che non sia chiaro. Passiamo ai numeri e tutto diventerà più luminoso. Guardiamo la lavagna in basso.

La nostra equazione si legge sette più x uguale dieci.
Quello che ci chiediamo è:
“Quale valore devo dare alla x per fare in modo che quello che c’è scritto prima del segno dell’uguale
(cioè 7 + x)
abbia lo stesso valore di quello che c’è scritto dopo l’uguale
(cioè 10) ?
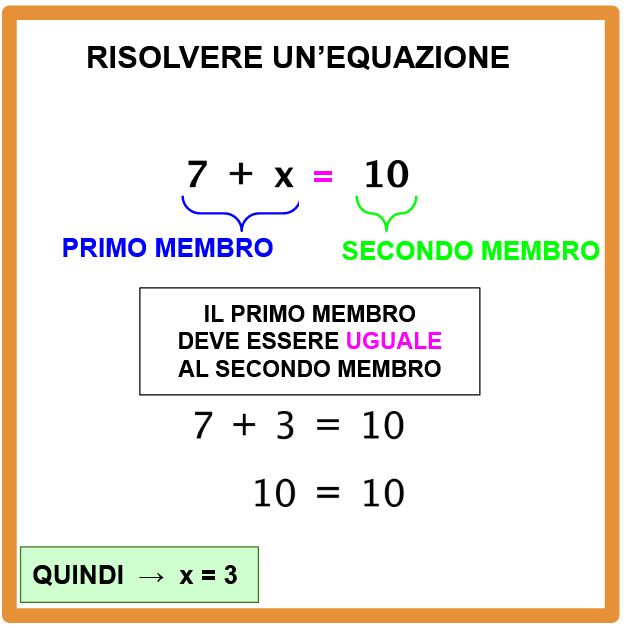
Quale valore devo dare alla x? La risposta non è poi così complicata. Il valore da attribuire alla x è 3. Infatti:
7 + 3 = 10
e quindi
10 = 10
Ed ecco che la nostra equazione è verificata.
Si dice che:
- l’equazione è verficata per x= 3 oppure
- la soluzione dell’equazione è x = 3.
Esempio 2 – termini incogniti e termini noti
Sfortunatamente, non sempre le equazioni sono così semplici. Facciamo un altro per capire come si risolve un’equazione di primo grado. Guardiamo la lavagna sotto.
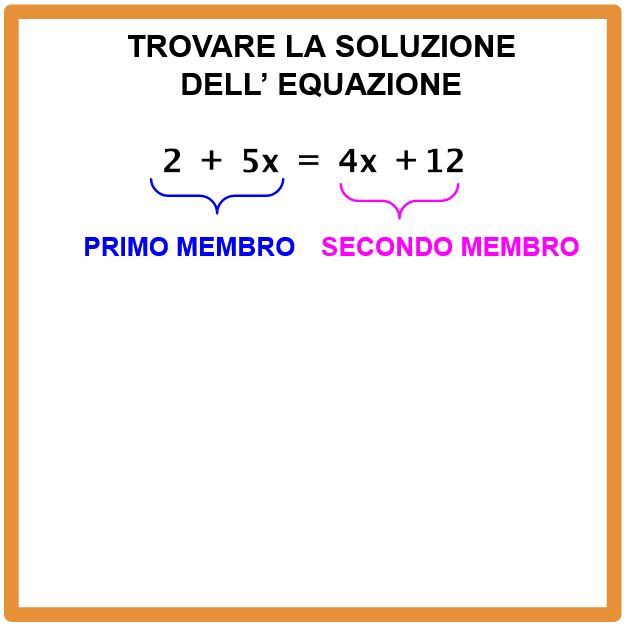
Ricordiamo che tutto ciò che si trova prima dell’uguale si chiama primo membro e invece tutto ciò che si trova dopo l’uguale si chiama secondo membro.
Per risolvere questa equazione però abbiamo bisogno di introdurre qualche altro nome. Dobbiamo imparare a individuare i termini incogniti e i termini noti. Fidati, non è nulla di difficile.
I termini incogniti sono quelli cha hanno la x
invece
i termini noti sono quelli che non hanno la x, cioè sono solo numeri.
Andiamo a individuare i termini incogniti e quelli noti nel nostro esempio.
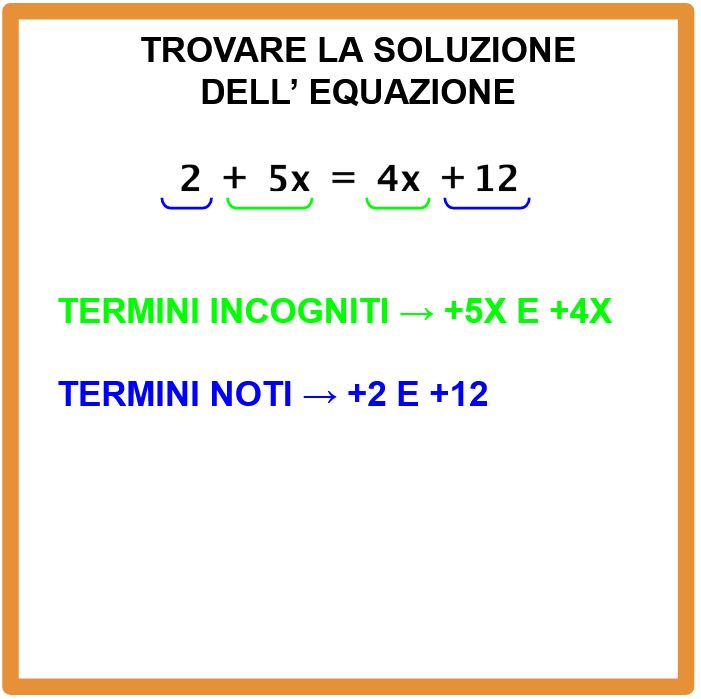
Come vedi, niente di difficile. I termini incogniti sono:
- 5x e 4x
invece i termini noti sono:
- +2 e +12
Una volta che abbiamo individuato i termini incogniti e quelli noti, siamo quasi a metà strada.
Regola del trasporto
Adesso dobbiamo applicare la regola del trasporto. Questa regola ci dice che per risolvere un’equazione:
è conveniente avere tutti i termini incogniti al primo membro e tutti i termini noti al secondo membro.
Facciamo le cose un passo alla volta. Cominciamo dai termini incogniti. Li vogliamo tutti al primo membro.
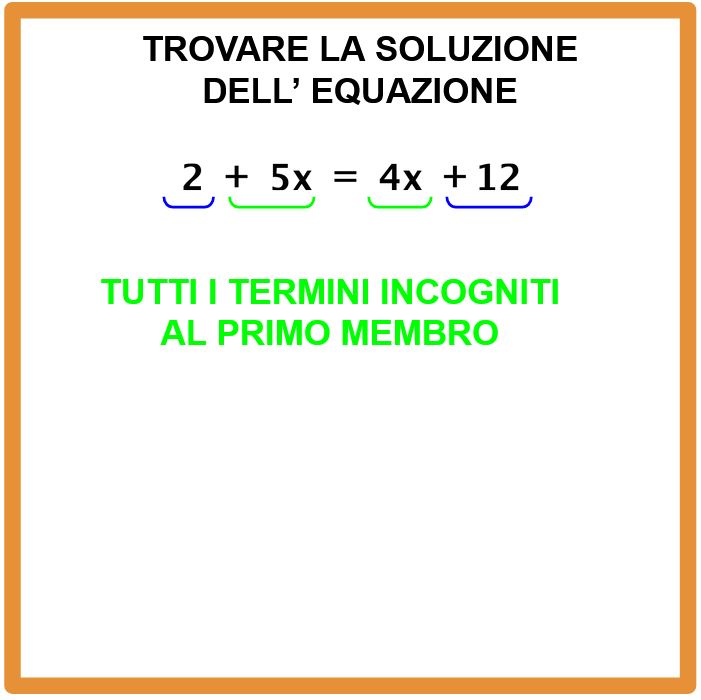
Il termine +5x si trova già al primo membro, quindi lo lasciamo lì tranquillo tranquillo.
Invece il termine 4x si trova al secondo membro. Per trasportarlo al primo membro dobbiamo cambiarlo di segno e quindi diventa -4x.
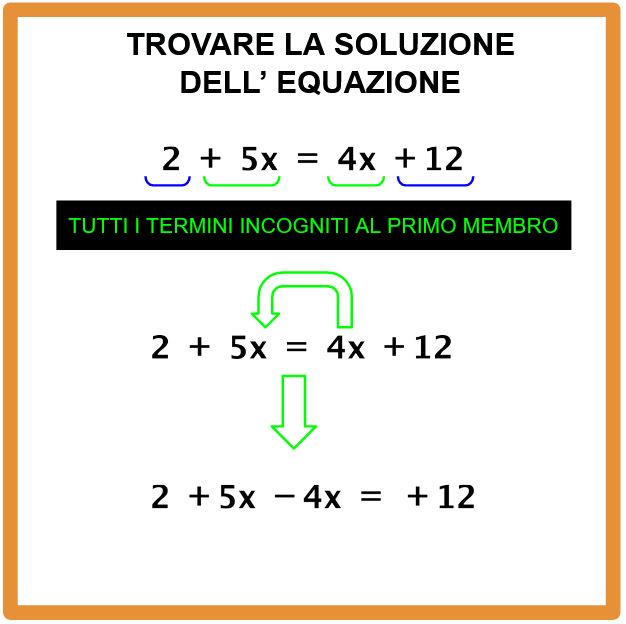
Adesso occupiamoci dei termini noti che devono essere tutti al secondo membro. Il termine +12 si trova già al secondo membro e lo lasciamo lì. Invece il +2 si trova al primo membro e dobbiamo trasportarlo al secondo membro, ma per trasportarlo, dobbiamo cambiargli di segno, quindi diventerà -2.
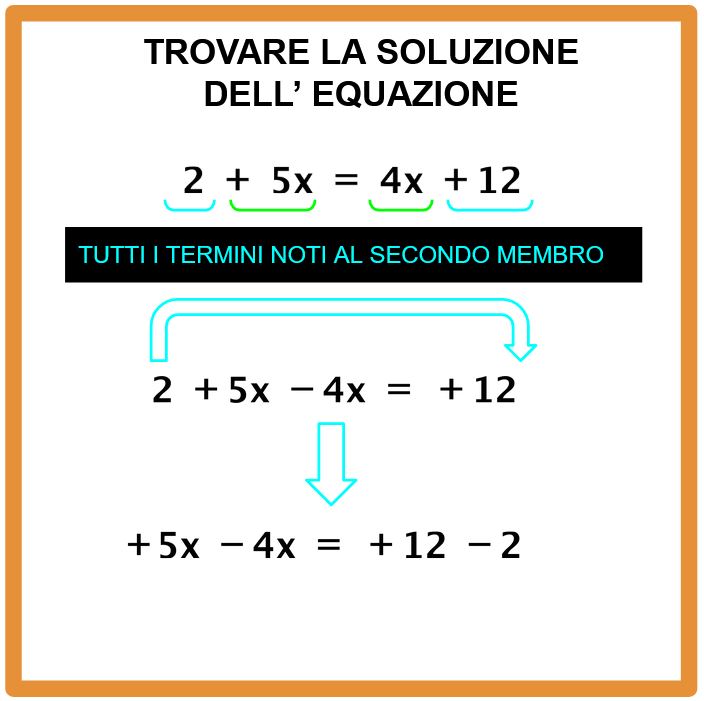
Siamo a un passo dalla fine dell’esercizio. Ora dobbiamo eseguire le operazioni che compaiono al primo membro e poi quelle che compaiono al secondo membro.
In particolare al primo membro abbiamo:
+5x -4x = 1x = x
E invece al secondo membro abbiamo:
+12 -2 = +10
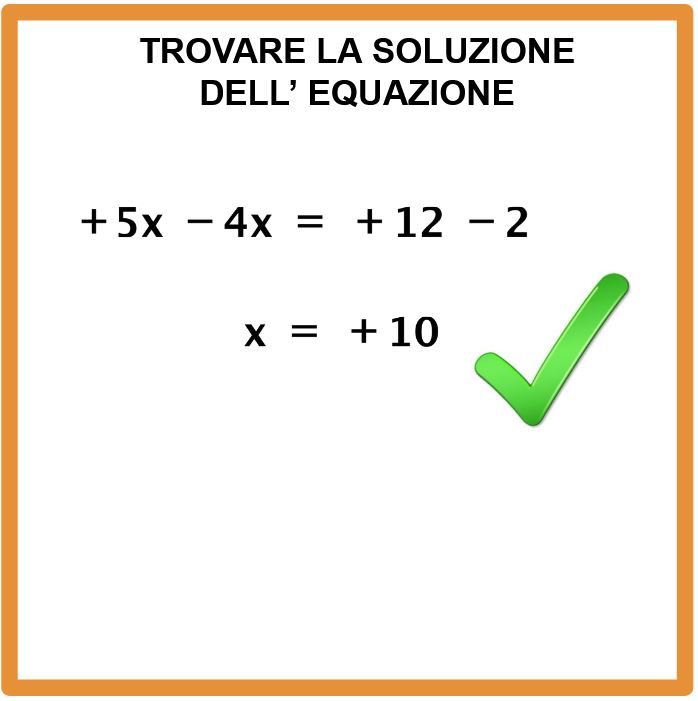
Quindi la soluzione (o radice) dell’equazione è
x = 10.
Esercizio concluso.
Verifica della soluzione
Ma siamo sicuri di avere lavorato bene? Come facciamo a sapere se nell’esercizio precedente la soluzione che abbiamo trovato sia quella giusta. Un metodo c’è, si chiama verifica dell’equazione. Quello che bisogna fare è andare a sostituire il 10 al posto della x nella equazione iniziale. È sempre meglio lavorare con i numeri.
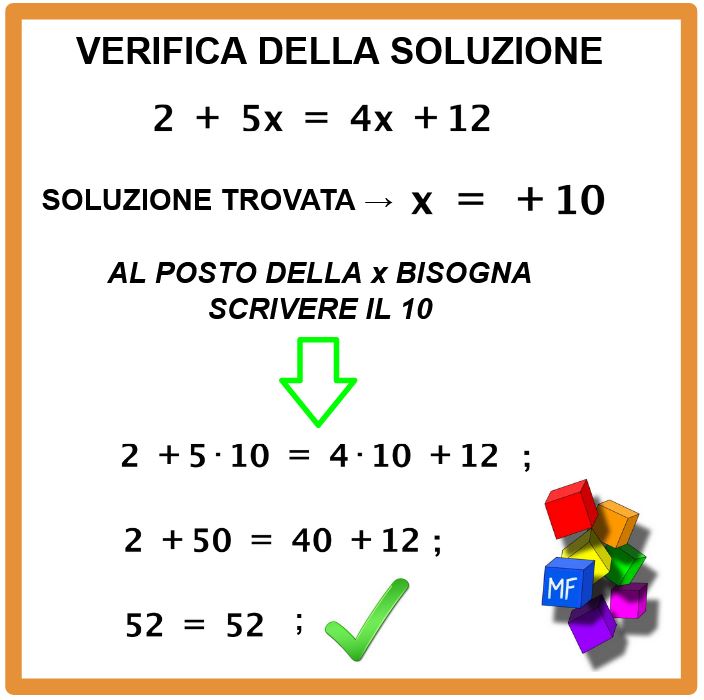
Fantastico, abbiamo trovato che 52 = 52. Questo vuol dire che la soluzione che abbiamo trovato era quella giusta.
Se avessimo trovato per esempio 54 = 52, allora voleva dire che da qualche parte avevamo sbagliato.
Esercizi in pdf
Adesso se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. I risultati ti servono per capire se hai lavorato bene. Non avere fretta di finire, lavora con calma e non preoccuparti se sbagli. Sbagliando si impara.
![]() Equazioni: primi passi – Esercizi.pdf
Equazioni: primi passi – Esercizi.pdf
Buon lavoro.
ESEMPIO SU YOUTUBE
A questo link della Casa Editrice Zanichelli potrai consultare e scaricare liberamente le tavole numeriche in formato pdf, in modo da averle sempre a disposizione anche quando sei off-line.
Se vuoi porre domande o vuoi segnalare un errore puoi contattarci attraverso le nostre pagine social oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori.