Ti sei chiesto a cosa serve il Teorema di Pitagora e non riesci a darti a una risposta? In questo articolo vedremo il Teorema di Pitagora applicato al parellelogramma ( si può anche chiamare parallelogrammo). Naturalmente le occasioni in cui conoscere Pitagora saranno molte, ma cominciamo con le cose semplici. Facciamo subito un esempio numerico.
E se non l’hai ancora fatto, iscriviti al mio canale YouTube matematicafacile.
Indice
Esempio 1
Guardiamo la figura in basso. Abbiamo un parallelogramma. Conosciamo le lunghezze di alcuni segmenti. Vogliamo sapere il perimetro e l’area del parallelogramma.
Ricordiamoci che:
- il perimetro è la somma di tutti i lati di un poligono e
- l’area del parallelogramma si calcola moltiplicando la lunghezza della base per la lunghezza dell’altezza → A = b · h
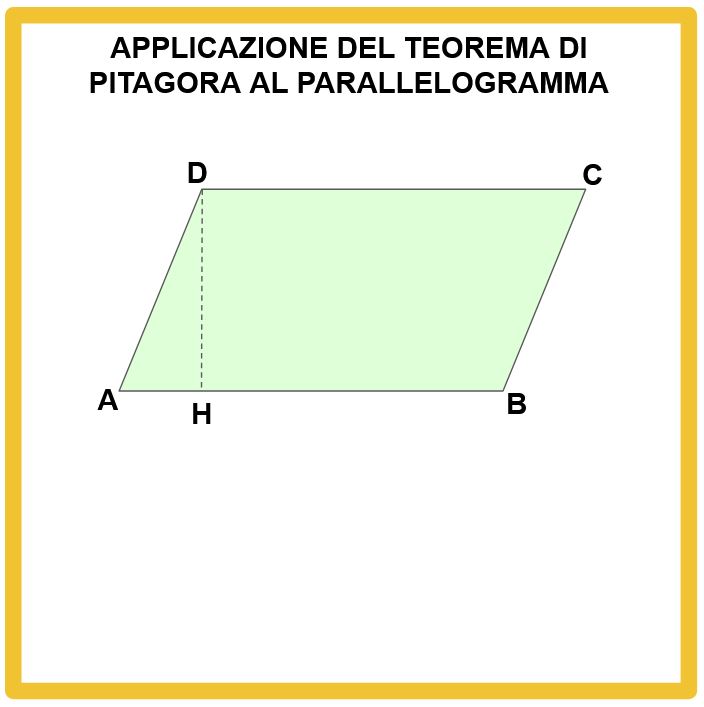
Nel nostro parallelogramma:
- il segmento AB è la base e
- il segmento DH è l’altezza.
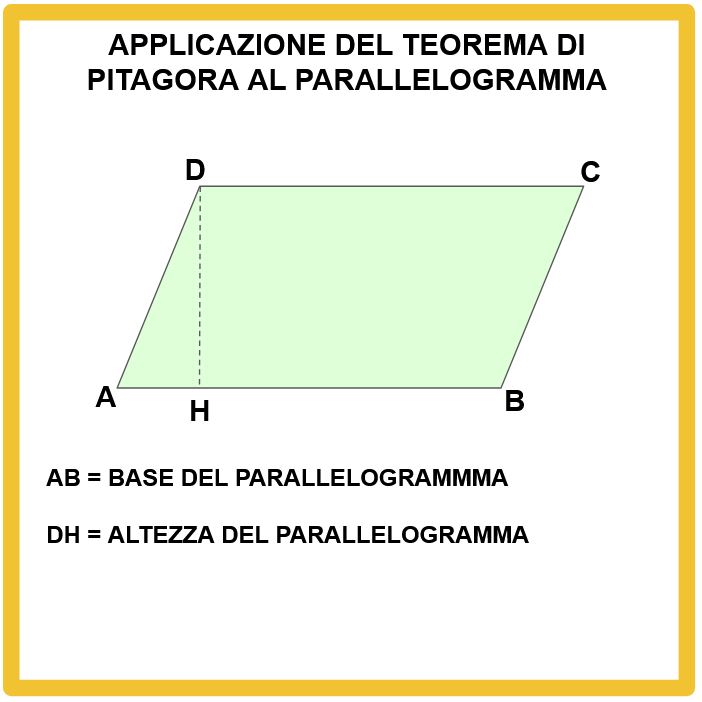
Leggiamo nella lavagna sotto quali sono i dati, cioè le misure che conosciamo. Ricordiamoci che il nostro scopo è determinare il perimetro e l’area del parallelogramma.
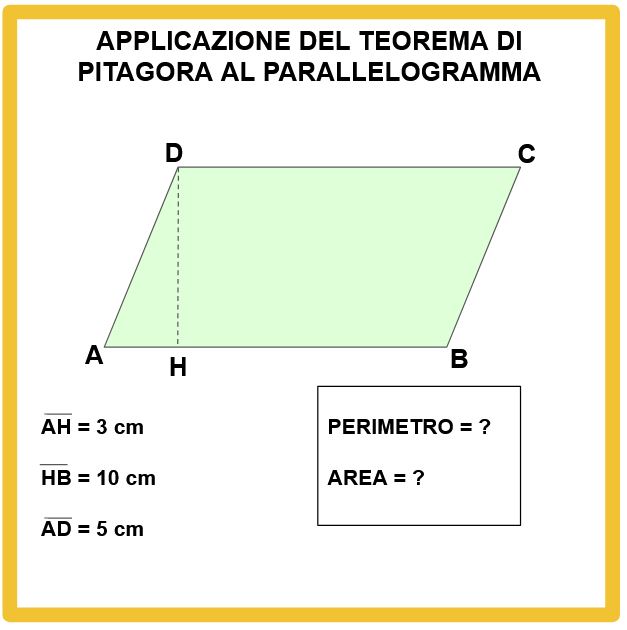
Calcolo del perimetro
Partiamo dalle cose facili. Iniziamo calcolando il perimetro.
Dato che abbiamo a che fare con un parallelogramma, i lati opposti sono uguali (come nel rettangolo).
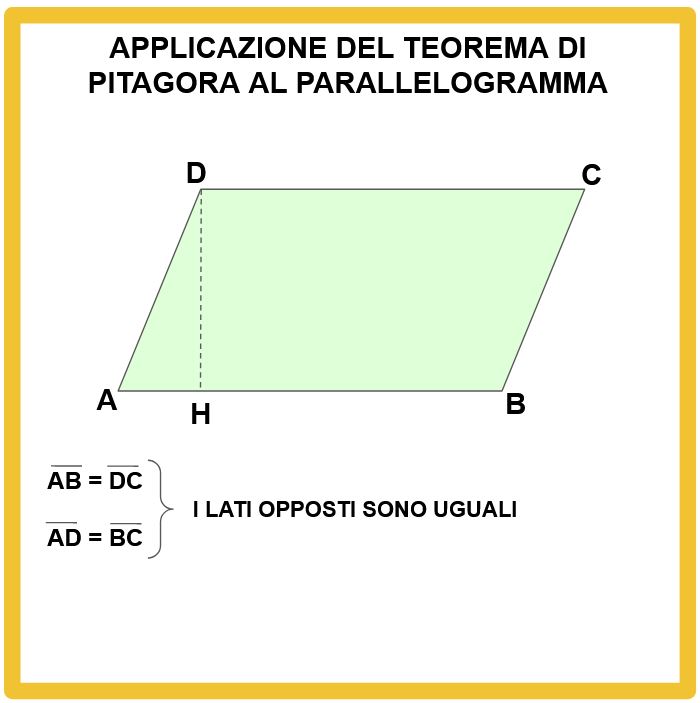
Molto bene, andiamo alle misure e ai calcoli.
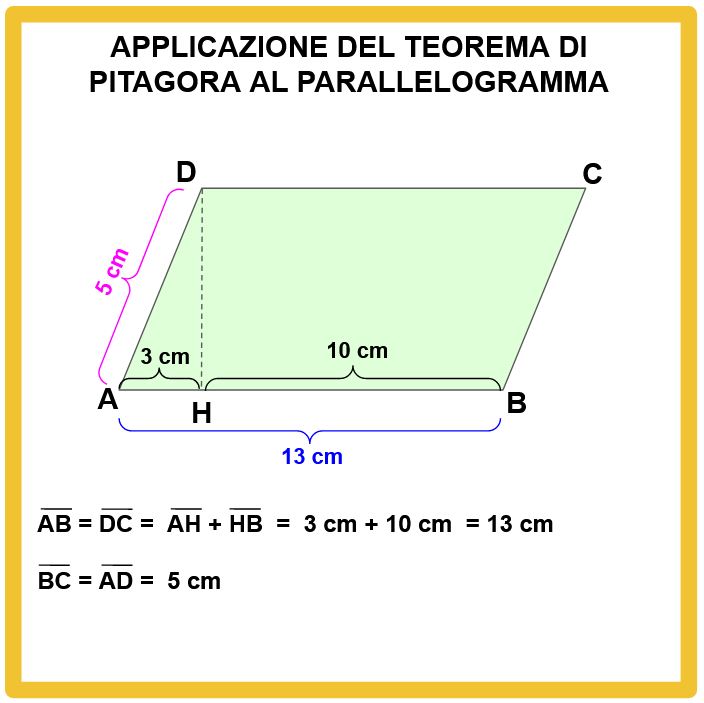
Adesso non dobbiamo fare altro che andare a sommare i 4 lati, di cui conosciamo la lunghezza e avremo ottenuto il perimetro.
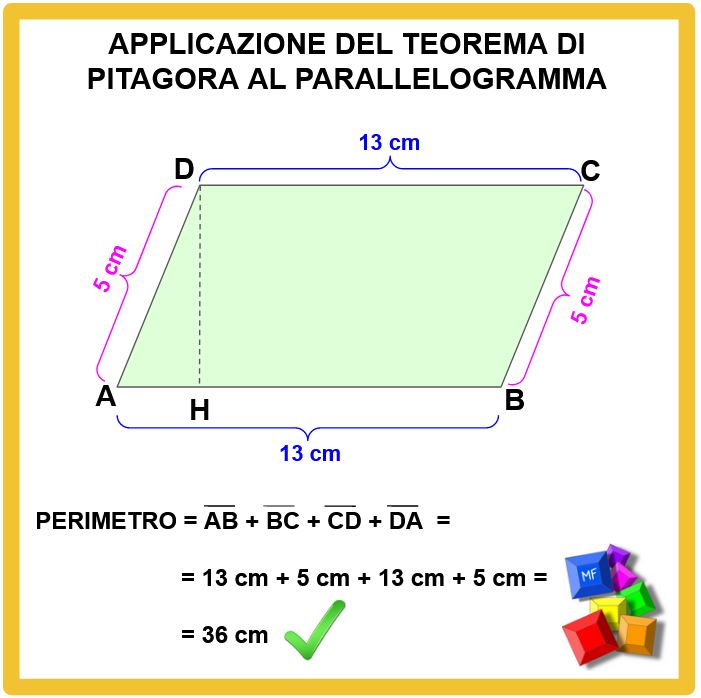
Il perimetro del nostro parallelogramma misura 36 cm.
E finora niente di troppo complicato. Adesso andiamo a determinare l’area.
Calcolo dell’area
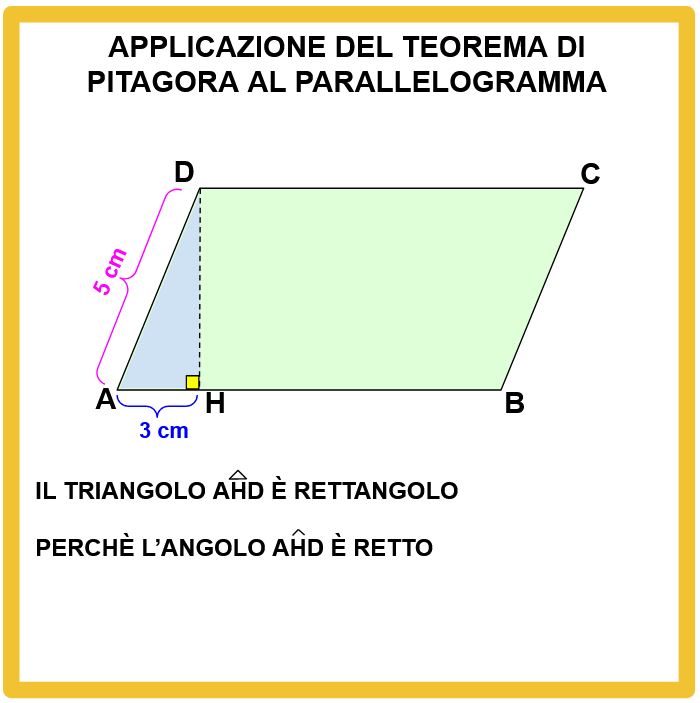
Per calcolare l’area abbiamo bisogno di sapere la misura dell’altezza. Per determinare l’altezza dobbiamo applicare il Teorema di Pitagora al triangolo rettangolo AHD.
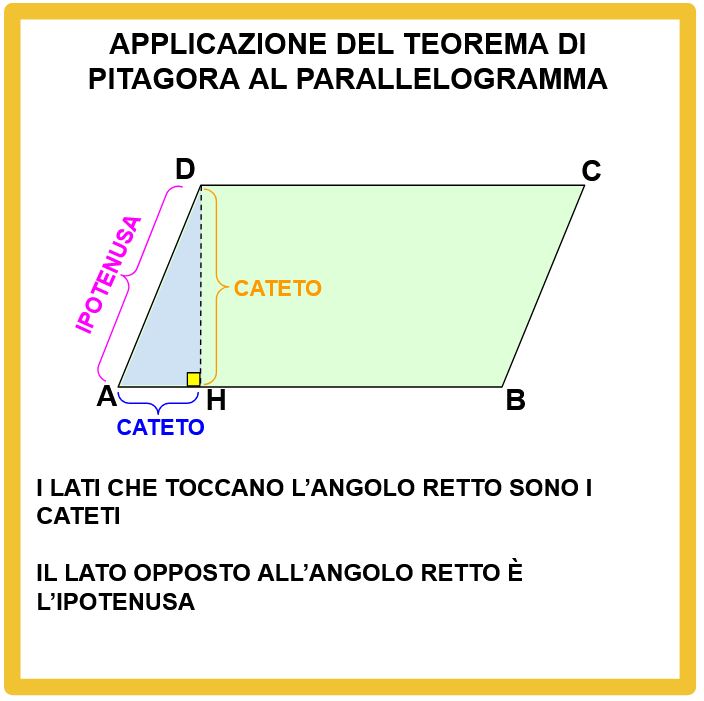
In qualsiasi triangolo rettangolo, i lati che toccano l’angolo retto sono i cateti. Invece il lato opposto all’angolo retto è l’ipotenusa.
Continuiamo con il Teorema di Pitagora applicato al parellelogramma. Nel nostro esempio conosciamo la lunghezza dell’ipotenusa e di uno dei cateti.
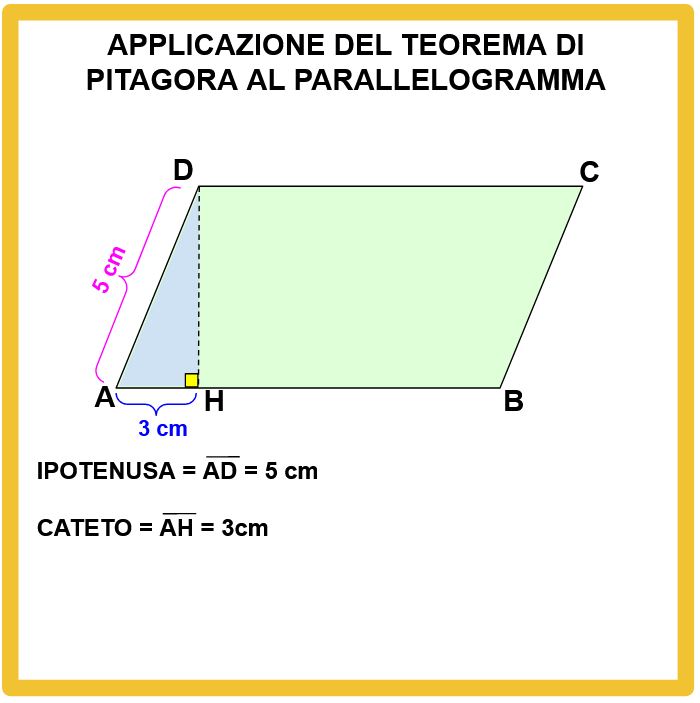
Per calcolare la lunghezza dell’altro cateto applichiamo Pitagora, come puoi vedere nella lavagna sotto.
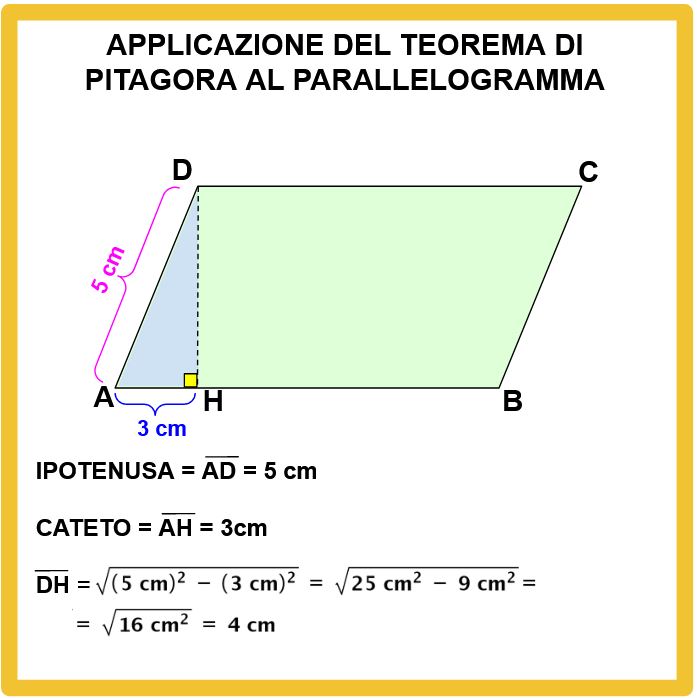
Abbiamo trovato che l’altezza del parallelogramma misura 4 cm. Adesso finalmente possiamo calcolare l’area.
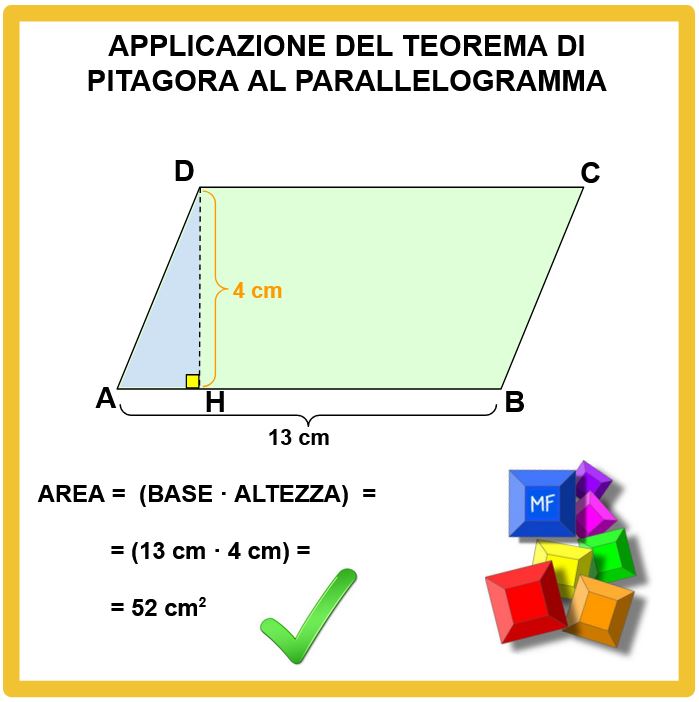
Esercizio concluso. L’area del parallelogramma misura 52 cm2 .
Esercizi in pdf
Adesso se vuoi, ti puoi mettere alla prova con gli esercizi che trovi nel file pdf sotto. Lavora con calma e non ti preoccupare se sbagli. Sbagliare è normale e sbagliando si impara.
Il Teorema di Pitagora applicato al parallelogramma – Esercizi.pdf
Buon lavoro.
Cliccando qui verrai indirizzato in un nuova pagina della Casa Editrice Zanichelli in cui potrai scaricare liberamente le tavole numeriche.
Se vuoi porre delle domande o vuoi segnalare un errore, puoi contattarci attraverso i nostri canali social oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori.
