In questo articolo vedremo l’utilità del Teorema di Pitagora per determinare l’area o il perimetro del rombo. Spesso ai prof capita di sentirsi chiedere: “Ma a cosa serve il Teorema di Pitagora?” Dando un’occhiata a questo articolo, capirai come il Teorema di Pitagora può essere applicato al rombo. Ma basta parlare, facciamo subito qualche esempio.
Indice
Il rombo e il triangolo rettangolo
Nella lavagna in basso vediamo un rombo i cui vertici si chiamano A, B, C e D.
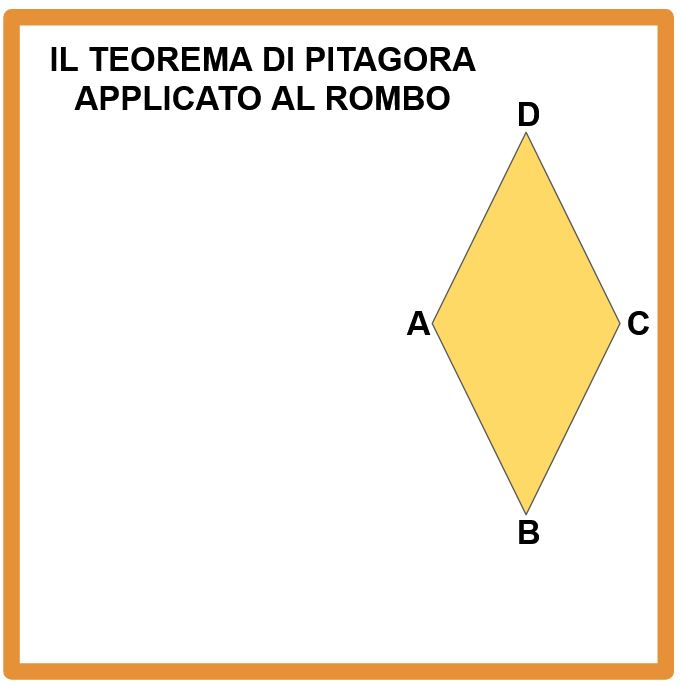
Per prima cosa tracciamo le due diagonali. Ti ricordo che:
“Una diagonale in un poligono è quel segmento che unisce due vertici non consecutivi”.
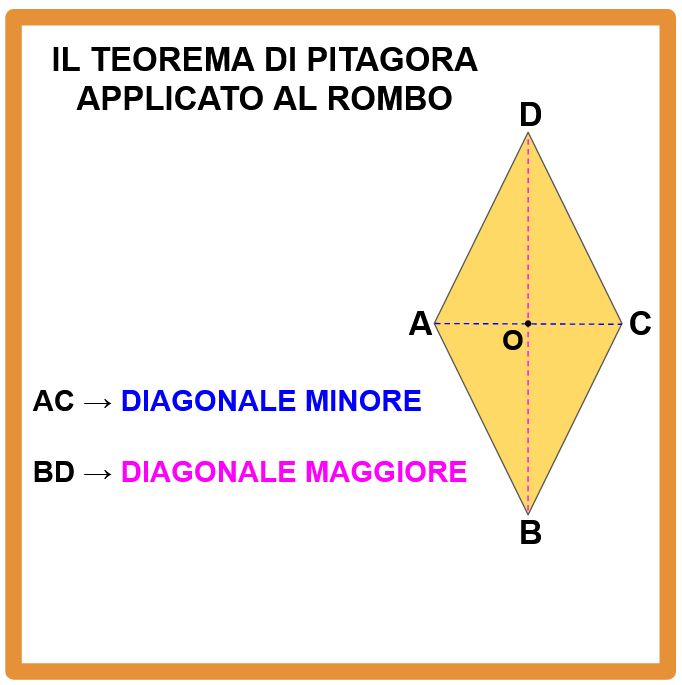
Nel rombo del nostro esempio, la diagonale minore è il segmento AC, si chiama minore perché è più corta dell’altra. Invece la diagonale maggiore è il segmento BD, si chiama maggiore perché è più lunga della diagonale minore. Nell’immagine il punto in cui le diagonali si incontrano è chiamato O. (Se le due diagonali fossero uguali, non avremmo più a che fare con un rombo, ma con un quadrato).
Una cosa molto importante da ricordare è che:
“Nel rombo le diagonali si incontrano perpendicolarmente”.
Detto in modo diverso, le due diagonali formano 4 angoli retti. A noi interessa solo uno di questi angoli retti.
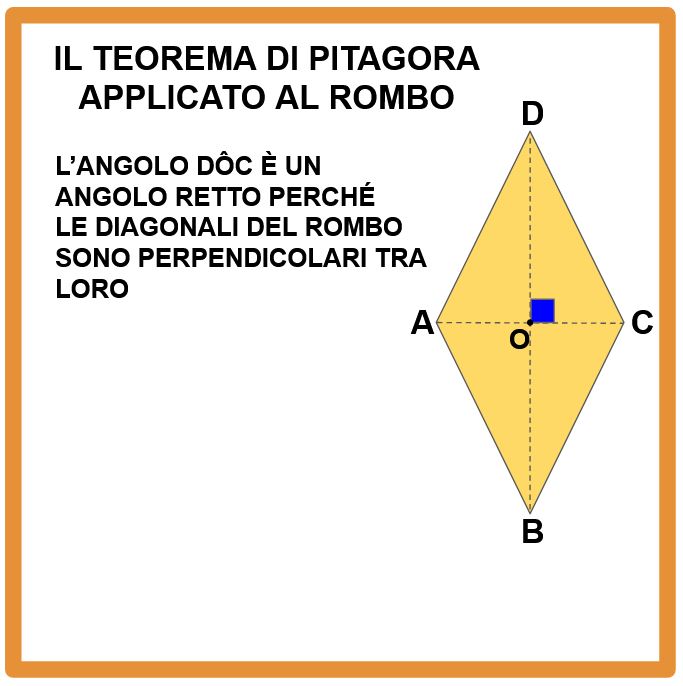
Se le diagonali sono perpendicolari allora, il triangolo DOC è un triangolo rettangolo.
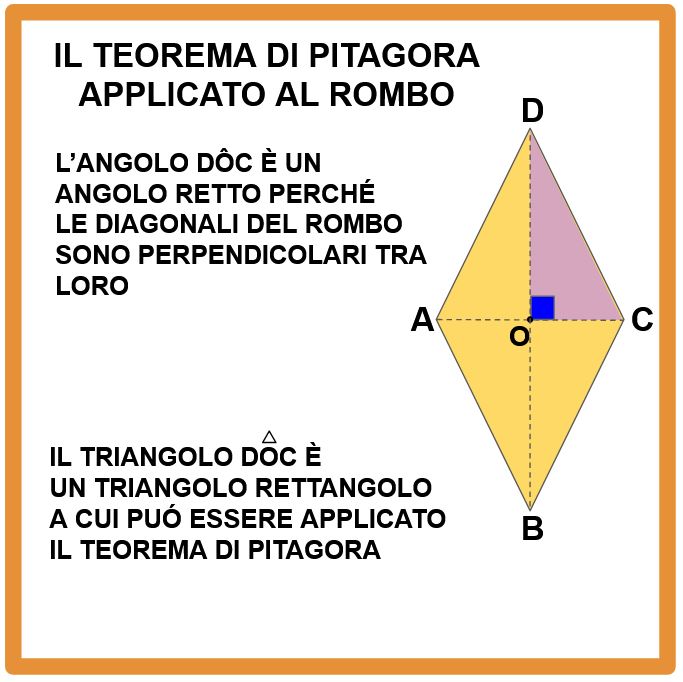
Molto bene, adesso che abbiamo individuato un triangolo rettangolo (il Teorema di Pitagora funziona solo con i triangoli rettangoli) dobbiamo ricordarci quali sono i cateti e qual è l’ipotenusa. Zoomiamo per vedere meglio i lati del triangolo.
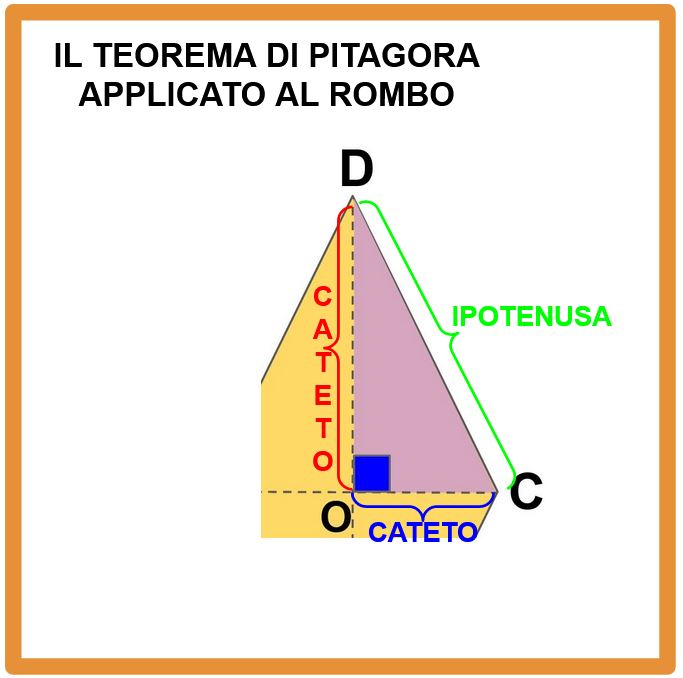
I lati che toccano l’angolo retto sono i cateti (forse la tua prof avrà detto ‘i lati adiacenti all’angolo retto‘). Invece il lato opposto all’angolo retto è l’ipotenusa.
Vediamo ora un problema che riguarda il Teorema di Pitagora applicato al rombo.
Esempio 1
Del rombo in figura conosciamo il perimetro e la diagonale maggiore. La consegna ci chiede di determinare l’area del rombo.
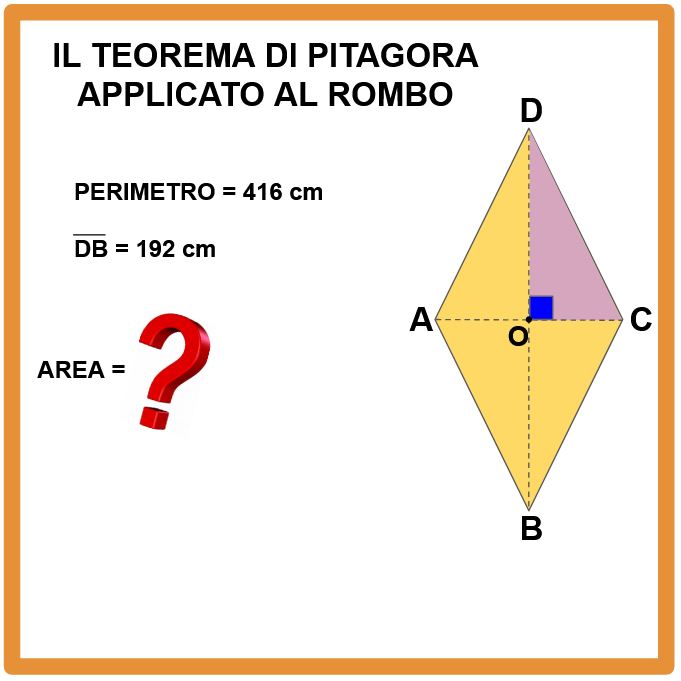
Riflettiamo, ragioniamo e andiamo con calma.
La consegna ci chiede di determinare l’area del rombo. Quindi la prima cosa che dobbiamo fare è andare a ricordarci come si calcola l’area del rombo. Così come in tutti i poligoni con le diagonali perpendicolari, l’area si calcola moltiplicando le diagonali tra loro e dividendo il risultato per due.
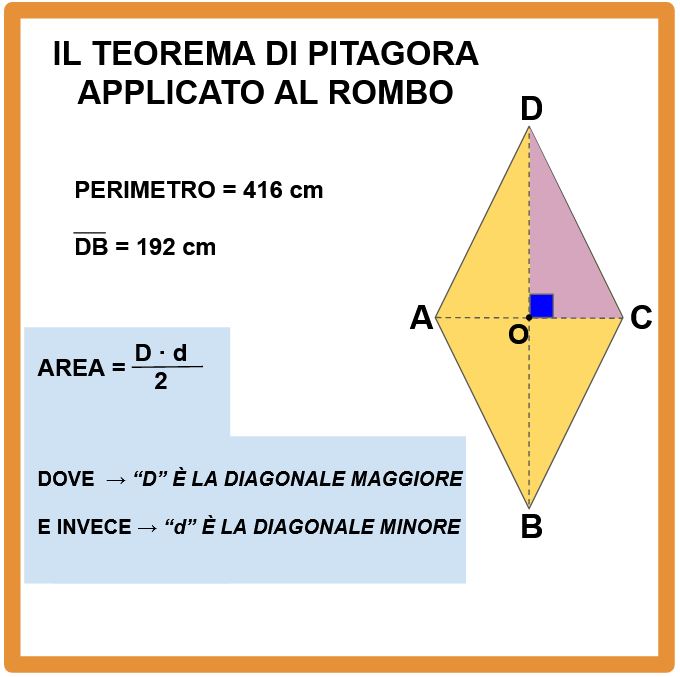
Bene. Abbiamo bisogno delle due diagonali. Quella maggiore ce l’abbiamo. Dobbiamo trovare il modo di ricavare la lunghezza della diagonale minore.
Sappiamo quanto misura il perimetro. Il perimetro è uguale alla somma di tutti i lati. Dobbiamo ricordare che nel rombo i lati sono tutti uguali (come nel quadrato).
Quindi dividendo il permetro in 4 parti troviamo la lunghezza di ogni lato. I calcoli li trovi nella lavagna sotto.
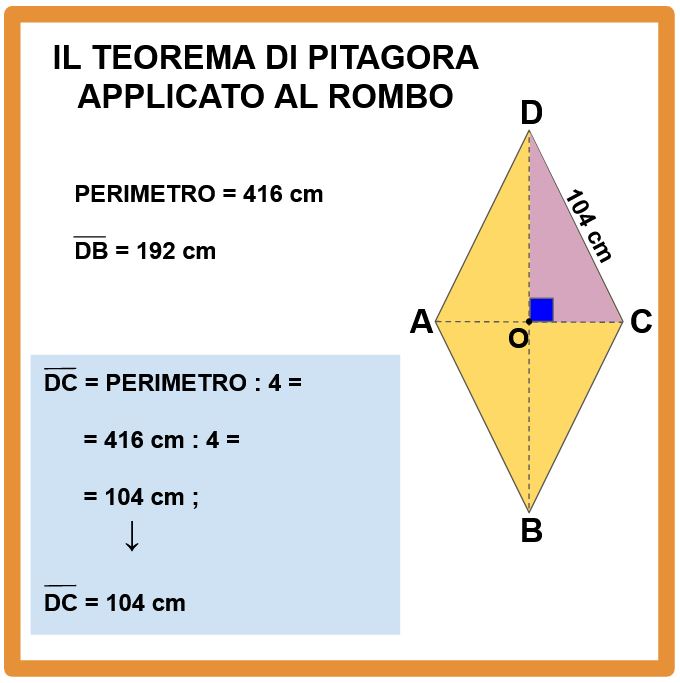
Abbiamo ottenuto che ogni lato misura 104 cm. In particolare ci interessa la lunghezza del lato DC perché è l’ipotenusa del triangolo rettangolo DOC.
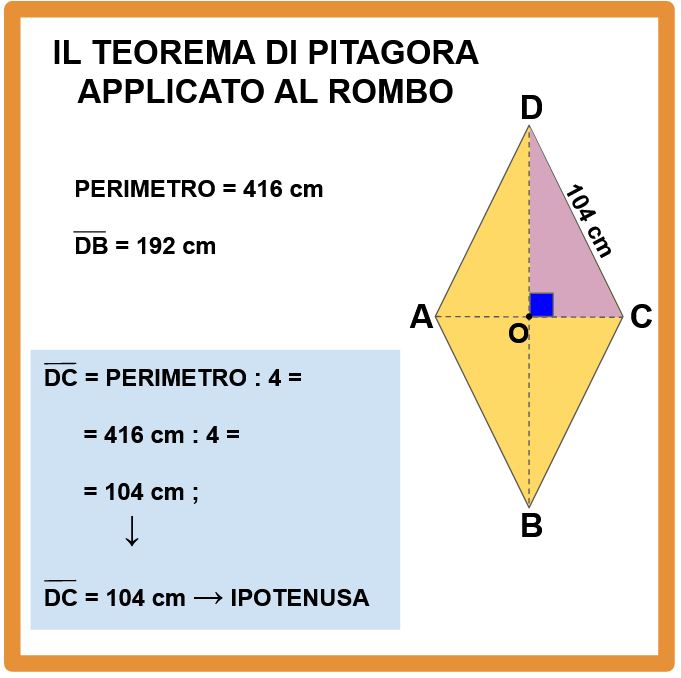
Di questo triangolo rettangolo però non conosciamo solo l’ipotenusa, ma anche uno dei due cateti.
Infatti, le diagonali del rombo si incontrano nel loro punto medio. Questo vuol dire che se tutta la diagonale DB misura 192 cm, il segmento OD è lungo la metà di DB. Per ricavare la lunghezza di OD dobbiamo dividere a metà DB.
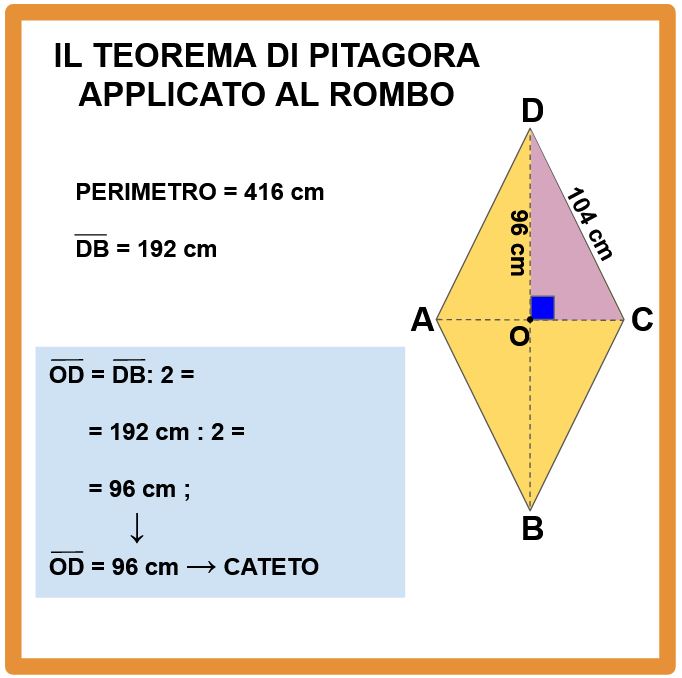
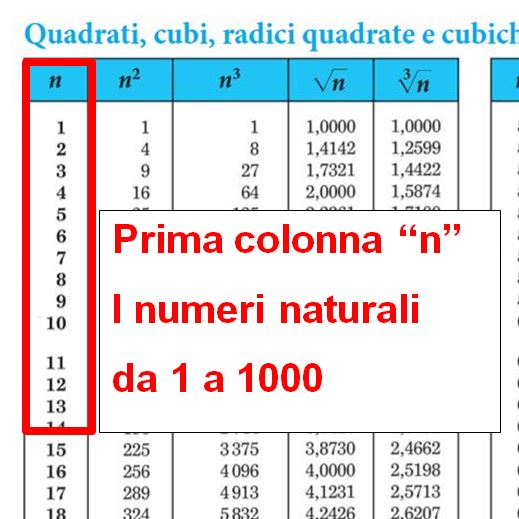
È arrivato il momento di applicare Pitagora. Infatti conoscendo l’ipotenusa DC e il cateto OD, possiamo ricavare l’altro cateto OC. Per i calcoli puoi usare la calcolatrice, ma sarebbe preferibile imparare a usare le tavole numeriche. Se non sai come si fa, potresti leggere il mio articolo come si usano le tavole numeriche. Se le hai perse, puoi scaricarle gratis cliccando qui.
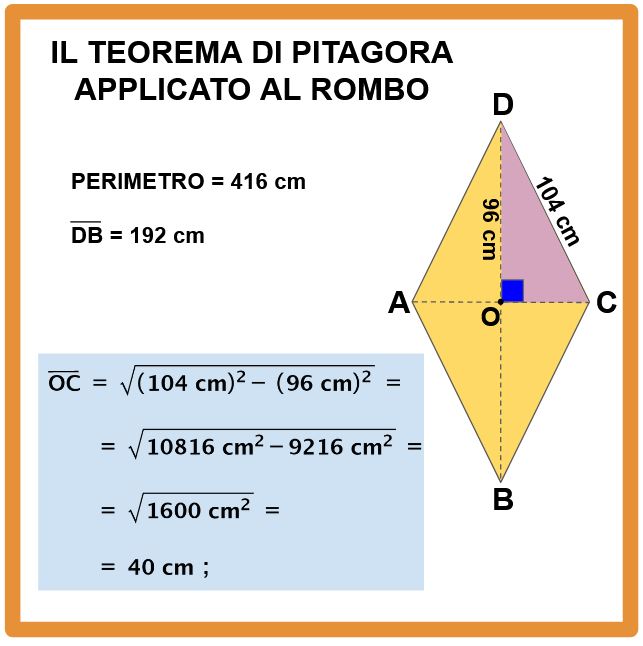
Dopo avere ottenuto OC, è sufficiente moltiplicarlo per 2 per ottenere la diagonale minore.
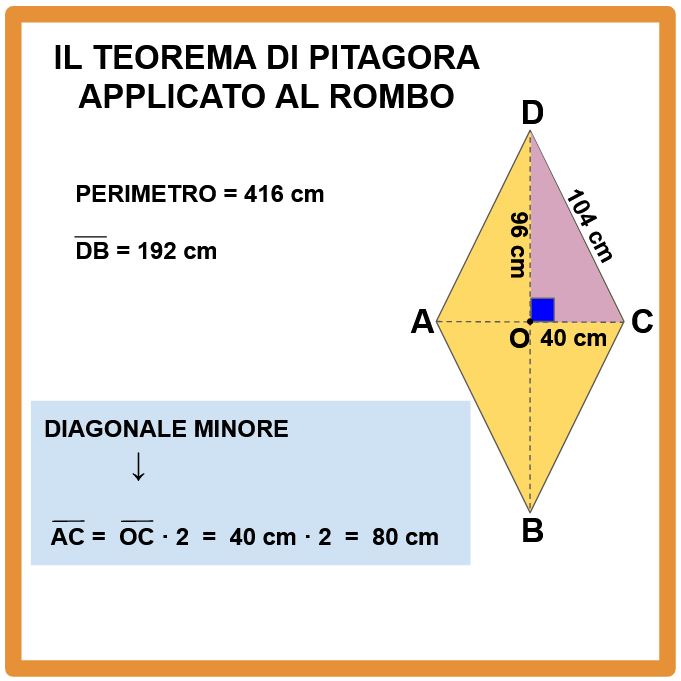
Adesso che abbiamo la diagonale maggiore e la diagonale minore, possiamo andare avanti con il teorema di Pitagora applicato al rombo e finalmente determinare l’area del rombo.
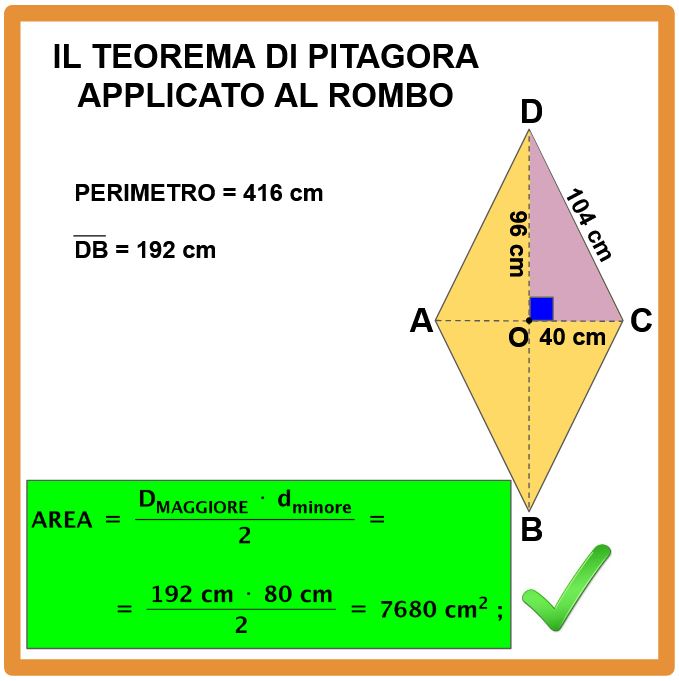
Abbiamo finito. L’area del rombo misura 7680 cm2.
Esercizi in pdf
Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Lavora con calma e senza fretta. I risultati ti servono per capire se hai lavorato bene.
![]() Il teorema di Piatagora applicato al rombo – Esercizi.pdf
Il teorema di Piatagora applicato al rombo – Esercizi.pdf
Buon lavoro.
Se vuoi porre delle domande o vuoi segnalare un errore, puoi contattarci attraverso le nostre pagine social oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori.
Su Youtube
Se preferisci vedere dei video invece che leggere un articolo, allora potresti iscriverti al mio canale Youtube.
Buongiorno,
nella definizione di ipotenusa (LEZIONE PITAGORA E ROMBO) manca la parola “opposto”.
Grazie per la segnalazione. Ho provveduto a correggere. 🙂