Oggi mentre la prof di matematica spiegava ha usato la parola “congruente”. Durante l’intervallo alcuni tuoi compagni dicevano che dire “congruenti” e dire “uguali” era la stessa cosa. Altri invece dicevano che sono due cose diverse. Tu non ci hai capito molto e sei finito in quest pagina. Dopo che avrai letto questo articolo spero che non avrai più dubbi su che differenza c’è tra uguale e congruente.
Indice
- Congruente si usa in geometria
- Il concetto di uguaglianza
- Il concetto di congruenza
- Uguali o congruenti ?
- Il simbolo di congruenza
- Il simbolo di uguaglianza
“Congruente” si usa in geometria
Una grande differenza è che la parola congruente si usa solo in geometria. In aritmetica la parola congruente non viene usata. Quindi questo ci fa capire che il concetto di congruente ha a che fare con la geometria, ma non con l’aritmetica.
Il concetto di uguaglianza
Partiamo dalle cose più semplici. La parola uguale viene usata in aritmetica (ma vedremo anche in geometria), per esempio nell’addizione:
2 + 2 = 4
usiamo la parola uguale e usiamo anche il simbolo di uguaglianza, cioè i due trattini sovrapposti → “=“.
Il simbolo = di uguaglianza vuol dire che la quantità che c’è a sinistra dell’uguale deve essere uguale alla quantità che si trova a destra. Ma queste sono cose che abbiamo imparato alle elementari:
2 · 5 = 10
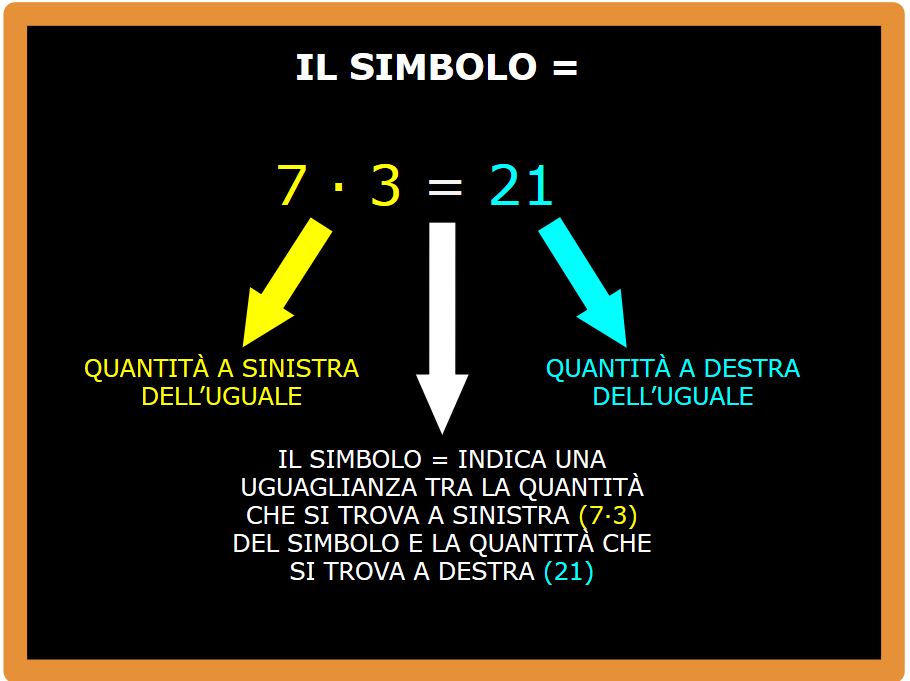
Credo che sul simbolo uguale = e sul significato di uguaglianza siamo tutti d’accordo. Passiamo al concetto di congruente.
Il concetto di congruenza
Secondo la definizione più diffusa e usata:
“Due figure che sovrapposte tramite traslazioni e/o rotazione, coincidono in ogni punto,
sono congruenti“.
Chiaro? Non tanto. Semplice? Nemmeno. Guardiamo le figure geometriche nella lavagna sotto e cerchiamo di chiarirci un po’ le idee.
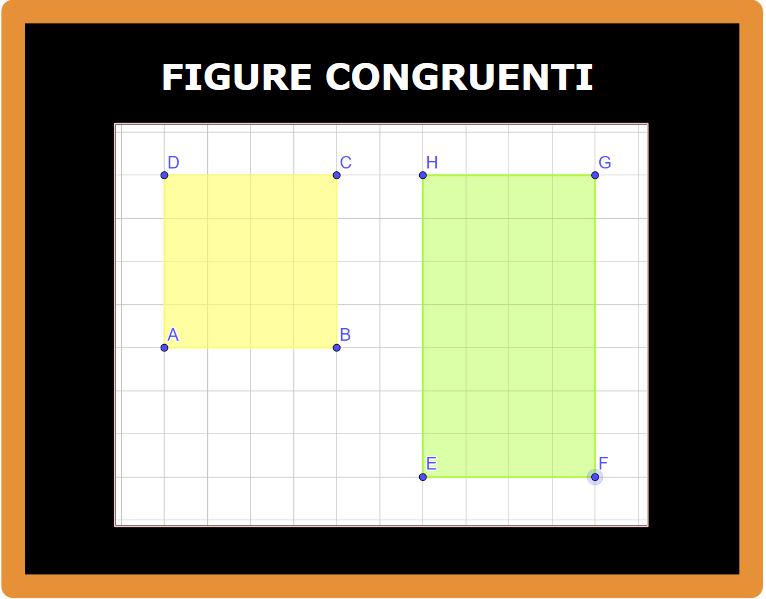
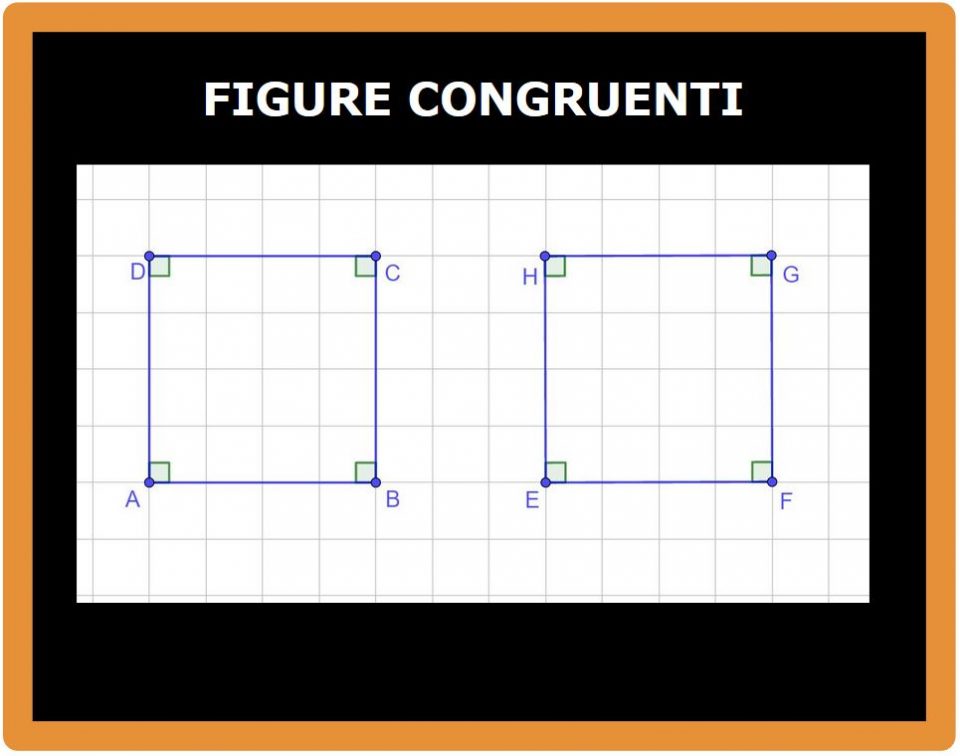
Abbiamo un quadrato ABCD e un rettangolo EFGH. Bene, adesso proviamo a spostare il quadrato sul rettangolo (questo spostamento è chiamato traslazione) e vediamo se tutti i punti del quadrato coincidono con quelli del rettangolo.
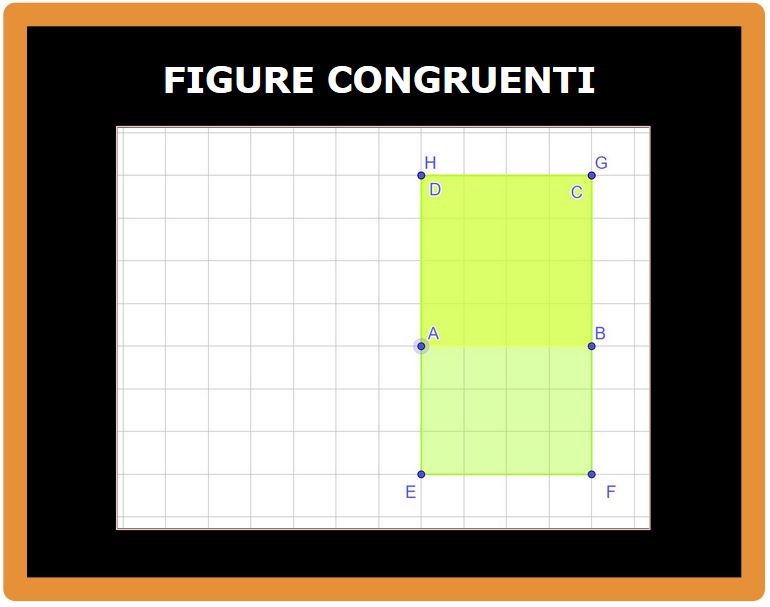
I vertici in alto, cioè i punti D e H coincidono così come coincidono i punti C e G. Ma gli altri vertici no.
Per esempio il vertica A e il vertice E non coincidono. Il lato AB e il lato EF non si sovrappongono. Si dice che le due figure non sono perfettamente sovrapponibili, quindi non sono congruenti. (Si vedeva anche a occhio che non erano perfettamente sovrapponibili).
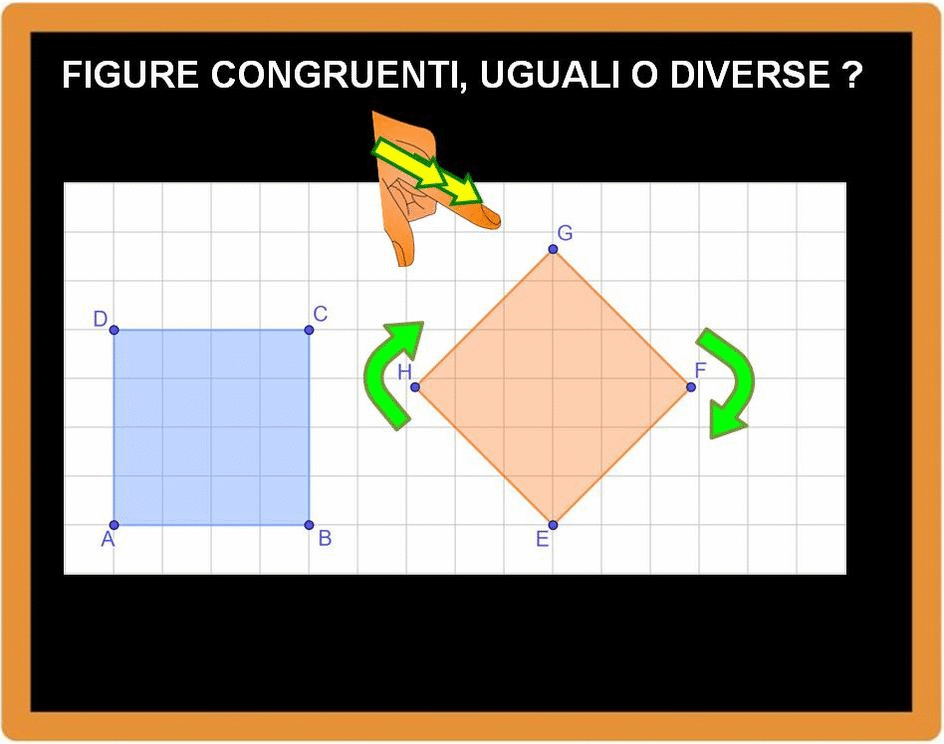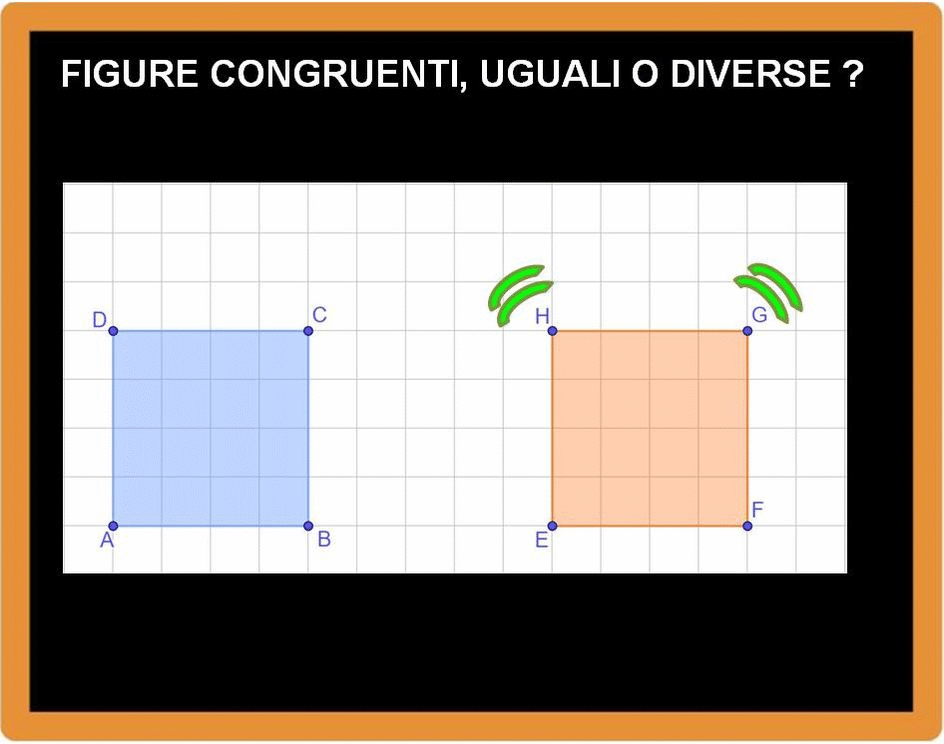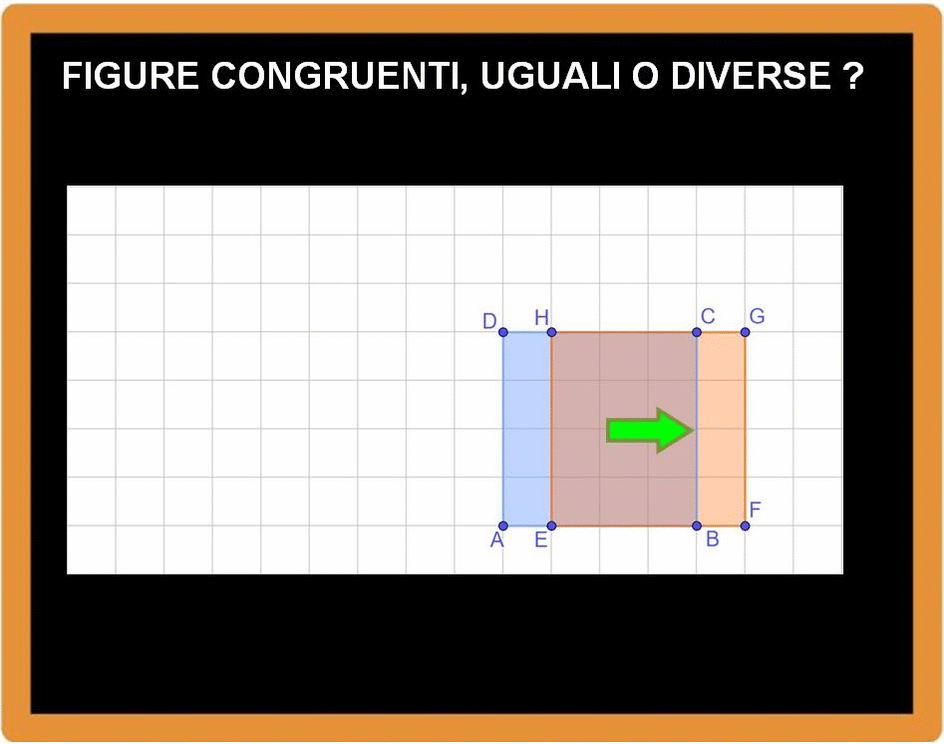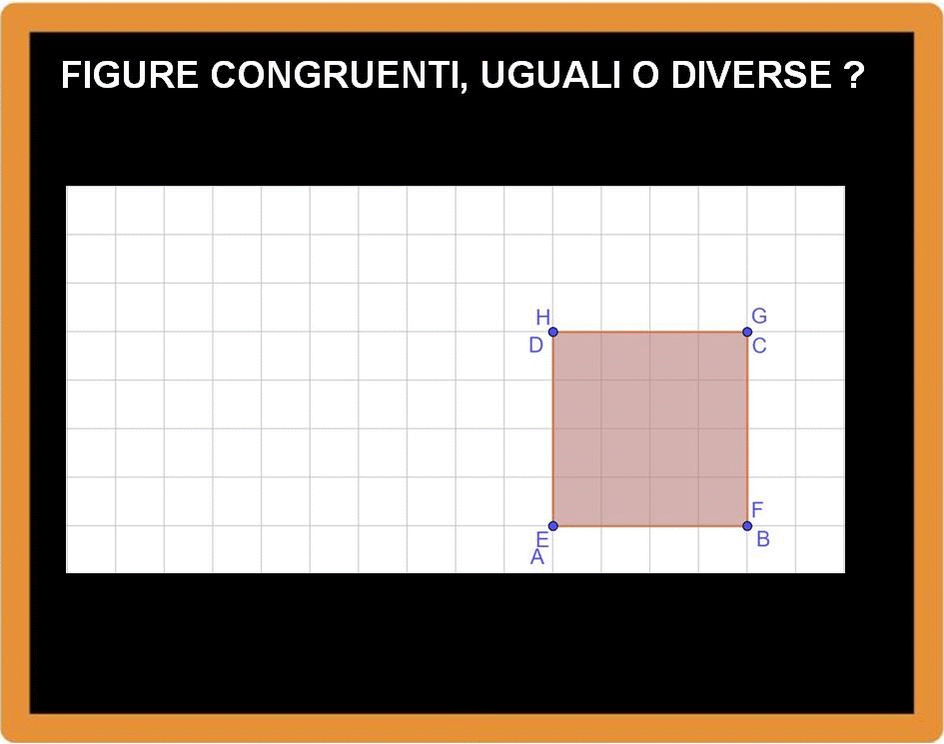
Osserviamo adesso queste altre due figure. Sono due quadrati, non farti ingannare dalla disposizione del secondo quadrato. (Un quadrilatero per essere un quadrato deve avere 4 angoli retti e tutti i 4 lati della stessa lunghezza).
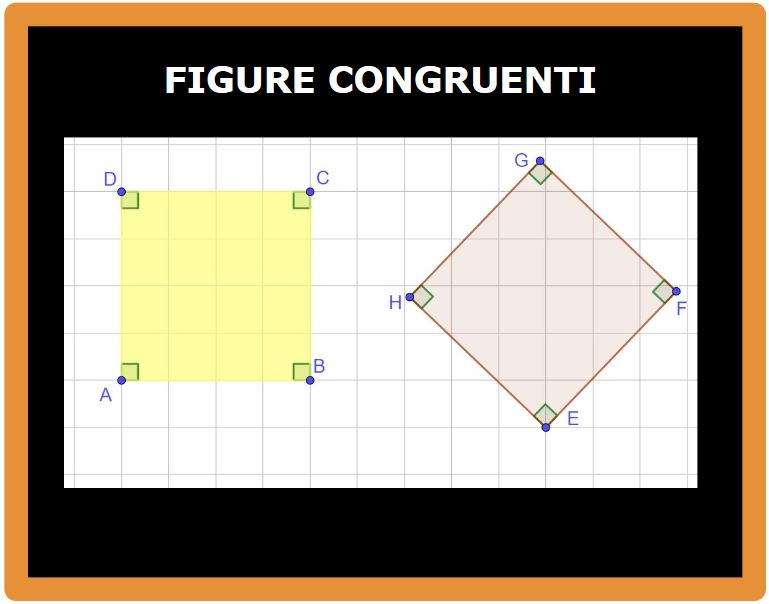
Bene, adesso dobbiamo verificare se sono sovrapponibili. Ruotiamo il secondo quadrato. Dobbiamo immaginare di dare una piccola spinta al vertice G e fare cadere il quadrato sul lato EF.
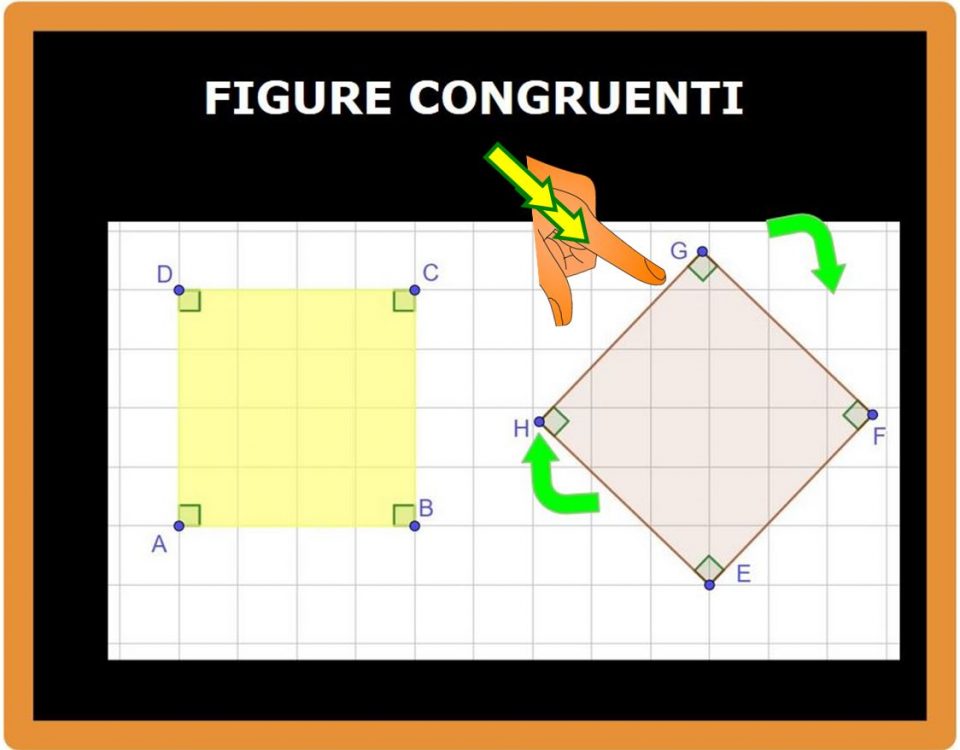
Dopo la rotazione, la situazione è questa:
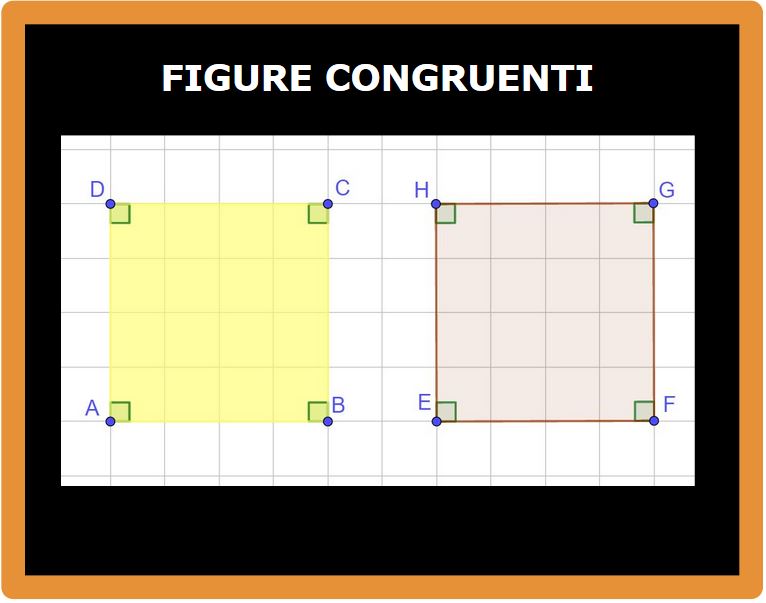
Adesso spostiamo (trasliamo) il primo quadrato sul secondo.
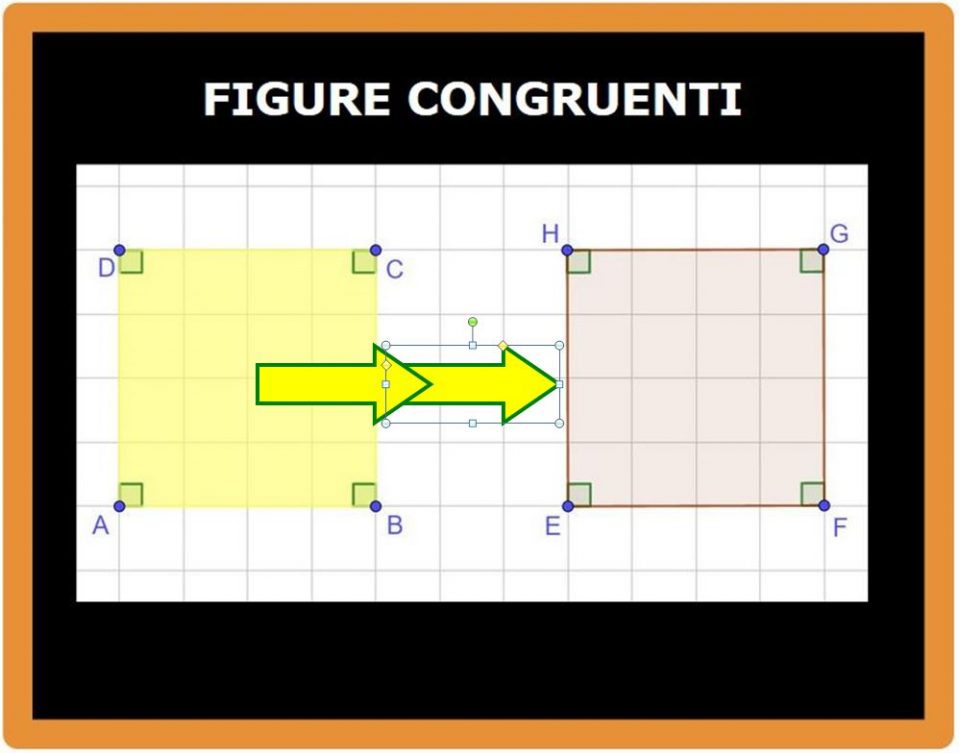
Dopo la traslazione, la situazione è quella che vedi sotto.
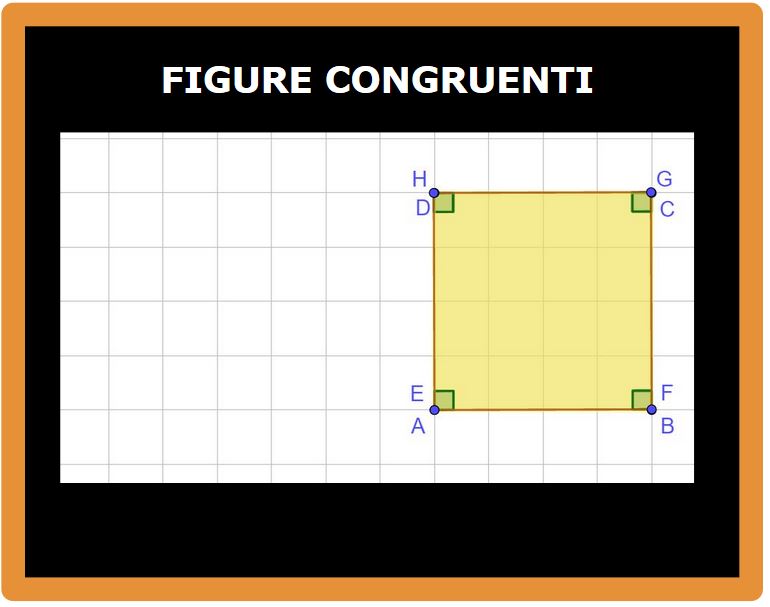
Le due figure si sovrappongono perfettamente. Non è più possibile distinguere la prima figura dalla seconda. I due quadrati sono congruenti.
Bene, questo è il concetto di congruenza.
Uguali o congruenti ?
Ma torniamo ai due quadrati dopo che abbiamo fatto ruotare il secondo. Sono uguali o diversi?
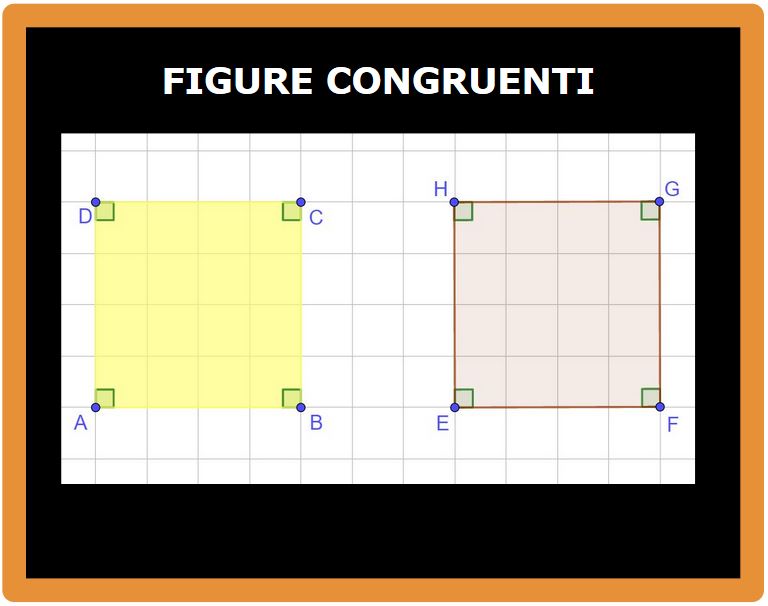
Qualcuno potrebbe dire che sono diversi perchè sono di colore diverso. Ma in geometria i colori non hanno nessun valore. Per cui togliamo il colore e vediamo cosa rimane.
Osserviamo ora i due quadrati. Come ti sembrano? La risposta che viene naturale è: “Uguali”. Per me (e non solo per me) andrebbe bene. Altri prof, invece, vogliono sentirsi dire che i due quadrati sono congruenti. In parole povere dire “le due figure sono congruenti” è un modo difficile per dire “le due figure sono uguali”.
Concludendo, se qualcuno mi chiede: “Che differenza c’è tra uguale e congruente?” Io rispondo: “Non c’è nessuna differenza”. Io ritengo che dire uguali o dire congruenti sia la stessa cosa, ma attenzione, ripeto, alcuni prof ci tengono molto alle definizioni. Per quanto mi riguarda, ai miei alunni faccio usare il termine congruente o il termine uguale a loro piacimento, perchè sono convinto che siano la stessa cosa. Ma non tutti la pensiamo allo stesso modo. Il consiglio che posso darti è di usare la terminologia che usano i tuoi insegnanti.
Il simbolo ≅ di congruenza geometrica
Passiamo alla questione simboli. Il simbolo dell’uguaglianza lo conosciamo tutti:
=
Esiste un simbolo che indica la congruenza? Ricordiamo che il concetto di congruente è esclusivo della geometria. Quindi ci potremmo chiedere:” Esiste un simbolo che indica la congruenza geometrica?” La risposta è “dipende”. Dipende dalla tua prof e dal libro che usate.
Infatti alcuni libri e alcuni prof per indicare la congruenza geometrica usano questo simbolo:
≅
cioè il segno di uguale con una piccola onda sopra.
Il simbolo ≅ di approssimazione
Ma attenzione. Lo stesso simbolo usato in aritmetica ha un significato molto diverso, infatti
≅
significa approssimativamente uguale a. Per esempio:
5,7 ≅ 6
Anche i simboli ∼ e ≈ indicano a approssimazione in aritmetica. Per cui bisogna fare attenzione.
Dato che ritengo congruente e uguale la stessa cosa, io non uso il simbolo ≅, ma uso solo il simbolo =.
Per indicare l’approssimazione matematica è possibile usare ≈.
Credo che l’importante sia evitare di generare confusione con simboli che possono essere intesi in più di un modo.
Esempio
L’immagine animata ci aiuta a capire che differenza c’è tra uguale e congruente.
Le due figure sono perfettamente sovrapponibili, allora si può dire che sono congruenti. Detto in modo semplice: le due figure sono uguali.
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai scaricare liberamente le tavole numeriche.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori.