Prodotti notevoli: il quadrato di un binomio

Questa propria non l’hai capita. Oggi in classe seguivi, eri attento, ma niente da fare. La prof spiegava e tu non la capivi. Sin dal principio, dal nome. Perché si chiamano notevoli? Non ti preoccupare, con 10 minuti di impegno riuscirai a capire come si eseguono i prodotti notevoli e in particolare il quadrato di un binomio. Però è meglio essere chiari. L’unico modo per imparare a sviluppare in modo corretto il quadrato di un binomio è allenarsi, come in palestra, in piscina o a calcetto. Leggendo questa pagina capirai perchè si chiamano prodotti notevoli e capirai anche il procedimento che porta al risultato corretto. Ma se non ti eserciterai, sarà tempo perso. (Andare in palestra solo un giorno è come non andarci mai, non si ottiene nessun risultato.) Chiarito questo, rimbocchiamoci le maniche e cominciamo subito.

Indice

Perché si chiamano prodotti notevoli
Esempio 1
Esempi di monomi
Esempi di binomi
Quadrato di un binomio
Riconoscere i quadrati di binomio
Calcolo del quadrato di un binomio: procedimento completo
Calcolo del quadrato di un binomio: usando la regolaq
Esempio 2

Iscriviti al mio canale Youtube

Perché si chiamano prodotti notevoli

Cominciamo dal loro nome e analizziamo le parole che lo compongono:

Prodotti: il prodotto è l’operazione di moltiplicazione. E fin qua non c’è nulla di difficile. Sappiamo quindi che si tratta di eseguire una o più moltiplicazioni.
Notevoli: l’unica cosa che hanno di notevole questi prodotti è la loro frequenza. Mi spiego meglio. Si tratta di moltiplicazioni che capita spesso di incontrare. Quando li incontri, è meglio riconoscerli. Infatti riconoscere un prodotto notevole ti permette di risparmiare tempo ed errori applicando una semplice formuletta, che va ricordata. È necessaria un po’ di memoria, ma non è un dramma. Se ricordi la formula dell’area del triangolo puoi anche ricordare la formula di un prodotto notevole.

Esempio 1

Il prodotto notevole che andiamo a eseguire è il quadrato di un binomio. Come dici? Non ti ricordi cos’è un binomio? Allora è meglio ripassare un po’ prima di cominciare con l’esercizio vero e proprio.

Un binomio è la somma algebrica (quindi ci può essere sia il segno più “+” sia il segno meno “-“) di due monomi. Come? Non ti ricordi neanche cosa si intende per monomio? Ripassiamolo. Se ti accontenti di una spiegazione velocissima: i monomi sono il risultato della moltiplicazione tra lettere e numeri, oppure tra sole lettere oppure un monomio può essere formato solo da un numero.

Esempi di monomi

Esempi di monomi possono essere:

2a, prodotto tra il numero 2 e la lettera a;
ab, prodotto tra le lettere a e b;
5, monomio con la parte letterale assente;
3ab, prodotto tra il numero 3, la lettera a e la letterea b;
b²c, prodotto tra il quadrato della lettera b e la lettera c.

Ti ricordo che nel monomio 2a, tra il numero 2 e la lettera a è sottinteso il segno della moltiplicazione • . Quindi:

2a = 2 · a

Lo stesso discorso vale per tutti gli altri monomi, ad esempio:

3ab = 3 · a · b

Il segno della moltiplicazione non si scrive perchè altrimenti tutti i calcoli sarebbero molto più lunghi da scrivere e sarebbe più facile confondersi e sbagliare.

Se vuoi qualche informazione più accurata potresti dare un’occhiata a questo mio articolo, in cui spiego proprio cosa sono i monomi.

Esempi di binomi

Vediamo adesso molto velocemente qualche esempio di binomi (che ti ricordo essere la somma albebrica tra due monomi):

a + b;
2a + 3b;
7 + c;
5ab + 7a,
6b – 5c;
b²c + 2b.

Quadrato di un binomio

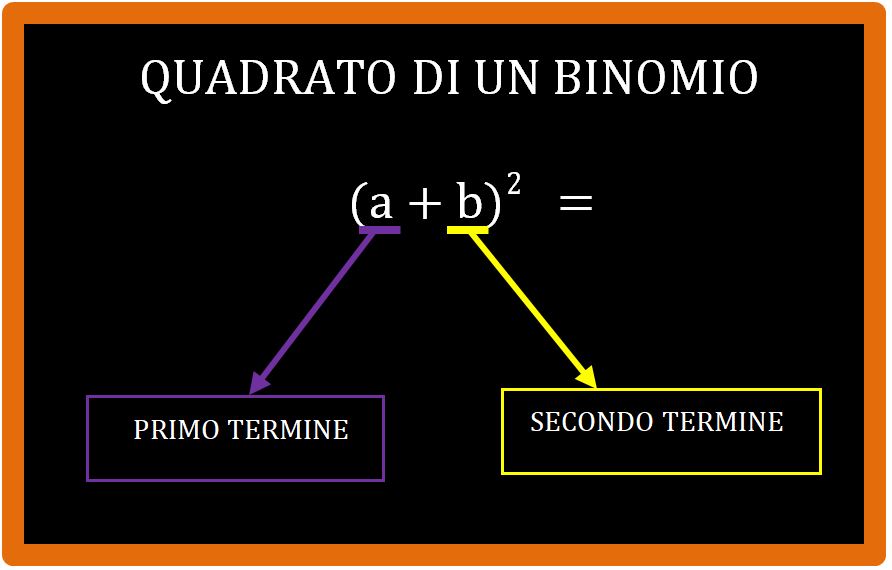
Vediamo il primo esempio di prodotti notevoli: il quadrato di un binomio. Adesso che abbiamo capito cosa è un binomio, è arrivato il momento di elevarlo al quadrato, cioè alla seconda. Quindi prendiamo in considerazione il binomio a + b e lo eleviamo tutto al quadrato. Vediamo come si scrive:

Per scrivere in modo corretto il quadrato di un binomio si devono usare le parentesi. Infatti, proviamo a osservare con attenzione l’espressione numero 1:

a + b²

In questo caso l’esponente 2 si riferisce solo alla lettera b, invece noi vogliamo che tutto il binomio sia elevato al quadrato. Per ottenere questo dobbiamo usare le parentesi:

(a + b)²

che è il modo corretto di scrivere il quadrato di un binomio. È arrivato il momento di capire come si esegue.

Riconoscere i quadrati di binomio

Per essere sicuri di avere capito i prodotti notevoli: il quadrato di un binomio, eseguiamo un esercizio. Dobbiamo riconoscere quindi i binomi (deve essere la somma o la sottrazione tra due termini) elevati alla seconda.

Nell’immagine si vedono vari polinomi. Solo alcuni sono quadrati di binomio. Prova a individuarli e a sottolinearli. Trovi la soluzione alla fine dell’articolo.

Calcolo del quadrato di un binomio: procedimento completo

Prima vediamo tutto il procedimento, vediamo a quale risultato ci porta e poi eneunciamo la formula che dovremo ricordare a memoria. So che ricordare le cose a memoria a molti sembr antipatico, ma in questo caso ricordare una formula ci permetterà di evitare tutti i calcoli che ora andremo a fare. Giudicherai tu stesso se è conveniente oppure no.

Ricordiamoci il significato delle potenze, scrivere tre al quadrato è la stessa cosa di scrivere una moltiplicazione in cui il tre è ripetuto due volte. Con i numeri si scrive così:

3² = 3 · 3

Bene. La stessa cosa vale per un binomio. Elevare un binonio al quadrato è la stessa cosa di scrivere una moltiplicazione in cui il binomio è ripetuto due volte. Vediamo:

Adesso dobbiamo moltiplicare i due binomi. Procediamo passo passo per essere sicuri di fare bene. Spiegarlo con le parole è più difficle che fare i calcoli con i numeri. Per moltiplicare tra loro due binomi, il primo termine del primo binomio va moltiplicato per ogni termine del secondo binomio. E poi il secondo termine del primo binomio va moltiplicato per ogni termine del secondo binomio. Complicato? Sembrerebbe di si, ma andiamo a applicare quanto detto sui numeri.

La prima moltiplicazione che dobbiamo eseguire è a · a. Ricordiamoci di fare attenzione ai segni. Il risultato che otteniamo è a².

Adesso moltiplichiamo il primo termine del primo binomio, cioè a, per il secondo termine del secondo binomio, cioè +b.

Otteniamo come risultato +ab. Ti ricordo di fare sempre attenzione ai segni.

Benissimo, ma non abbiamo ancora finito, perchè dobbiamo ripetere lo stesso procedimento per il secondo termine del primo monomio.

Sarai d’accordo con me che il procedimento, anche se non è poi così difficile, però è molto lungo ed è facile sbagliare. Con la formula da ricordare a memoria, tutti questi passaggi non saranno necessari.

Facendo sempre attenzione ai segni otteniamo +ab.

Ci manca l’ultima moltiplicazione, cioè moltiplicare il secondo termine del primo binomio per il secondo termine del secondo binomio, cioè b • b.

Il risultato dell’ultima moltiplicazione è b².

Fantastico, siamo quasi alla fine. Adesso dobbiamo sommare tra loro i monomi simili. Ti ricordo che i monomi simili sono quelli che hanno la stessa parte letterale. Vado a sottolineare i monomi simili.

Bene, il risultato della somma è 2ab.

Ok, abbiamo finito. Dopo quattro moltiplicazioni e una somma siamo arrivati al risultato finale. Questo procedimento è sicuramente corretto, ma è lungo e poco praticabile.

Calcolo del quadrato di un binomio: usando la regola

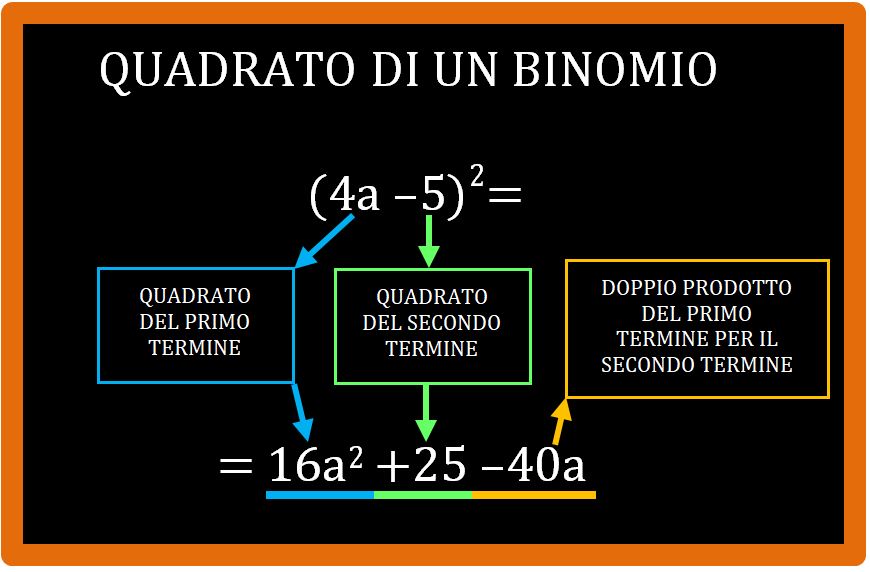
La scorciatoia per arrivare direttamente al risultato finale è ricordare questa regola:

Il quadrato di un binomio è uguale al:

quadrato del primo termine,
più il quadrato del secondo termine,
più (oppure meno) il doppio prodotto del primo termine per il secondo termine.

Forse la scorciatoia ti sembra complicata quanto il procedimento completo, ma ragioniamoci su.

Partiamo sempre dallo stesso binomio di prima:

Mettiamoci d’accordo sui nomi. Il primo termine, cioè il primo componente, del binomio è a. Il secondo termine (componente) del binomio è b.

Per risolvere in modo veloce questo prodotto notevole (senza eseguire tutte le moltiplicazioni che abbiamo visto nel procedimento precedente) dobbiamo effettuare 3 passaggi.

Dobbiamo scrivere:

Il quadrato del primo termine. Abbiamo appena visto che il primo termin è a, quindi a elevato alla seconda fa a².

Fantastico. Adesso passiamo al secondo passaggio. Il quadrato del secondo termine.

2. Il secondo termine è b. Quindi b elevato alla seconda fa b².

Benissimo, siamo già quasi alla fine. Fino a ora abbiamo scritto il quadrato del primo termine e il quadrato del secondo termine. Ci manca solo un ultimo passaggio.

3. Dobbiamo moltiplicare il primo termine per il secondo termine, cioè dobbiamo fare a • (+b), che fa +ab

a · (+b) = +ab

e poi moltiplicare questo risultato che abbiamo ottenuto per 2 (la regola infatti dice doppio prodotto, che vuol dire prima moltiplicare i termini tra loro e poi ottenere il doppio, cioè moltiplicare per due).

2 · (+ab) = +2ab

Abbiamo finito. Esercizio concluso e risultato corretto. Adesso sai come si calcola il più comune dei prodotti notevoli: il quadrato di un binomio.

Esempio 2

Facciamo un altro esempio per essere sicuri di avere capito i prodotti notevoli: il quadrato di un binomio.

Calcoliamo il seguente prodotto notevole: (5 + a)²

Usiamo la formula. Il primo termine è 5, il secondo termine è a. Iniziamo scrivendo il quadrato del primo termine, cioè dobbiamo fare 5 elevato alla seconda:

5 · 5 = 25

Benissimo. Adesso scriviamo il quadrato del secondo termine. Il secondo termine è a, quindi a elevato alla seconda fa:

a · a = a²

Perfetto. Siamo quasi alla fine. Ci manca l’ultimo passaggio. Dobbiamo moltiplicare i due termini tra loro e poi moltiplicarli per due:

5 · (+a) = +5a

Mi raccomando: in questo passaggio bisogna fare molta attenzione ai segni.

+5a · 2 = +10a

Detto in modo complicato: abbiamo calcolato il doppio prodotto del primo termine per il secondo. Invece usando un modo più semplice: abbiamo moltiplicato il primo termine per il secondo (facendo attenzione ai segni) e poi abbiamo moltipliato il risultato che abbiamo ottenuto per due.