Dopo avere visto chi ha inventato il calcolo letterale è arrivato il momento di entrare nel mondo dell’algebra. Cominciamo cercando di capire cosa sono i monomi. Faremo prima una breve introduzione sul calcolo letterale e ti accorgerai che in realtà lo hai già utilizzato, anche se non lo sapevi.
Come dice il nome stesso, il calcolo letterale prevede la presenza non solo dei numeri, ma anche delle lettere dell’alfabeto. Ma niente paura, le operazioni sono le stesse. Non perdiamo altro tempo e cominciamo a vedere cosa sono i monomi.
Indice
- Esempio di espressione letterale: l’area del triangolo
- I monomi
- Come si scrive un monomio
- Parte letterale e coefficiente numerico
- Monomi senza coefficiente numerico
- Monomi senza parte letterale
- Esercizi
- Risultati
Esempio di espressione letterale: l’area del triangolo
In seconda media (e forse anche alle elementari) hai studiato come si calcola l’area del triangolo. È una formula breve che va imparata a memoria (esiste una dimostrazione, ma per noi è sufficiente ricordare la formula).
Area del triangolo = (base · altezza) : 2 . Che usando numeri e lettere si scrive così:
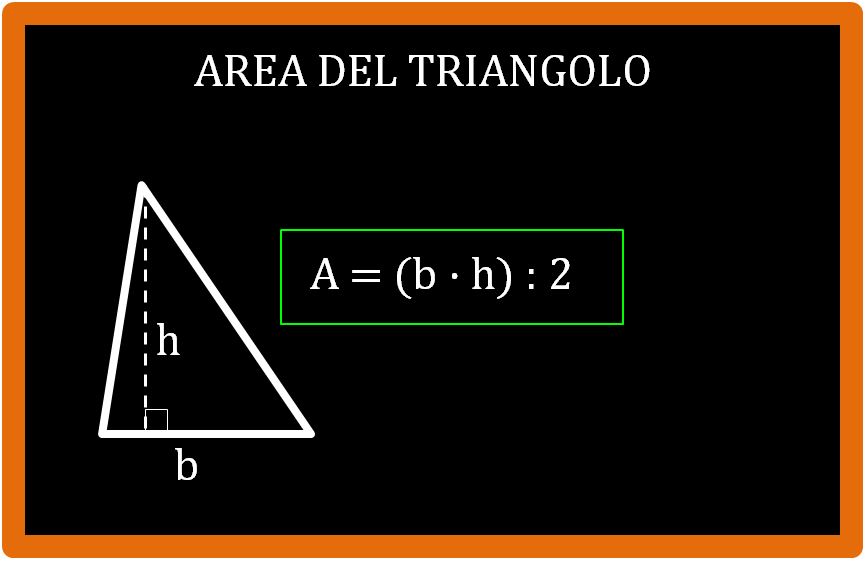
Come vedi, nella formula dell’area del triangolo hai già usato numeri e lettere. Per cui in realtà niente di nuovo. Senza saperlo hai scritto un’ espressione letterale. Possiamo dare una prima definizione:
“Un’ espressione letterale è una scrittura in cui sono presenti numeri, lettere e segni.”
I monomi
Sui monomi le cose da dire sono tante. Non sono difficili, ma sarebbe opportuno ricordarle tutte. Iniziamo con calma un passo alla volta.
I monomi sono un esempio di espressione letterale. Facciamo qualche esempio per capirci. Guarda le immagini sotto.

Siamo tutti d’accordo se diciamo che quella che vedi alla lavagna è una Ferrari. Una Ferrari è un tipo di macchina. Oppure ancora:

Adesso alla lavagna hai appena osservato un gatto. Un gatto è un tipo di animale.
Perfetto, (b · h) : 2 è un monomio. Un monomio è un tipo di espressione letterale.

È arrivato il momento di cercare di capire cosa sono i monomi e di dare una definizione di monimio.
Un monomio è un prodotto tra lettere e numeri oppure un prodotto di sole lettere oppure ancora un monomio può essere formato solo da un numero.
Detto in altre parole: un monomio è una moltiplicazione tra lettere e numeri oppure una moltiplicazione tra sole lettere. Facciamo subito alcuni esempi:
2 · a; 35 · a · b; 7; a · b · c; x · y; 4; sono esempi di monomi.
Anche 4 è un monomio, infatti può essere immaginato come 4· x° (si legge quattro per ics elevato alla zero). Siccome qualsiasi quantità elevato zero, dà come risultato 1, allora:
4 · x° = 4 · 1 = 4
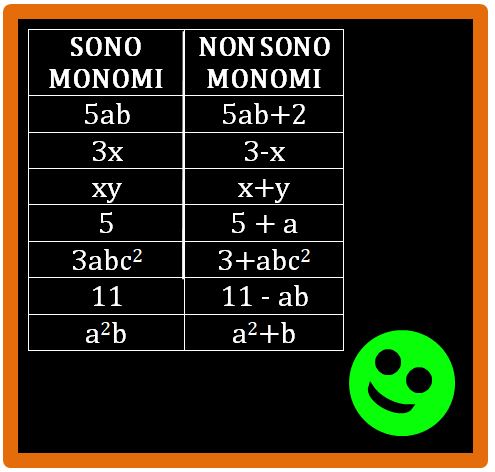
Osserva la tabella. Nella colonna di destra abbiamo diversi monomi. Nella colonna di sinistra puoi leggere altre espressioni letterali che però non sono monomi. E non sono monomi perché oltre alla moltiplicazione, c’è anche l’addizione o la sottrazione. Quindi per parlare di monomio ci deve essere solo la moltiplicazione tra numeri e lettere oppure solo la moltiplicazione tra lettere e lettere.
Come si scrive un monomio
In tutti i libri i monomi sono sempre scritti rispettando alcune regole. Anche la tua prof scriverà i monomi in questo modo: si usano sempre lettere minuscole e si scrivono prima i numeri. Queste regole servono per scrivere in modo ordinato. Da un punto di vista matematico scrivere
2·a oppure a·2
è la stessa cosa (proprietà commutativa della moltiplicazione). Ma viene utilizzato sempre il primo modo. Questa uniformità di scrittura permette di essere ordinati. E ti accorgerai che l’ordine è molto importante quando avrai a che fare con le operazioni con i monomi. La matematica e l’anarchia non vanno d’accordo.
Parte letterale e coefficiente numerico
In alcuni monomi è possibile identificare una parte letterale e una parte numerica. La parte numerica è chiamata con un nome un po’ più difficile: coefficiente numerico o semplicemente coefficiente. Come dice già il nome, la parte letterale è quella composta dalle lettere, invece la parte numerica è quella composta dai numeri. Devi ammettere che questo è facile. Vediamo qualche esempio.
Nel monomio 2·a (si legge due per a) il coefficiente numerico è 2, invece la parte letterale è a. Possono sembrarti cose banali, ma man mano che andremo avanti tutte queste definizioni saranno molto utili, quindi non sottovalutiamole.
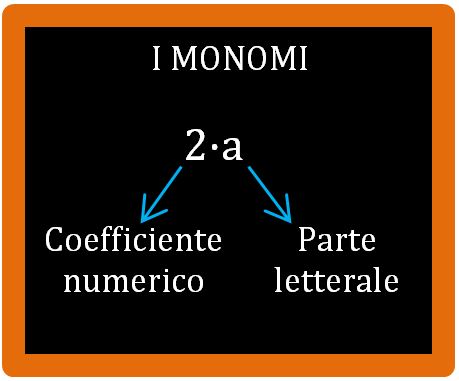
Quasi sempre, il segno • della moltiplicazione non viene scritto. Per cui:

La parte letterale può essere composta o dalle prime lettere dell’alfabeto: a, b, c, ecc, oppure può essere composta da altre lettere come x, y, z, ecc. Non cambia nulla, una lettera vale un’altra. Si potrebbero usare anche le lettere q, w, e, r, t, y, ecc. Ma la tua prof userà o le prime lettere dell’alfabeto oppure x e y.
Monomi senza coefficiente numerico
Alcuni monomi possono essere composti solo da lettere. Per esempio: ab, b2, a2c, ecc sono tutti esempi di monomi in cui compaiono solo lettere. In questo caso il coefficiente numerico è 1. Mi spiego meglio. Se ti chiedo di scrivere un monomio in cui il coefficiente è 1 e la parte letterale è ab, tu scrivi così:
1ab
È corretto, ma ragioniamo. Sappiamo che tra il numero 1 e le lettere ab, c’è il segno di moltiplicazione, cioè
1 · ab
Come ricorderai dalle scuole elementari, il numero 1 è l’elemento neutro della moltiplicazione (infatti 2 x 1 = 1, oppure 5 x 1 = 5). Per cui
1 · ab = ab
Ricordiamoci quindi che, in tutti quei monomi in cui non si vede il coefficiente numerico, in realtà il coefficiente c’è ed è 1.
Monomi senza parte letterale
Esistono anche monomi che sono formati solo dal coefficiente numerico e non hanno nessuna parte letterale.
In altre parole, un numero come ad esempio 13 può essere considerato un monomio.
Con lo stesso ragionamento, qualsiasi numero può essere considerato un monomio in cui la parte letterale è assente. Se ti chiedo di scrivere un monomio che ha per coefficiente numerico 8 e nessuna parte letterale, tu dovrai scrivere semplicemente 8.
(C’è da dire che non tutti i libri di matematica sono d’accordo su questo, infatti alcuni libri non considerano la possibilità di avere monomi senza la parte letterale. Come sempre ti consiglio di seguire la strada che ti indica la tua prof. Io credo che sia corretto avere monomi senza parte letterale).
Esercizi
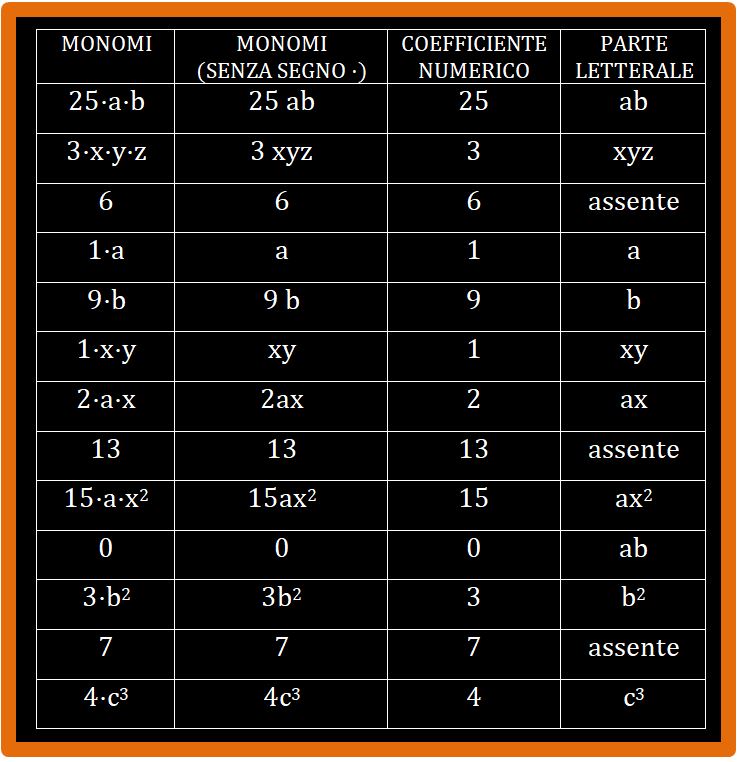
Nella tabella sotto puoi leggere alcuni monomi scritti sia con il segno · della moltiplicazione sia senza segno. Da ora in poi, io li scriverò senza segno, perchè il linguaggio della matematica deve essere sintetico e veloce. Questo segno si può evitare. Quindi sia chiaro da ora in poi se leggi
7a sai che vuol dire 7·a
Le prime tre righe della tabella sono complete. Adesso possiedi tutte le conoscenze e gli strumenti per completare la tabella. Armati di carta e penna e buona volontà. Non ti preoccupare se sbagli. Sbagliare è normale. Nessuno verrà a rimproverarti. Trovi i risultati alla fine della pagina.
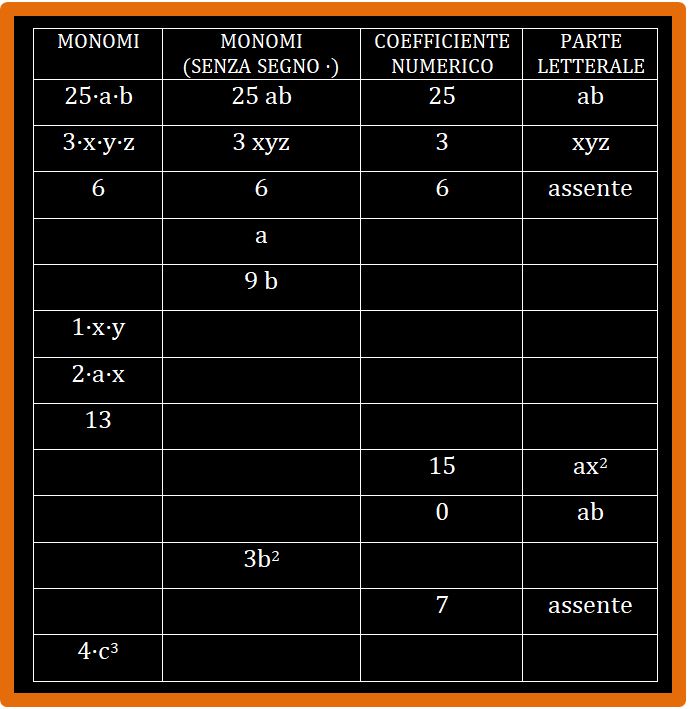
Per il momento direi che ci possiamo fermare qui. Non voglio mettere troppa carne al fuoco. Nell’articolo successivo parlerò di grado di un monomio, monomi simili e addizione e sottrazione tra monomi. Buon lavoro.
A questo link della Casa Editrice Zanichelli puoi trovare e scaricare come file pdf le tavole numeriche.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it; sarò grati ai lettori che segnaleranno eventuali errori.
Risultati