Oggi la prof di matematica ha spiegato come si calcola il grado di un monomio. Ha detto che esistono monomi di primo, secondo e terzo grado. Tu pensavi alla bici nuova del tuo compagno di banco e non eri molto attento. Ora sei a casa con gli esercizi da svolgere e non sai da che parte cominciare. Non ti preoccupare, con 5 minuti di impegno sarai in grado di calcolare il grado di qualsiasi monomio.
Indice
- Breve ripasso
- Parte letterale con una sola lettera – Esempio 1
- Esercizio 1
- Parte letterale con più lettere – Esempio 2
- Terzo esempio
- Altri esempi
- Esercizio 2
- Esercizio 3
- Risultati
Breve ripasso
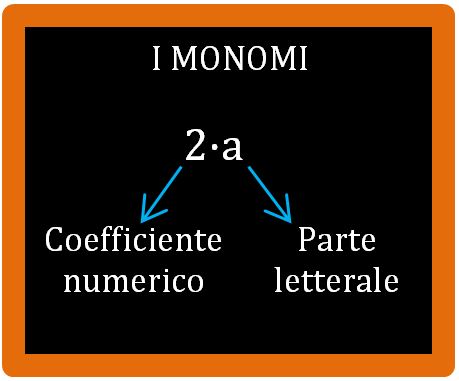
Prima di parlare di grado di un monomio dobbiamo sapere cosa è un monomio. Ripassiamo brevemente. Un monomio è un’operazione di moltiplicazione tra numeri e le lettere oppure tra lettere e lettere. Hai capito bene. Da ora in poi non lavoriamo più solo con i numeri, ma anche con le lettere (per questo motivo si chiama calcolo letterale). Come puoi leggere nella lavagna sotto, in un monomio è possibile distinguere una parte letterale e una parte numerica, chiamata coefficiente numerico. Se vuoi altre notizie sui monomi, puoi leggere questo mio articolo.
Esempio 1: parte letterale con una sola lettera
Dopo questo breve ripasso, vediamo subito qualche esempio che può aiutarci a capire come si calcola il grado di un monomio. Partiamo dai casi più semplici, cioè quei casi in cui la parte letterale del monomio è costituita da una sola lettera.Osserviamo la lavagna:

Il monomio 5a2 (si legge cinque a alla seconda) è un monomio di secondo grado perchè l’esponente della parte letterale è 2. (Ti ricordo che 5a2 = 5 · a2).
Facciamo un altro esempio:

Il monomio 7b3 (si legge sette b alla terza) è un monomio di terzo grado perchè l’esponente della parte letterale è 3. Fin qui non mi pare che ci sia nulla di difficile. Possiamo subito dire che per determinare il grado di un momonio dobbiamo guardare l’esponente della parte letterale.
Ancora un esempio:

Il monomio 43a2 (quattro alla terza a alla seconda) è un monomio di secondo grado perchè l’esponente della parte letterale è 2. Anche se il coefficiente numerico ha esponente 3, a noi non interessa. Per determinare il grado di un monomio si deve guardare soltanto l’esponente della parte letterale.
Continuiamo:

Il monomio 6a è un monomio di primo grado perchè l’esponente della parte letterale è 1. Infatti, se ti ricordi dalle potenze 31 = 3, questo perchè l’esponente 1 non si scrive.
Esercizio 1
Ora prova tu a stabilire il grado di questi monomi. Meglio se prendi carta e penna. Mettiti alla prova e non ti preoccupare se sbagli. Sbagliare è normale. E poi non c’è nessuno che ti guarda e nessuno lo verrà mai a sapere. Trovi i risultati alla fine della pagina. I risultati ti servono per capire se hai fatto bene.

Esempio 2: parte letterale con più lettere
Fino a ora abbiamo visto esempi in cui la parte letterale era costituita da una sola lettera. Vediamo adesso come si calcola il grado di un monomio in cui la parte letterale è costituita da più lettere. Facciamo prima un esempio con i numeri e poi enunciamo la regola.

Il monomio 2a2b3 (due a alla seconda b alla terza) è un monomio di quinto grado. Infatti, quando la parte letterale è costituita da più lettere, bisogna sommare gli esponenti di tutte le lettere.

Esempio 3
Facciamo un altro esempio per essere sicuri di avere capito come si calcola il grado di un monomio.
Determiniamo il grado del monomio 4a2b2. Anche in questo caso per determinare il grado del monomio bisogna addizionare gli esponenti della parte letterale.

È un monomio di quarto grado infatti:

Facciamo ancora un esempio. Determiniamo il grado del monomio 9ab2 (nove a b alla seconda). Ti ricordo ancora una volta che per determinare il grado di qualsiasi monomio dobbiamo andare a sommare gli esponenti della parte letterale.

Il monomio 9ab2 è un monomio di terzo grado. Vediamo perchè.

So cosa stai pensando. Stai pensando che nella lettera a non compare nessun esponente. Ma come abbiamo imparato quando abbiamo studiato le potenze:
3 = 31.
E questo ragionamento vale anche per le lettere:
a = a1.
Altri esempi
Facciamo ancora altri esempi:

Sommiamo gli esponenti della parte letterale e vediamo cosa otteniamo:
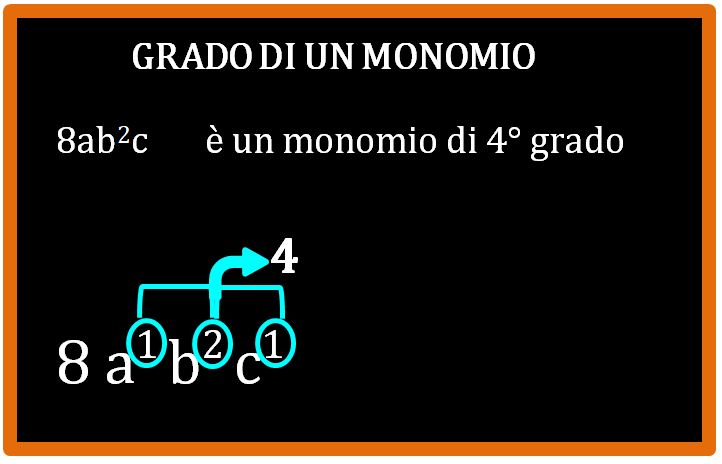
Il monomio 8ab2c è un monomio di quarto grado.
Esercizio 2
È arrivato il momento di provare da solo. Ti suggerisco di prendere carta e penna e di eseguire l’esercizio su un foglio. Somma gli esponenti della parte letterale e avrai determinato in modo corretto il grado dei monomi. Non ti preoccupare se sbagli. Sbagliando si impara. Trovi i risultati alla fine della pagina. Buon lavoro.

Terzo esercizio
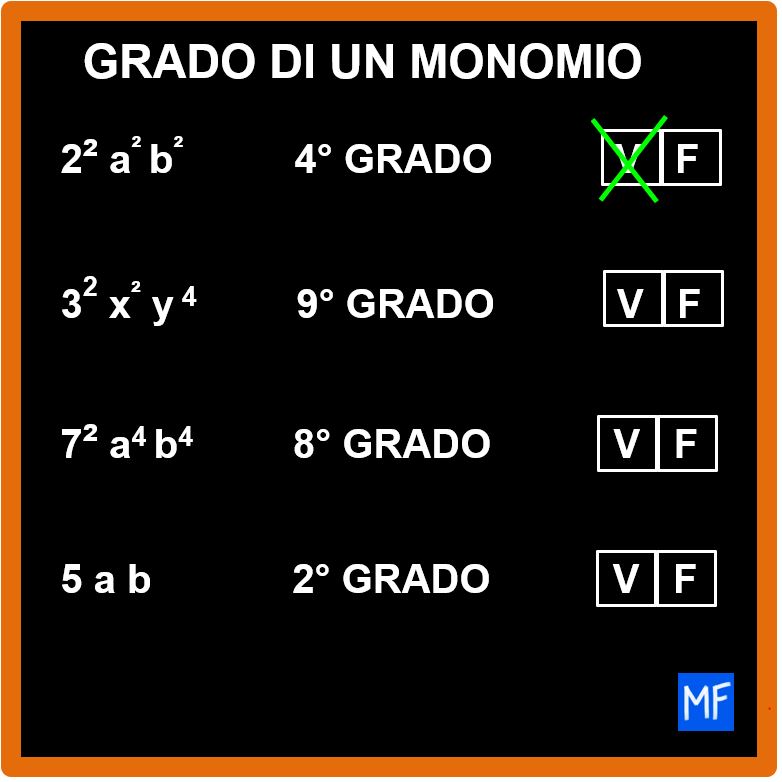
Vediamo ancora un altro esercizio.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it; sarò grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
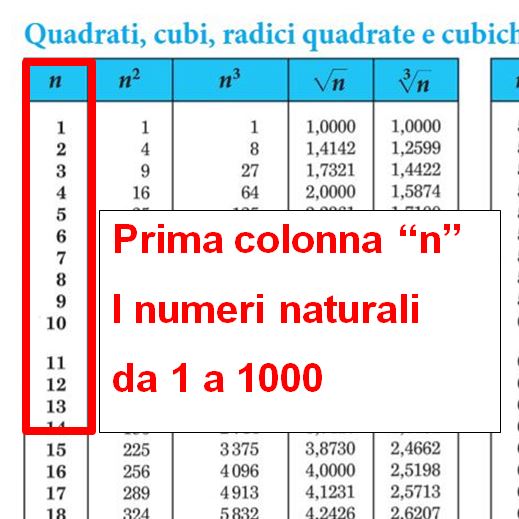
A questo link della Casa Editrice Zanichelli puoi trovare e scaricare liberamente le tavole numeriche.
Risultati esercizio 1

Risultati esercizio 2

Risultati esercizio 3
Vero – falso, perchè è di sesto grado – vero – vero