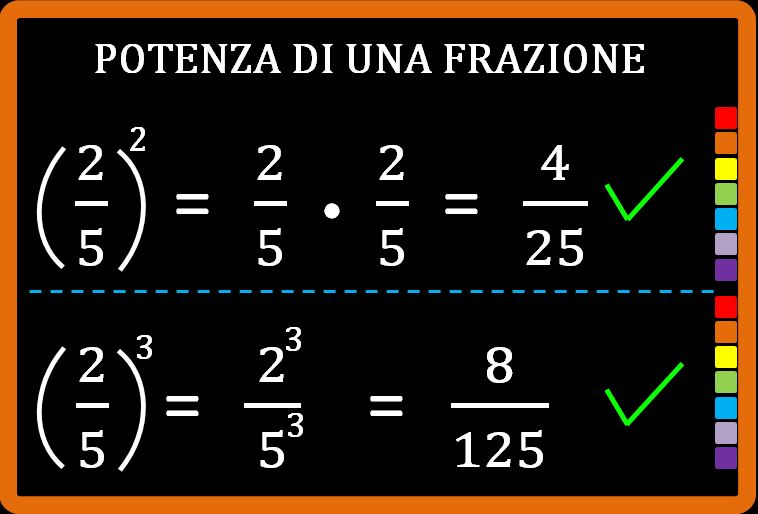
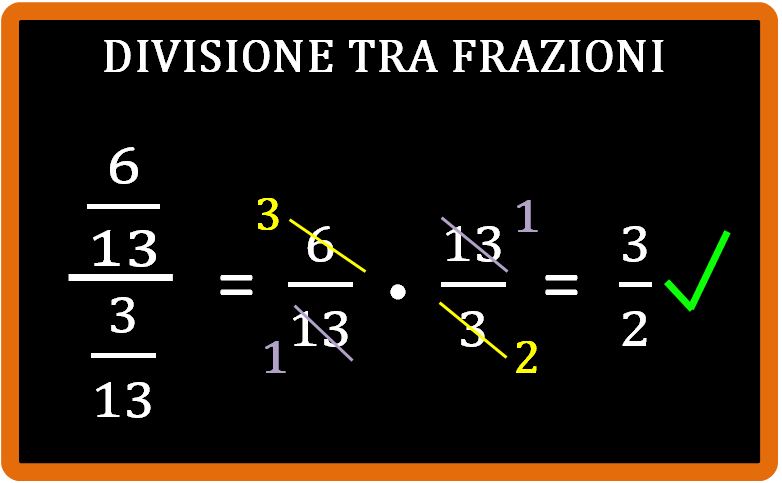
Cara mamma, oggi tuo figlio ti ha chiesto di aiutarlo con un argomento che prorpio non riesce a capire: la semplificazione in croce delle frazioni. Tu non ricordi tanto bene di cosa si tratta e in verità non ti piace neanche il nome di questo argomento. Ma niente paura. Se vuoi, puoi leggere questo mio articolo in cui spiego la semplificazione in croce. Oggi vedremo un altro esempio di semplificazione in croce che ci aiuterà a capire meglio di cosa si tratta.
Indice
- Esercizio
- Procedimento sconsigliato (ma possibile)
- Procedimento consigliato
- Esercizi svolti su Youtube
Esercizio
Cominciamo con un esempio numerico. Dobbiamo eseguire la moltiplicazione tra frazioni che leggi alla lavanga sotto: cinque diciottesimi per nove decimi.
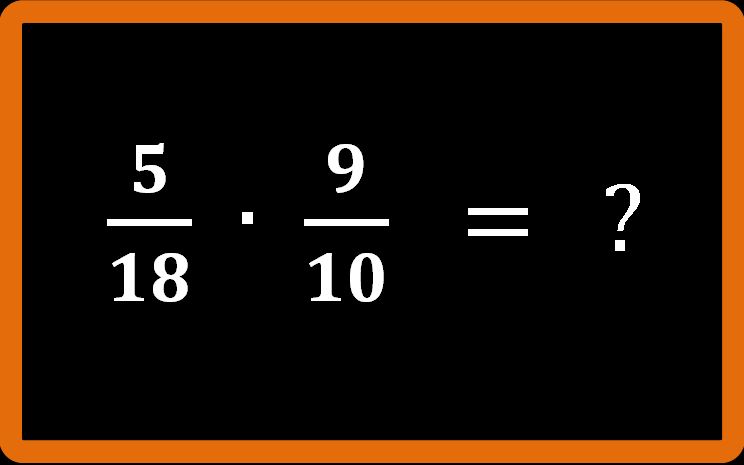
Procedimento sconsigliato
scAd alcuni non piace semplificare in croce e seguono un procedimento diverso, cioè moltiplicano il numeratore della prima frazione per il numeratore della seconda e il denominatore della prima frazione per il denominatore della seconda. In questo modo:

Il procedimento, dal punto di vista matematico, è corretto, ma ci sono almeno un paio di motivi che lo rendono sconsigliabile. Il primo motivo è che facendo in questo modo otteniamo come risultato la frazione 45 su 180 che ha al denominatore un numero relativamente grande. E a noi non piace maneggiare numeri grandi. In realtà non piace a nessuno. Nei laboratori del CERN a Ginevra o in quelli della NASA a Washington la pensano allo stesso modo. Là usano la notazione esponenziale proprio per evitare di lavorare con numeri grandi.
Dopo avere ottenuto questo risultato non abbiamo finito perchè bisogna ridurre ai minimi termini. Avendo a che fare con numeri grandi, la riduzione ai minimi termini diventa un processo laborioso, lungo in cui è facile sbagliare. Supponi di essere in classe durante la verifica, il tempo a disposizione sta per terminare e tu, senza la possibilità di usare la calcolatrice, dovresti:
- Scegliere il corretto fattore di riduzione.
- Eseguire in modo corretto le divisioni.
- Procedere ulteriormente a dividere fino ad arrivare a una frazione ridotta ai minimi termini.
- Tutto questo senza commettere errori.

Siamo d’accordo, ognuno è libero di seguire il procedimento che preferisce. C’è da considerare però un paio di cose. Noi siamo partiti da una moltiplicazione in cui erano presenti solo due frazioni. Negli esercizi che ti verranno assegnati e anche nella verifica, ci saranno quasi sicuramente moltiplicazioni con tre o quattro frazioni. E la cosa si fa molto complicata seguendo questo procedimento.
Inoltre nella consegna ci può essere scritto espressamente: calcola il risultato delle seguenti moltiplicazioni applicando la semplificazione in croce. Per cui il procedimento appena descritto, anche se corretto non è percorribile.
Procedimento consigliato
Vediamo adesso cosa otteniamo se semplifichiamo in croce. Ti ricordo che semplificare in croce vuol dire dividere per lo stesso numero il numeratore di una frazione e il denominatore di un’altra frazione.
In questo caso è possibile dividere per 5 il numeratore della prima frazione (5) e il denominatore della seconda frazione (10). Le operazioni che devo fare sono:
5 : 5 = 1 e 10 : 5 = 2

Possiamo anche dividere il denominatore della prima frazione (18) e il numeratore della seconda frazione (9) per 9. Le operazioni che andremo a eseguire sono:
18 : 9 = 2 e 9 : 9 = 1

Adesso non ci rimane che moltiplicare tra loro i numeratori e moltiplicare tra loro i denominatori. Le operazioni che dobbiamo eseguire sono:
1 · 1 = 1 e 2 · 2 = 4
Per cui il risultato che otteniamo è:
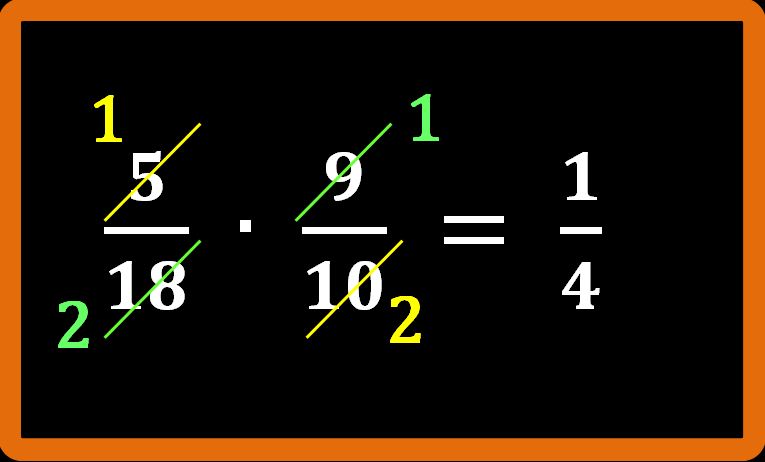
Ripeto, ognuno è libero di seguire il procedimento che preferisce, ma oggettivamente sapere semplificare in croce rende tutto molto più semplice. Non abbiamo eseguito nessuna divisione particolarmente difficile, tutti i calcoli erano talmente facili da non necessitare la calcolatrice. Per cui semplificare in croce è un procedimento molto consigliato.
Concludiamo questo articolo in cui abbiamo visto un altro esempio di semplificazione in croce spiegando perchè si chiama così. Si chiama semplificazione in croce perchè se colleghiamo le frazioni coinvolte nelle divisioni, otteniamo una croce:

Su Youtube
Su Youtube puoi trovare sia l’esercizio appena svolto, sia altri esercizi. Se ti sono utili, iscriviti al nostro canale.
Link utili
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe.Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli.Se vuoi ripassare l’alfabeto greco puoi visitare questa pagina.
Se hai domande o vuoi segnalare un errore puoi lasciare un commento o contattarmi alla casella mail matematica.facile@libero.it