In un articolo precedente abbiamo visto alcuni esempi di scomposizione in fattori primi. In questo articolo vedremo altri esempi di scomposizione in fattori primi. Più esercizi svolgi, meno errori commetterai. Sbagliare è normale, anzi è proprio sbagliando che si impara. L’importante è non arrendersi e continuare a provare fino a quando non si riesce.
Indice
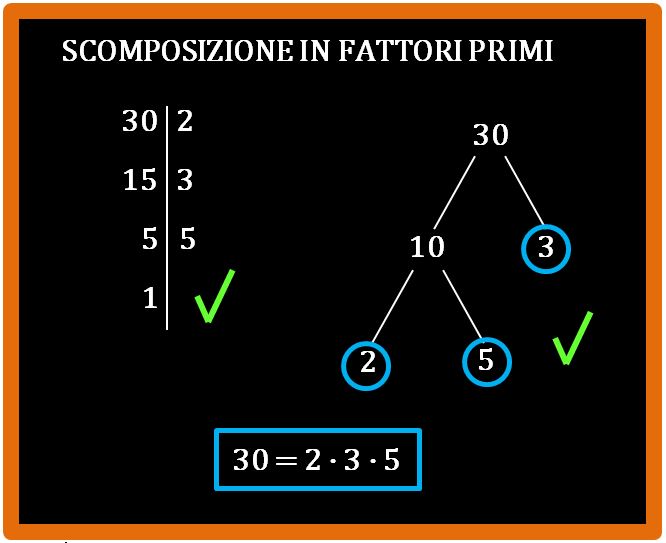
Esempio 4: scomposizione in fattori primi del 66
Scomponiamo il numero 66.
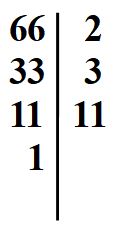
Scriviamo ora il numero 66 come prodotto di fattori primi.
66 = 2 · 3 · 11
Questo è il risultato che stavamo cercando.
Esempio 5
Scomponiamo il numero 126. Prima prova da solo. Poi controlla se quello che hai ottenuto corrisponde a quello che leggi sotto.
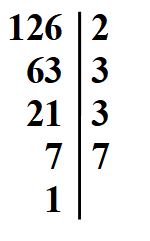
Scriviamo il 126 come prodotto di fattori primi usando la scrittura esponenziale.
126 = 2 · 32 · 7
Questo è il risultato che stavamo cercando.
Esempio 6
Scomponiamo il numero 84. Prova tu. Poi controlla il risultato che hai ottenuto con quello che puoi leggere sotto.
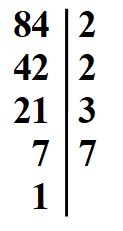
Scriviamo il numero 84 come prodotto della scomposizione in fattori primi, usando la scrittura esponenziale.
84 = 22 · 3 · 7
Questo è il risultato che stavamo cercando.
Scomposizione ad albero
Cominciamo ora a vedere come funziona la scomposizione ad albero.
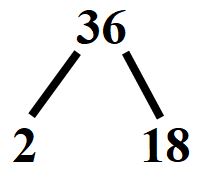
Esempio 7: scomposizione ad albero del numero 36
Scomponiamo il numero 36. Possiamo dividerlo per 2, ma ricorda che non c’è una regola precisa. Puoi scegliere di dividerlo per 3 o per 4. L’ importante è eseguire correttamente le divisioni.
Dividiamo quindi per 2. Scriveremo in questo modo: il due a sinistra sotto il 36 e il risultato della divisione a destra.
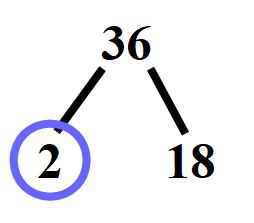
Il numero due è un numero primo e lo evidenziamo con un cerchio, io preferisco il colore blu, ma tu puoi scegliere un colore qualsiasi. Se non ti ricordi cosa sono i numeri primi puoi dare un’ occhiata al mio articolo i numeri primi e i numeri composti.
Il numero 18 invece è un numero composto, quindi dobbiamo continuare a dividere. Non c’è una regola precisa per scegliere il numero per cui dividere. Se il numero è pari, io preferisco dividere per 2. Scriveremo, come abbiamo fatto prima, il 2 a sinistra sotto il 18; invece il risultato della divisione sotto il 18, ma a destra: in questo modo.
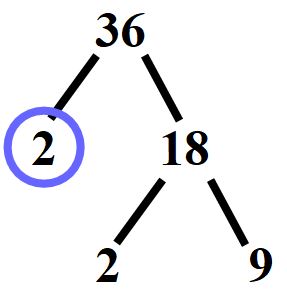
Procediamo come sopra. Il numero 2 è un numero primo e lo cerchiamo. Il 9 è un numero composto e lo dividiamo.
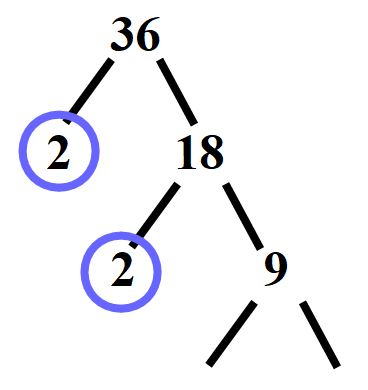
Il numero 9 non è un numero pari, non possiamo dividerlo per 2, ma possiamo dividerlo per 3. Scriveremo il risultato della divisione sotto il 9, a destra.
Scriveremo in questo modo.
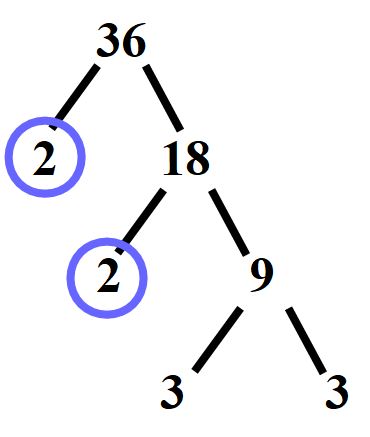
Come risultato della divisione otteniamo 3.
Il numero 3 è un numero primo, quindi dobbiamo cerchiarlo. Ricorda, vanno cerchiati solo i numeri primi. Andremo a tracciare un cerchio sopra tutti e due i 3.
Scriveremo così:
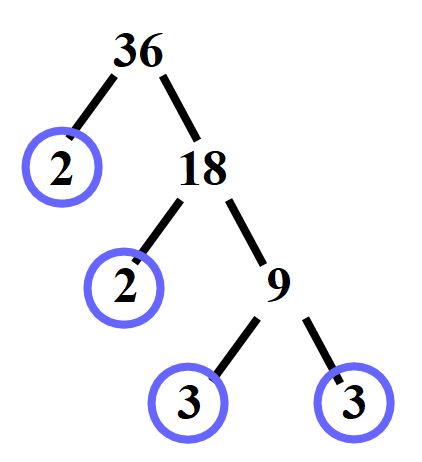
Non possiamo più procedere con le divisioni, questo vuol dire che abbiamo terminato con la scomposizione.
Non ci resta che scrivere il 36 come prodotto di fattori primi:
36 = 2 · 2 · 3 · 3
È più corretto usare la scrittura esponenziale:
36 = 22 · 32
Questo è il risultato che stavamo cercando. Se ci hai fatto caso è uguale al risultato che abbiamo trovato con la scomposizione in colonna. Sono due strade diverse, ma entrambe corrette, per arrivare allo stesso risultato.
Esempio 8: scomposizione ad albero del numero 36, metodo alternativo
Come ti ho già detto, quando devi scegliere il numero per cui vuoi dividere, non esiste una regola. Io preferisco dividere per 2, ma la tua prof probabilmente preferisce un altro numero. Sono comunque due strade corrette.
Continuiamo con altri esempi di scomposizione in fattori primi. Faremo ora un esempio sempre con il numeo 36, in cui però seguiremo una strada diversa.
Iniziamo subito e invece di dividere per 2 come nell’esempio di prima, dividiamo il 36 per 6.
Scriveremo allora il 6 sotto il 36 a sinistra.
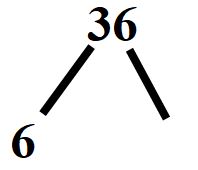
Invece scriveremo il risultato della divisione a destra, in questo modo.
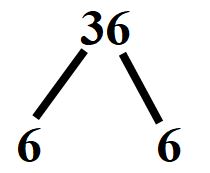
Bisogna ora fare attenzione. Ricordiamoci che noi vogliamo ottenere la scomposizione in fattori primi del numero 36.
Il numero 6 non è un numero primo, quindi non tracceremo nessun cerchio. Invece quello che dobbiamo fare è continuare a dividere. Li dobbiamo dividere entrambi. Io scelgo di dividere per 2.
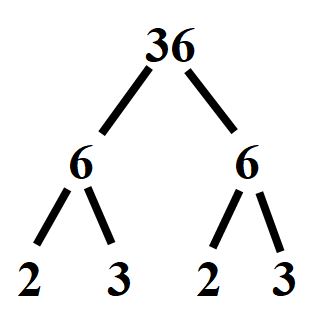
Scelta dei fattori primi
Possiamo ora andare a tracciare un cerchio nei numeri primi che abbiamo ottenuto come risultato.
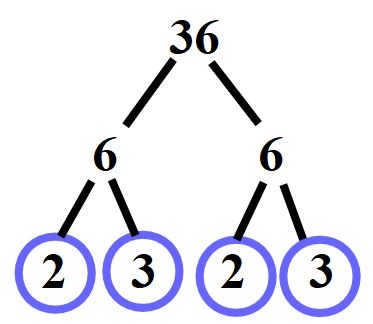
Come risultato delle divisioni abbiamo ottenuto tutti numeri primi.
Abbiamo quasi concluso l’esercizio, non ci rimane che scrivere in forma esponenziale il 36.
36 = 22 · 32
Ricordati, non ti preoccupare se per i primi esercizi ti sembra di impegare troppo tempo o se ti sembrano complicati. Abbiamo cominciato tutti così. Poi con l’allenamento ed esercitandoti, tutto diventerà più semplice, ma solo dopo un buon numero di esercizi.
Esempio 9
Vediamo ancora altri esempi di scomposizione in fattori primi. Scomponiamo il numero 150. Dobbiamo scegliere per quale numero dividerlo. So di averti detto che preferisco dividere per 2, ma in questo caso c’è una strada più veloce che ti indicherò tra poco.
Se ti ricordi, quando hai studiato i criteri di divisibilità c’era anche quello del 10, che era forse il più semplice: un numero è divisibile per 10 se termina per zero. È proprio il nostro caso, infatti l’ultima cifra del numero 150 è zero, questo vuol dire che è divisibile per 10.
Allora potremo scrivere il 10 sotto il 150 a sinistra e il risultato della divisione, sotto il 150 a destra, in questo modo.
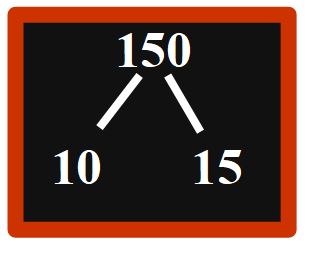
Ricorda, dobbiamo tracciare un cerchio solo nei numeri primi. Nè il 10, nè il 15 sono numeri primi, quindi dobbiamo procedere dividendo entrambi.
Io scelgo di dividere il 10 per 2. E divido il 15 per 3. Scriverò in questo modo.
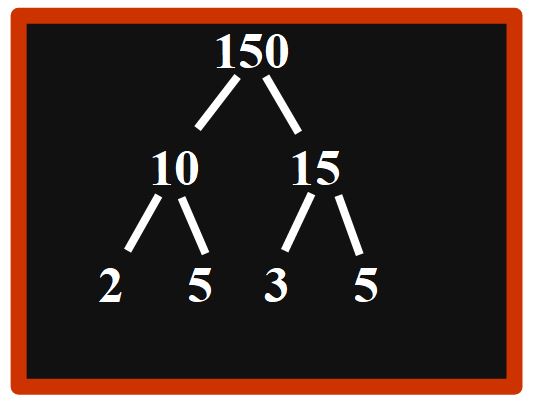
Bene, abbiamo eseguito le divisioni e abbiamo ottenuto come risultato tutti numeri primi (2, 3, 5) possiamo quindi cerchiarli.
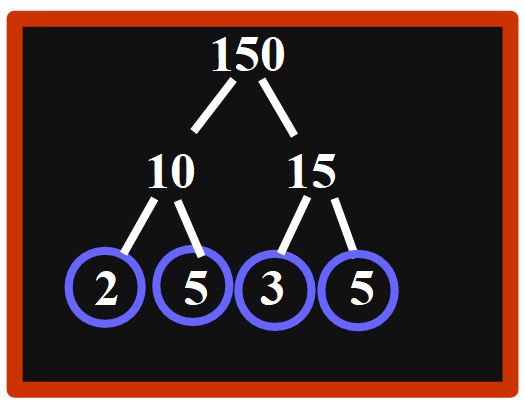
Abbiamo ottenuto i fattori di scomposizione del 150. Scriviamo allora il numero 150 come prodotto dei suoi fattori primi.
150 = 2 · 3 · 52
Questo è il risultato che stavamo cercando. Esercizio concluso
link utili
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe. Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.