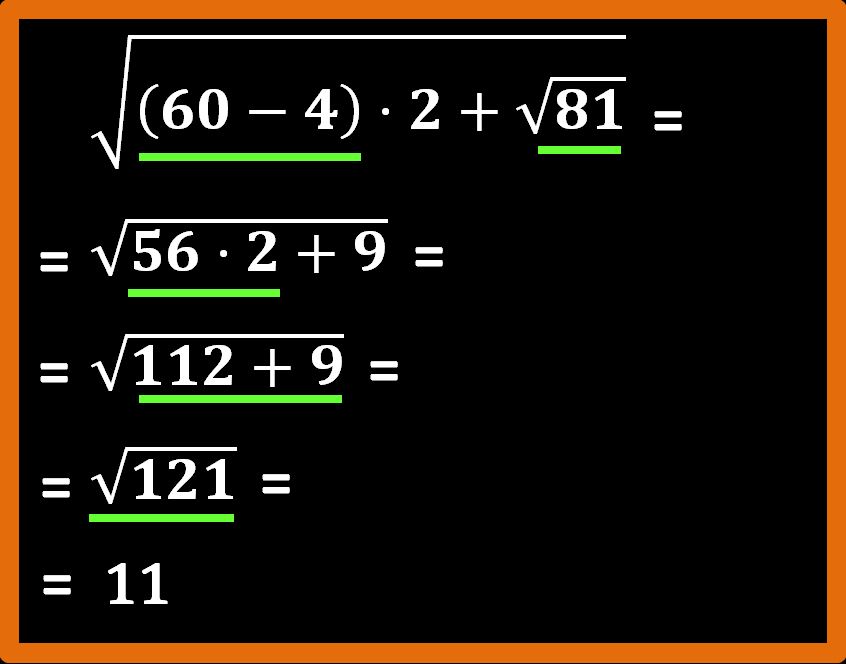Oggi in classe la tua prof ha spiegato i criteri di divisibilità, ma tu non eri tanto attento. Quando sei tornato a casa, hai provato a fare gli esercizi, ma non hai capito molto. Nessun problema, niente di difficile. Con 5 minuti di impegno, sarai in grado in pochi secondi di stabilire per esempio se 25784 è divisibile per 3 oppure no.
Per sapere cosa si intende per divisibilità ti consiglio di dare una lettura al mio articolo in cui parlo di numeri primi e divisibilità.
Indice
- A cosa servono i criteri di divisibilità
- Criterio di divisibilità per 2
- Criterio di divisibilità per 3
- Criterio di divisibilità per 5
- Su Youtube
- Criterio di divisibilità per 10
- Altri criteri di divisibilità
- Esercizi in pdf
A cosa servono i criteri di divisibilità
Forse ti sei chiesto a cosa servono e cosa sono questi criteri di divisibiltà. I criteri di divisibilità sono dei modi semplici e a volte anche divertenti per sapere se un numero è divisibile per un altro. Per esempio è possibile sapere se 591 è divisibile per 3 senza eseguire la divisione, ma con un calcolo molto più semplice e rapido che vedremo tra poco.
Tra le altre cose, questi criteri sono utili quando studierai la scomposizione in fattori primi (che puoi trovare in questo articolo), quando dovrai calcolare il minimo comune multiplo tra due o più numeri, quando dovrai ridurre una frazione ai minimi termini e in molti altri argomenti. Quindi conoscerli bene è molto utile.
Ma cominciamo a vedere quali sono e come funzionano i criteri di divisibilità.
Criterio di divisibilità per 2
Mentre in classe la tua prof spiegava la divisibilità per 2, tu pensavi ad altro e non sei riuscito a capire come funziona questo criterio. Niente paura. Per sapere se un numero è divisibile per 2 è sufficiente guardare l’ultima cifra.
Per esempio:
- nel numero 1598 l’ultima cifra è 8;
- nel numero 3590 l’ultima cifra è 0;
- nel numero 3254 l’ultima cifra è 4;
- nel numero 5863 l’ultima cifra è 3.
Se l’ultima cifra è una di queste:
0 – 2 – 4 – 6 – 8
allora il numero è divisibile per 2.
Torniamo a dare un’occhiata agli esempi di poco fa.
- nel numero 1598 l’ultima cifra è 8; è divisibile per 2;
- nel numero 3590 l’ultima cifra è 0; è divisibile per 2;
- nel numero 3254 l’ultima cifra è 4; è divisibile per 2;
- nel numero 5863 l’ultima cifra è 3; non è divisibile per 2.

Tutti quei numeri che finiscono con una delle cifre che abbiamo visto sopra (0; 2; 4; 6; 8 ) sono chiamati numeri pari. Possiamo allora dire che i numeri pari sono divisibili per 2.
Quindi, per essere sicuri di avere capito, ti suggerisco di prendere carta e penna e di riscrivere i numeri che trovi sotto. Facciamo un semplice esercizio:

Traccia un cerchio attorno ai numeri divisibili per 2, oppure detto in modo diverso cerchia i numeri pari (cioè quelli in cui l’ultima cifra è una di queste: 0; 2; 4; 6; 8 ). Se hai lavorato bene hai ottenuto il risultato che trovi sotto.

L’immagine animata sotto, illustra quello che abbiamo appena detto.

Criterio di divisibilità per 3
Vediamo adesso un modo facile per capire se un qualsiasi numero è divisibile per 3. Facciamo un esempio, vogliamo stabilire se 7854 è divisibile per 3. Per il momento l’unico modo che conosciamo è quello di eseguire la divisione 7854:3
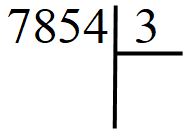
È una divisione lunga da svolgere. Stai forse pensando che potresti usare la calcolatrice, ma in classe non puoi di certo usarla. Per fortuna il criterio di divisibilità ci aiuta.
Per capire se 7854 (si legge settemilaottocentocinquantaquattro) è divisibile per 3 dobbiamo sommare le cifre di cui è composto il numero e vedere se il risultato è un multiplo di 3. Ti stai chiedendo quali sono i multipli di 3? La risposta è: la tabellina del 3. Ripassiamola:
3 – 6 – 9 – 12 – 15 – 18 – 21 – 24 – 27 – 30 …
Bene, ora che abbiamo ripassato la tabellina del 3 e quindi sappiamo quali sono i multipli di 3 (almeno quelli che ci servono) facciamo un esempio con i numeri.
Voglio sapere se il numero 7854 è divisibile per 3. Quelo che devo fare è sommare le cifre che formano il numero 7854, in altre parole devo eseguire questa somma:
7 + 8 + 5 + 4 = 24
Abbiamo ottenuto come risultato 24. Ora dobbiamo chiederci:
24 è un multiplo di 3?
Andiamo a controllare tra quelli che abbiamo scritto.
3 – 6 – 9 – 12 – 15 – 18 – 21 – 24 – 27 – 30
Effettivamente 24 è un multiplo di 3. Questo vuol dire che 7854 è divisibile per 3. Chiaro? Forse si e forse no. Facciamo altri esempi? Meglio.
Esempi di divisibilità per 3
Esempio 1
Stabiliamo se il numero 582 è divisibile per 3. Dobbiamo sommare le cifre che lo formano.
5 + 8 + 2 = 15
Abbiamo ottenuto come risultato 15.
La domanda che dobbiamo porci ora è:
15 è multiplo di 3?
Ripassiamo la tabellina del 3 ed ecco la risposta.
3 · 5 = 15, allora è multiplo di 3.
Questo ci dice che 582 è divisibile per 3.
Ti stai di nuovo chiedendo a cosa servono i criteri di divisibilità? Non ne vedi l’utilità? Ti accorgerai di quanto sono utili quando studierai la scomposizione in fattori primi.
Esempio 2
Continuiamo con gli esempi. Stabiliamo se 801 è divisibile per 3.
Sommiamo le cifre che compongono il numero 801.
8 + 0 + 1 = 9
Dobbiamo chiederci se 9 è multiplo di 3. La risposta è sì, infatti 3 · 3 = 9. Allora 801 è divisibile per 3. Fantastico, andiamo avanti.
Esempio 3
Cerchiamo di capire se 457 è divisibile per 3.
4 + 5 + 7 = 16
Il risultato della somma è 16. Dobbiamo chiederci: 16 è un multiplo di 3? Oppure detta in un altro modo: 16 è divisibile per 3? La risposta è ‘No’. Questo vuol dire che il numero 457 non è divisibile per 3.
Vedi come senza eseguire nessuna divisione riusciamo a capire se un numero qualsiasi è divisibile per 3 oppure no. E ci riusciamo con una semplice somma. Un ultimo esempio
Esempio 4
Ci chiediamo se 6794 è divisibile per 3. Sommiamo le cifre che lo compongono.
6 + 7 + 9 + 4 = 26
Ora dobbiamo stabilire se 26 è multiplo di 3. Se non ti ricordi la tabellina, puoi ripetere con il 26 lo stesso procedimento usato per il 6794, cioè sommiamo le cifre di che formano il 26
2 + 6 = 8
Il numero 8 non è divisibile per 3, questo vuol dire che 6794 non è divisibile per 3.
Criterio di divisibilità per 5
Passiamo adesso a studiare quello che ritengo sia il più semplice tra i criteri di divisibilità, quello per 5.
La regola è questa:
‘Un numero è divisibile per 5 se finisce per 0 oppure per 5‘.
Tutto qua, finito. Facciamo un esercizio per capire meglio la regola. Prendi carta e penna e riscrivi i numeri qui sotto.
Esempio 1

Adesso fai un cerchio attorno a quei numeri che finiscono con 5 oppure con 0. Se hai lavorato bene hai ottenuto il risultato che vedi sotto.

Esercizio concluso. I numeri 10, 35, 40, 55, 60 e 100 sono divisiibili per 5, tutti gli altri non lo sono.
Esempio 2
Solo per essere proprio certi di avere capito, facciamo un altro esempio.

Dobbiamo trovare i numeri divisibili per 5. Ricordiamoci che sono divisibili per 5 tutti quei numeri in cui l’ultima cifra è 5 oppure 0. Andiamo quindi a tracciare un piccolo cerchio nei numeri che ci interessano.

Esercizio concluso.
Criterio di divisibilità per 10
Se il criterio di divisibilità per 5 ti è sembrato semplice, allora quello per 10 ti sembrerà semplicissimo.
La regola dice questo:
‘Un numero è divisibile per 10 se la sua ultima cifra è 0‘.
Tutto qua. Troppo facile? E in effetti è facilissimo, ma è così. Facciamo un esempio:
Esempio 1

Ricorda: l’ultima cifra deve essere zero.

Esercizio concluso.
Altri criteri di divisibilità
Esistono anche altri criteri di divisibilità (per 4, per 7, per 9), ma alle scuole medie è sufficiente conoscere bene quelli che hai appena letto e naturalmente saperli usare.
Esercizi in pdf
Adesso possiedi gli strumenti necessari per lavorare con i criteri di divisibilità. Se vuoi, puoi provare a eseguire gli esercizi che trovi nel file pdf sotto. Lavora senza fretta, non stai facendo una gara di velocità. E non ti preoccupare se sbagli. Sbagliando si impara.
![]() Criteri di divisibilità – Esercizi.pdf
Criteri di divisibilità – Esercizi.pdf
Buon lavoro.
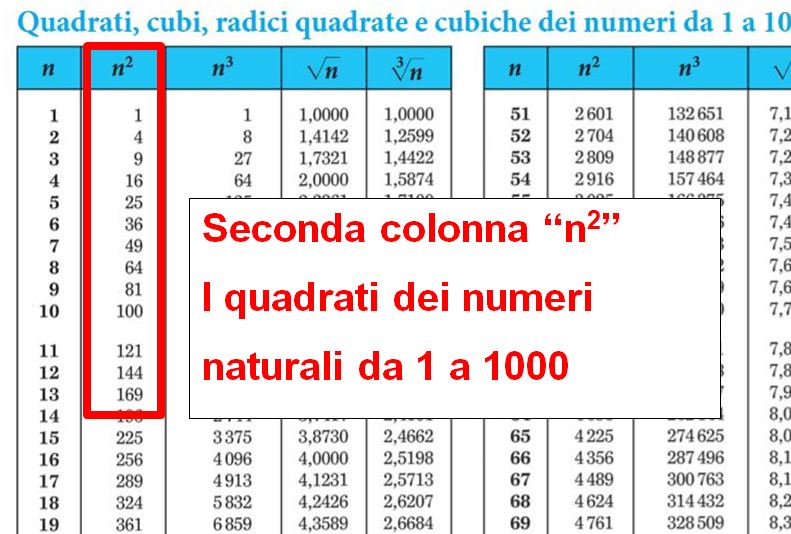
A questo link della Casa Editrice Zanichelli trovi le Tavole Numeriche. Puoi semplicemente visualizzarle oppure anche scaricarle sotto forma di file pdf facendo click sull’icona che trovi in alto a destra del documento.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.