Cara mamma, oggi il tuo pargolo è tornato da scuola dicendo che la prof aveva spiegato un argomento che non aveva capito. Hai guardato nel diario e ti sei resa conto che l’argomento spiegato era come ridurre ai minimi termini una frazione. Argomento di cui tu non ricordi molto. Nessun problema, con 5 minuti di impegno sarà tutto più chiaro.
Indice
- Breve ripasso sulle frazioni equivalenti
- Primo esempio
- Secondo esempio
- Terzo esempio
- Quarto esempio: il fattore di riduzione
- Esercizi
- Esercizi in pdf
Iscriviti al nostro canale youtube: matematicafacile
Breve ripasso sulle frazioni equivalenti
In un articolo precedente abbiamo parlato delle frazioni equivalenti e abbiamo visto come si può passare da una frazione a un’altra frazione equivalente. In questo articolo invece cercheremo di capire cosa vuol dire semplificare e ridurre ai minimi termini una frazione.
Se hai letto l’articolo sulle frazioni equivalenti avrai capito che se dividiamo il numeratore e il denominatore di una frazione per lo stesso numero naturale, otteniamo una frazione equivalente alla prima (cioè che ha lo stesso valore). Ripassiamo un poco prima di cominciare. Se non ti ricordi quali sono i numeri naturali, potresti andare a leggere il mio articolo su i numeri naturali.
Partiamo dalla frazione quattro sesti (che si può anche leggere quattro su sei oppure quattro fratto sei).
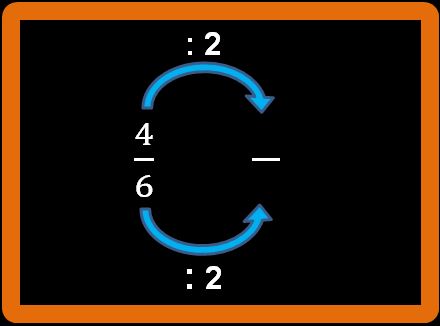
Dividiamo sia il 4 (numeratore) che il 6 (denominatore) per 2.
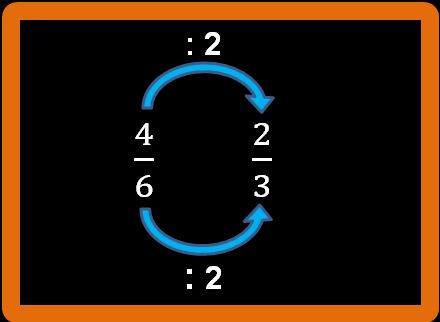
Otteniamo una nuova frazione, due terzi, che è equivalente alla prima (infatti se provi a fare con la calcolatrice 4 diviso sei e poi 2 diviso 3 otterrai lo stesso risultato). La differenza è che al numeratore e al denominatore compaiono numeri più piccoli.
Per vedere meglio che le due frazioni sono equivalenti possiamo aiutarci con dei modelli geometrici. Disegniamo su un foglio a quadretti (o una lavanga a quadretti) due rettangoli lunghi 12 quadretti. Dividiamo il primo rettangolo in 6 parti uguali e ne coloriamo 4 (questo primo rettangolo rappresenta la frazione quattro sesti). Dividiamo invece il secondo rettangolo in 3 parti uguali e ne coloriamo 2 (questo secondo rettangolo rappresenta la frazione due terzi).
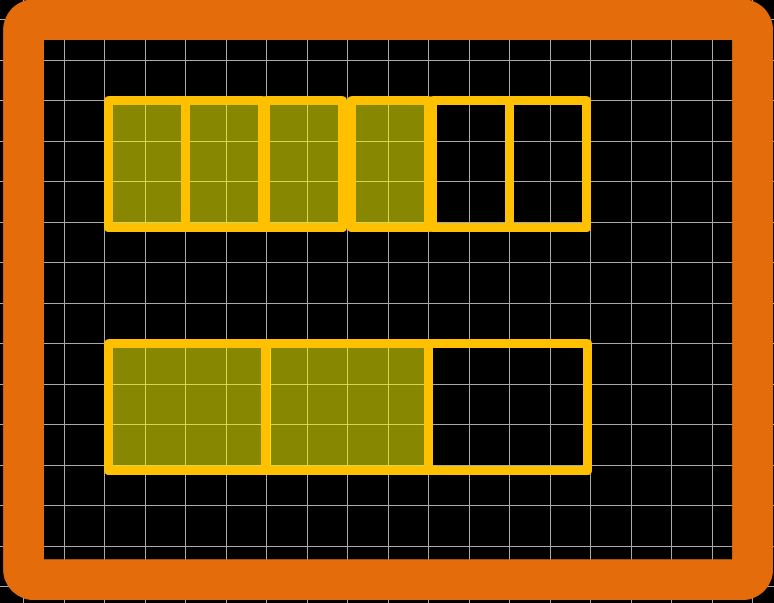
Se andiamo a contare i quadratini colorati vedremo che sono gli stessi sia nel primo, sia nel secondo rettangolo, ma le frazioni che rappresentano le parti colorate hanno numeri diversi.
Iscriviti al nostro canale YouTube
Ridurre ai minimi termini
Bene, una volta che abbiamo ben chiaro cosa sono le frazioni equivalenti, possiamo iniziare a spiegare come si può ridurre ai minimi termini una frazione e per quale motivo è importante saperlo fare.
esempio 1
Scriviamo la frazione 24 su 36 e semplifichiamola.
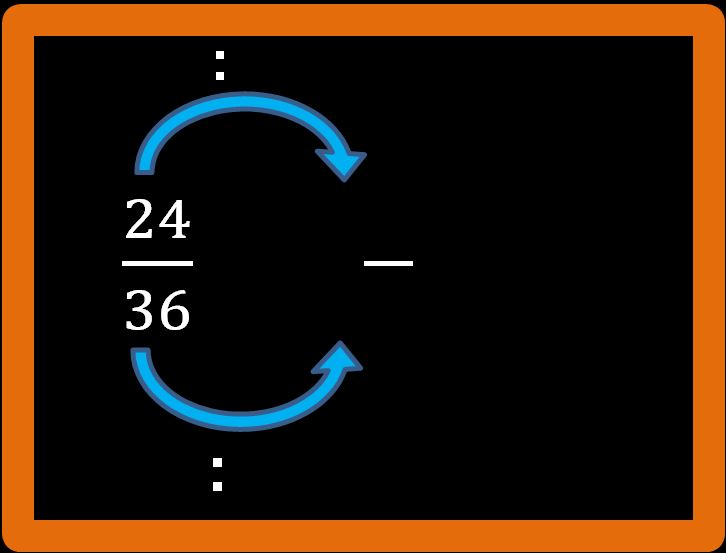
Ti ricordo che semplificare vuol dire dividere il numeratore e il denominatore per lo stesso numero. Io scelgo di dividere per 2 (in questo caso era anche possibile dividere per 3 o per 4). Se non ricordi i criteri di divisibilità potresti dare un’occhiata al mio articolo sui criteri di divisibilità.
Il risultato che otteniamo è il seguente: dodici diciottesimi.
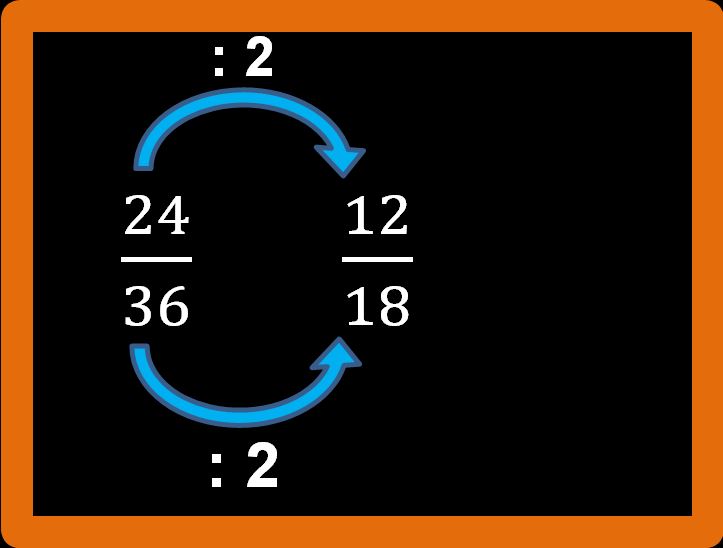
A questo punto dobbiamo chiederci: “È ancora possibile semplificare? Cioè, è possibile dividere ancora numeratore e denominatore per lo stesso numero?” Nel nostro esempio la risposta è SÌ. Possiamo dividere per 2.
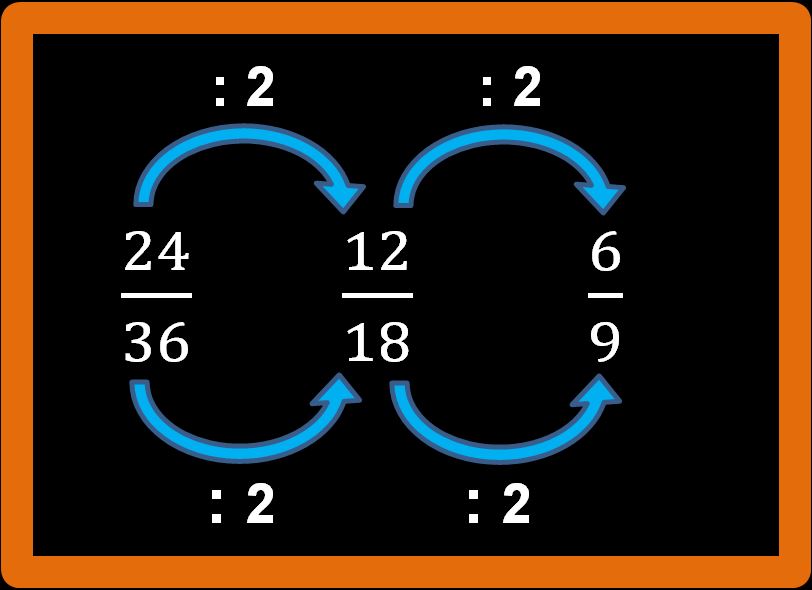
La domanda che dobbiamo porci è sempre la stessa: “Posso semplificare ancora?” E la risposta è ancora SÌ. Infatti è possibile dividere sia il numeratore (6) che il denominatore (9) per 3.
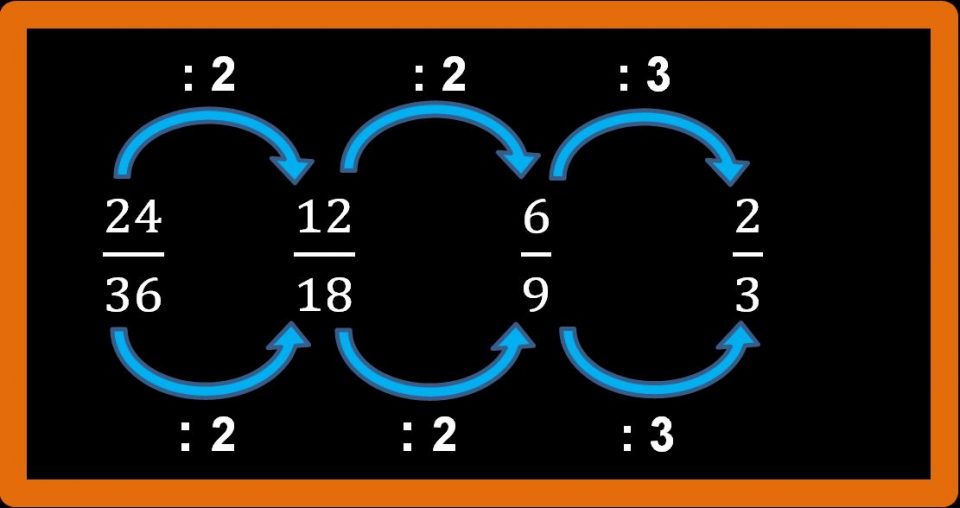
Abbiamo ottenuto la frazione due terzi. Dobbiamo sempre chiederci: “È possibile continuare a semplificare?” Questa volta la risposta è NO. Non è più possibile semplificare. Non è più possibile dividere numeratore e denominatore per lo stesso numero. Numeratore e denominatore sono numeri primi tra loro, cioè hanno come unico divisore comune il numero 1.
Allora possiamo dire che la frazione 2 su 3 è una frazione ridotta ai minimi termini.
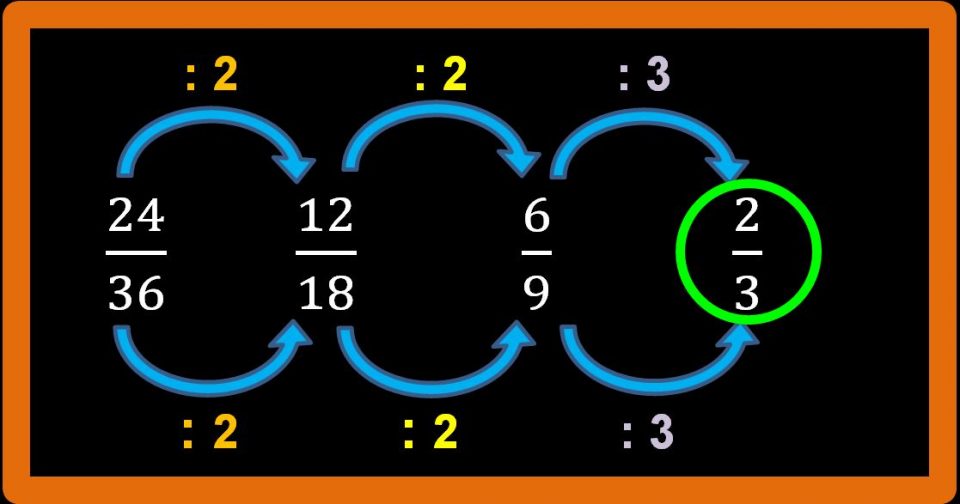
Ok, sono d’accordo. Potrà sembrarti un procedimento lungo, noioso e inutile. Ma quando ti troverai a eseguire una moltiplicazione tra frazioni, ti renderai conto che saper ridurre ai minimi termini è molto conveniente. È utile anche nelle divisioni tra frazioni, ti farà risparmiare tempo e ti aiuterà a commettere meno errori.
In generale, in tutta la matematica pratica, è preferibile lavorare con numeri piccoli. Questo è vero in una classe di seconda media, come è vero nei laboratori della NASA o del CERN di Ginevra. Ci sarà un motivo se è stata inventata la notazione esponenziale. (Il motivo è appunto lavorare e maneggiare numeri piccoli).
esempio 2
Facciamo un altro esempio. Riduciamo ai minimi termini la frazione 30 su 42. Ricorda dobbiamo dividere per lo stesso numero sia il numeratore che il denominatore. Il denominatore è divisibile per 3 e anche il numeratore, quindi possiamo procedere con le divisioni. Se non ti ricordi i criteri di divisibilità sarebbe meglio andarli a ripassare.
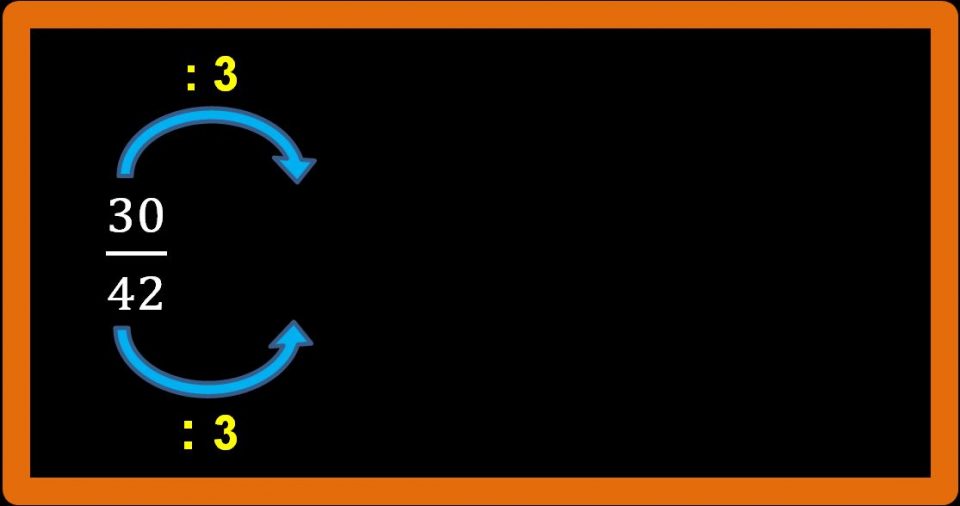
Otteniamo il seguente risultato:
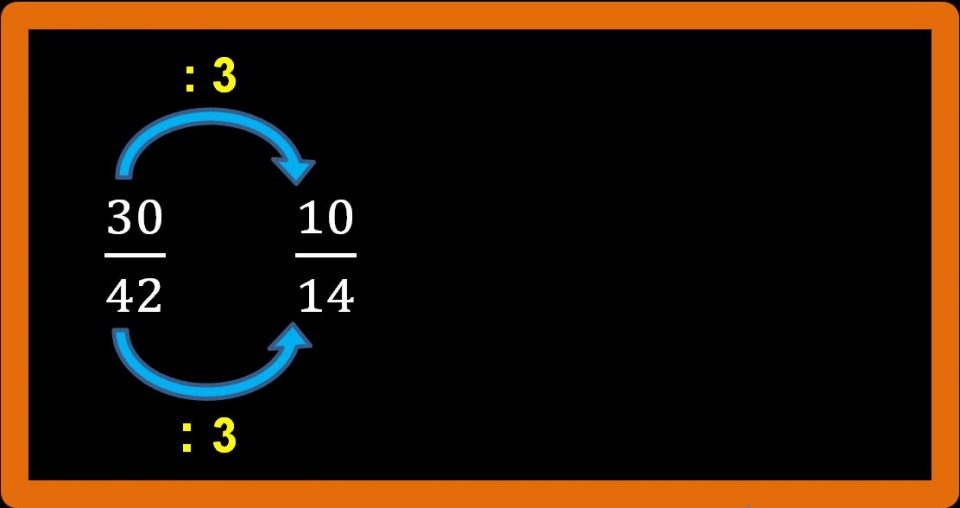
Quello che dobbiamo fare, è sempre chiederci se possiamo andare avanti con le semplificazioni. Potrei essere tentato di dividere il numeratore (cioè 10) per 5, ma il denominatore (14) non è divisibile per 5, quindi questa demplificazione non è possibile. Invece possiamo dividere sia il numeratore che il denominatore per 2.
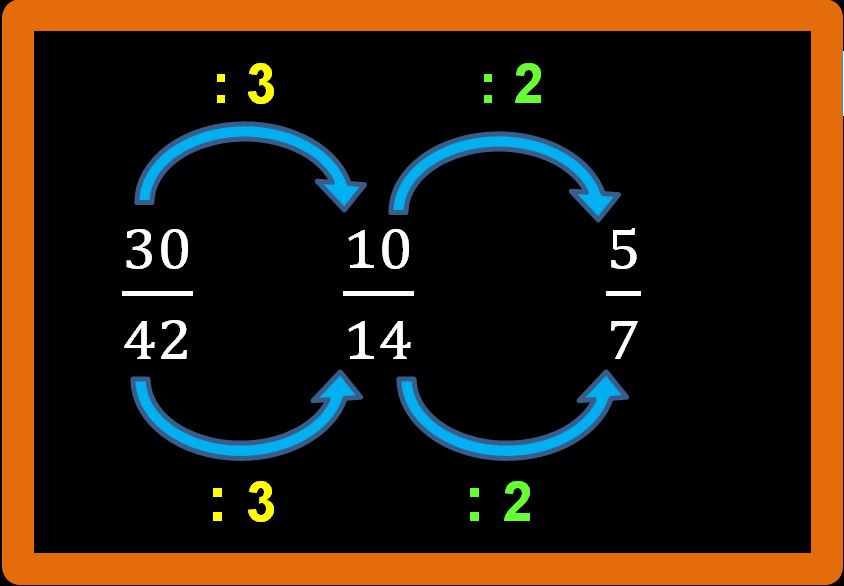
Molto bene, abbiamo ottenuto la frazione 5 su 7 (che si può anche leggere cinque settimi). Sia il 5 che il 7 sono numeri primi, questo ci aiuta a capire che non è più possibile andare avanti a semplificare. Cinque settimi è una frazione ridotta ai minimi termini.
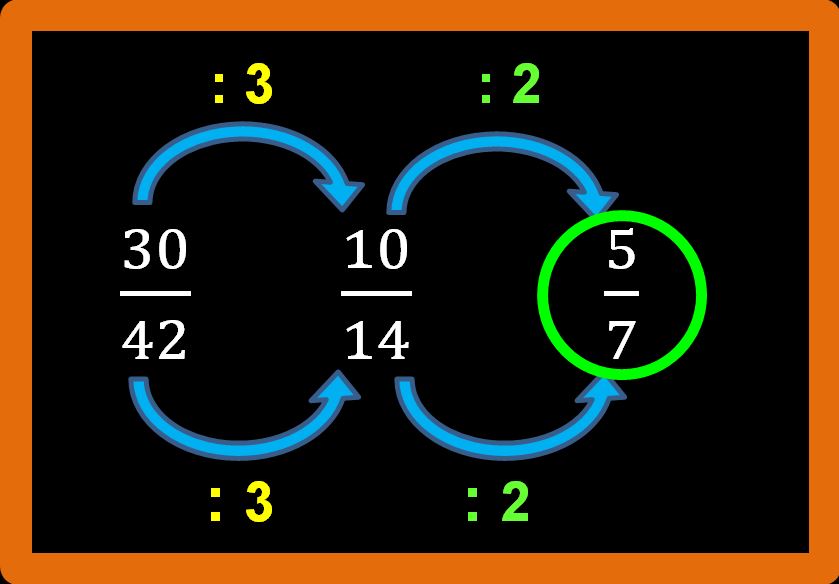
Esercizio concluso.
esempio 3
Proviamo a ridurre ai minimi termini la frazione cinquantatre centoventesimi.
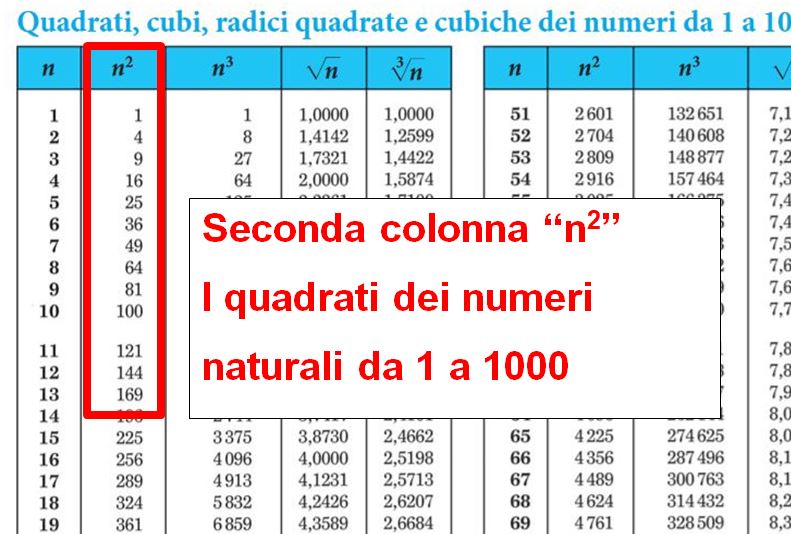
Il 53 è un numero primo, cioè è divisibile solo per 1 e per se stesso, non ha altri divisori. Se vuoi andare a ripassare i numeri primi, potresti dare un’occhiata all’articolo i numeri primi e i numeri composti. Non è necessario ricordare tutti i numeri primi a memoria, non sarebbe neanche possibile. Fortunatamente ci vengono in aiuto le tavole numeriche in cui sono elencati i numeri primi da 1 a 10000. Se non sai come si usano o dove si trovano le tavole numeriche, potresti leggere il mio articolo come si usano le tavole numeriche.
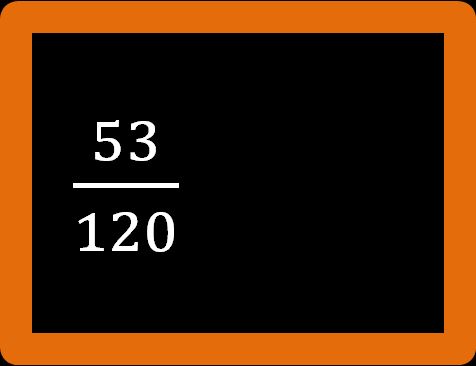
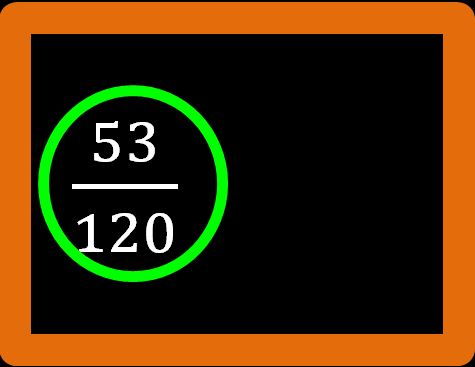
Il 120 al denominatore è divisibile per 2, 3, 4, 5 e 10. Ma il numeratore 53, come abbiamo già detto, non è divisibile per nessuno di questi numeri, infatti è un numero primo. Dato che numeratore e denominatore non possono essere divisi per lo stesso numero allora la frazione è già ridotta ai minimi termini.
Esempio 4: il fattore di riduzione
Dopo aver fatto qualche esempio e aver capito come semplificare e ridurre ai minimi termini una frazione, ti sarai reso conto che disegnare quelle frecce è poco conveniente perchè ci vuole molto tempo. Molti prima di te l’hanno pensata allo stesso modo e qualcuno si è inventato un modo veloce per scrivere quelle frecce. Vediamo qual è.

Invece di scrivere le frecce, si scrive un piccolo numero in alto a destra della frazione preceduto da una parentesi tonda, che viene chiamato fattore di riduzione. Quel numero vuol dire che dividiamo il numeratore e il denominatore per lo stesso numero naturale.
Abbiamo ottenuto la frazione 5 su 9. Poichè il 5 e il 9 non hanno nessun divisore in comune, allora possiamo dire che la frazione cinque noni (mi raccomando, non cinque alla nona, che è la nona potenza di cinque 59) è ridotta ai minimi termini.

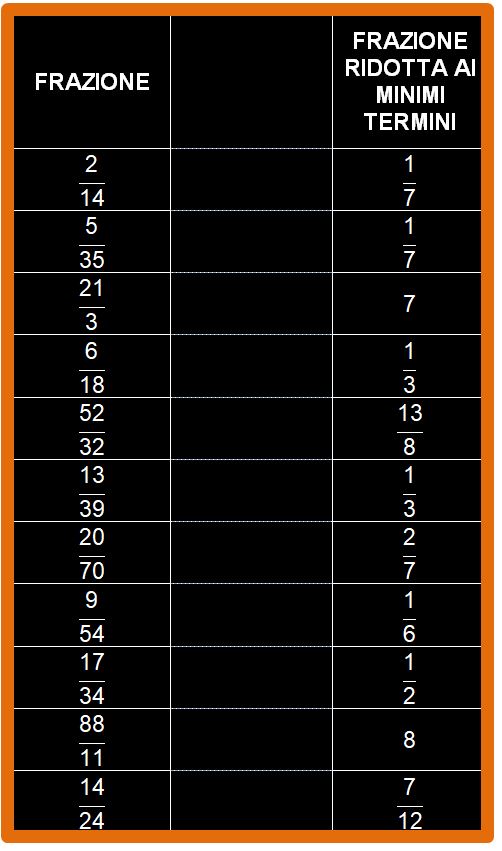
esercizi
Adesso possiedi tutti gli strumenti necessari per ridurre qualsiasi frazione ai minimi termini. Se vuoi puoi provare da solo a eseguire gli esercizi che vedi sotto. Non avere fretta, lavora con calma. Non è una gara di velocità. Trovi i risultati alla fine dell’articolo. I risultati ti servono per capire se hai lavorato bene oppure no.
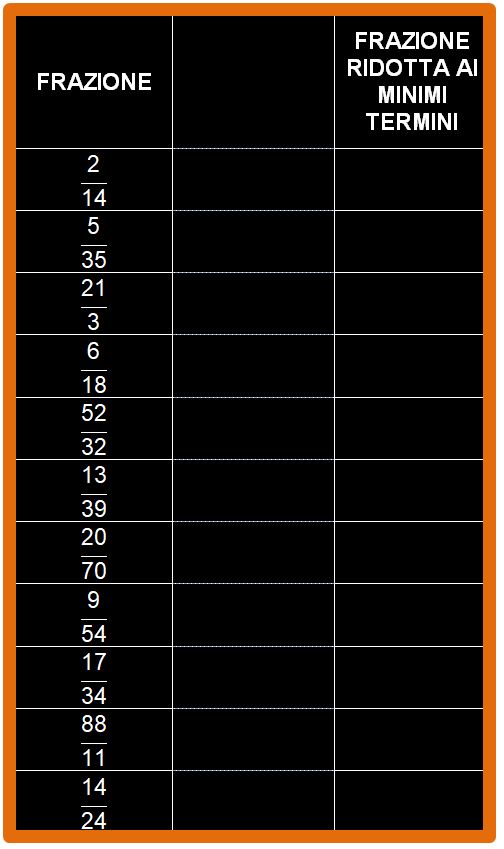
Buon lavoro e in bocca al lupo.
esercizi in pdf
Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto.
![]() Ridurre ai minimi termini una frazione – Esercizi.pdf
Ridurre ai minimi termini una frazione – Esercizi.pdf
![]() Ridurre ai minimi termini una frazione – Risultati.pdf
Ridurre ai minimi termini una frazione – Risultati.pdf
Buon lavoro.
A questo link della Casa Editrice Zanichelli puoi consultare e/o scaricare le tavole numeriche.
Se hai dubbi o vuoi segnalare un errore puoi lasciare un commento oppure puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
risultati