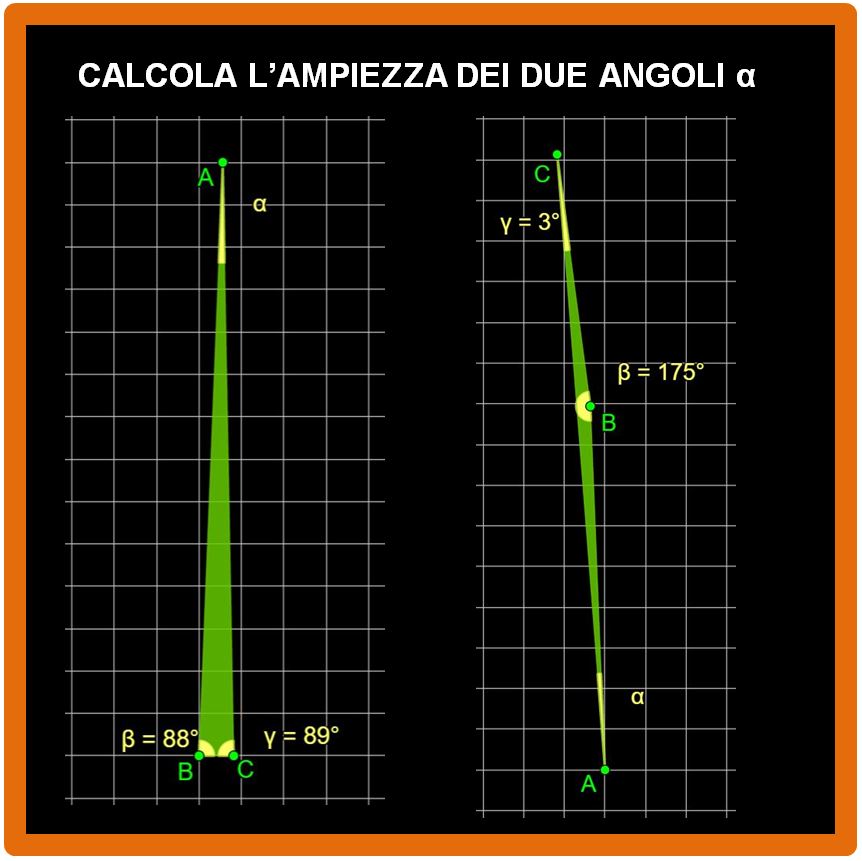
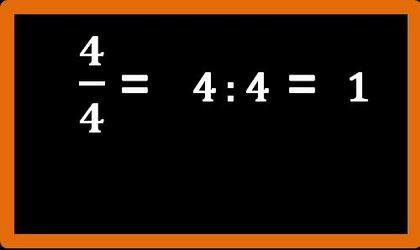Quando tuo figlio oggi è tornato da scuola era un po’ scuro in volto. Dopo una breve indagine hai scoperto che non aveva capito bene l’argomento che la prof di matematica aveva spiegato. Hai guardato sul diario e hai visto che la prof aveva spiegato le frazioni proprie, improprie e apparenti. Anche a te queste parole non dicono tanto. Niente paura. Dopo avere imparato cosa è una frazione, cosa sono numeratore e denominatore, in 5 minuti, ti sarà molto facile capire cosa sono le frazioni proprie, improprie e apparenti.
Partiamo un po’ da lontano. L’uomo ha da sempre la necessità di catalogare e classificare tutto. Si classificano i cibi (primi, secondi, dessert), i venti (brezza, burrasca, uragano), i terremoti (con la scala Mercalli o la scala Richter), i colori (con la scala RGB) e si classificano anche le frazioni. Classificare vuol dire creare dei gruppi in cui sistemare tutte le frazioni. Qualche matematico del passato ha creato tre gruppi in cui è possibile farle rientrare tutte. Questi tre gruppi sono quello delle frazioni proprie, quello delle frazioni improprie e quello delle frazioni apparenti. Questa premessa era d’obbligo, anche se un po’ noiosetta. Meglio passare ai numeri.
Indice
Frazioni proprie
Ora ti farò vedere alcuni esempi di frazioni:

Osservale bene. Guarda il numeratore e il denominatore di ogni frazione. In tutte le frazioni scritte alla lavagna il numeratore è sempre più piccolo del denomintore. Possiamo dare subito la regola:
“Una frazione in cui il numeratore è minore del denominatore è detta frazione propria”.
Tutto qua.
Naturalmente, dato che i numeri sono infiniti, è possibile scrivere infinite frazioni proprie:

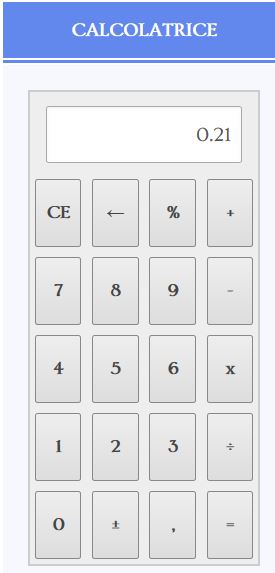
Tutto qua. Queste sono le frazioni proprie. Tutte le frazioni proprie indicano una quantità minore di 1. Se provi a eseguire con la calcolatrice 3 : 97 oppure 21 : 100 oppure 1 : 16 il risultato sarà sempre un numero minore di 1, che nella calcolatrice sarà 0, _ _ _ _ _. Per esempio 21 : 100 = 0,21
Frazioni improprie
Guarda invece queste frazioni:
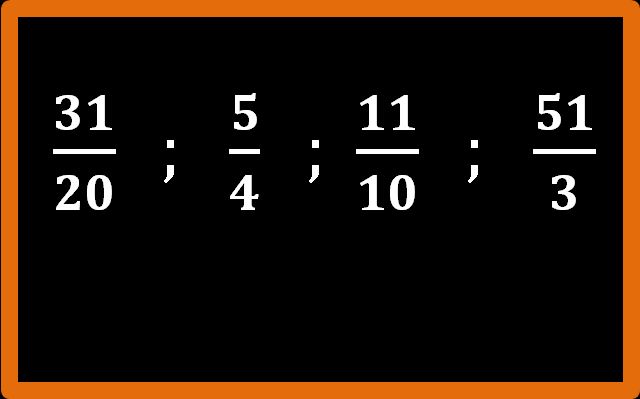
Come avrai già intuito, nelle frazioni scritte alla lavagna il numeratore è maggiore del denominatore. Quindi possiamo ricavare la regola: “Una frazione si dice impropria se il numeratore è maggiore del denominatore”. Anche in questo caso si possono scrivere infiniti esempi:

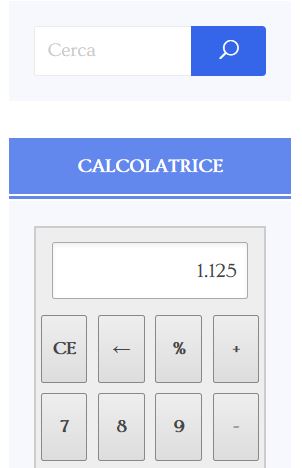
Le frazioni improprie rappresentano sempre quantità maggiori di 1. Prova a fare con la calcolatrice 9 : 8 otterrai come risultato 1,125
Per capire il significato delle frazioni improprie immaginiamo di andare in pizzeria con i prof. Il prof di religione e la prof di arte ordinano la stessa pizza e la dividono in 4 tranci uguali.
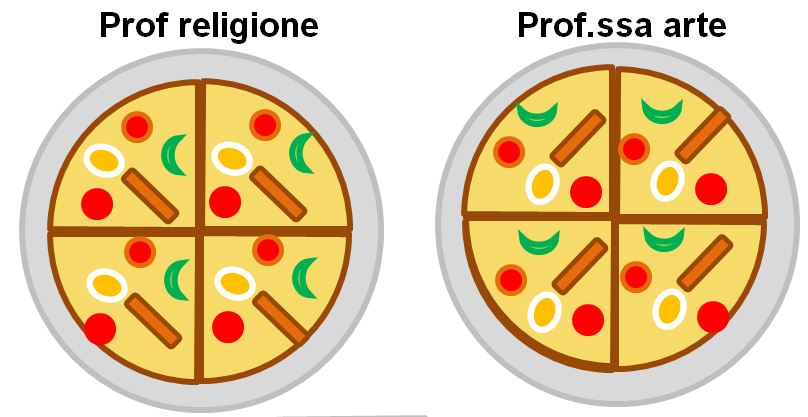
Il prof di religione mangia tutta la sua pizza. Invece la prof di arte non riesce a mangiare tutta la sua pizza, ne mangia tre pezzi. Quindi la situazione è questa:
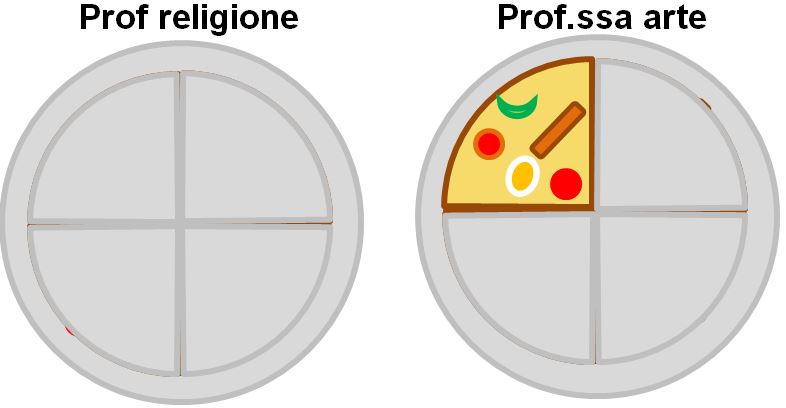
Al prof di relogione però la pizza è piaciuta talmente tanto che chiede alla prof di arte se può anche mangiare il pezzo che lei aveva lasciato. La prof acconsente. Quindi a fine serata il prof di religione avrà mangiato i suoi 4 pezzi più il pezzo lasciato dalla prof di arte. In totale il prof ha mangiato 5 pezzi di pizza. Ma la pizza era divisa in 4 parti. Quindi volendo usare le frazioni:

Tre quarti è una frazione propria, invece cinque quarti è una frazione impropria.
Tutto qua.
Frazioni apparenti
E se numeratore e denominatore sono uguali? Ecco che abbiamo le frazioni apparenti. Ma attenzione anche la frazione dieci quinti è una frazione apparente, oppure sedici ottavi, oppure nove terzi. Dai un’occhiata all’articolo sulle frazioni apparenti se vuoi avere maggiori chiarimenti😉.
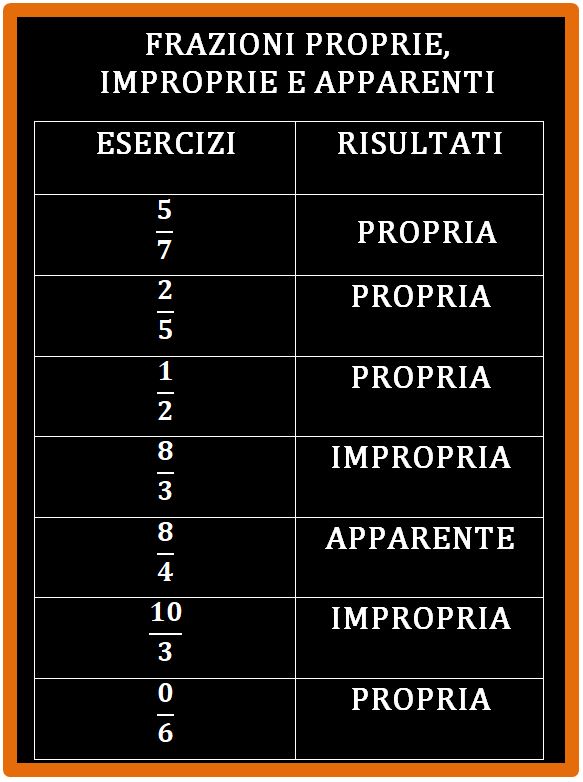
Esercizi
Adesso prova da solo. Ti consiglio di prendere carta e penna e copiare la tabella su un foglio. Lo so che ci vuole più tempo, ma scrivere equivale a leggere tre volte, per cui impareresti il meccanismo più in fretta. (Io farei così).
Nella casella vuota a fianco di ogni frazione devi scrivere se si tratta di una frazione propria, impropria o apparente. Non ti preoccupare se sbagli. Sbagliare è normale. L’errore fa parte del percorso di apprendimento. È come incontrare una buca per strada, può capitare. E poi nessuno verrà a rimproverarti. Trovi i risultati alla fine dell’articolo. I risultati ti servono per capire se hai fatto bene oppure no.
Buon lavoro.

Link utili
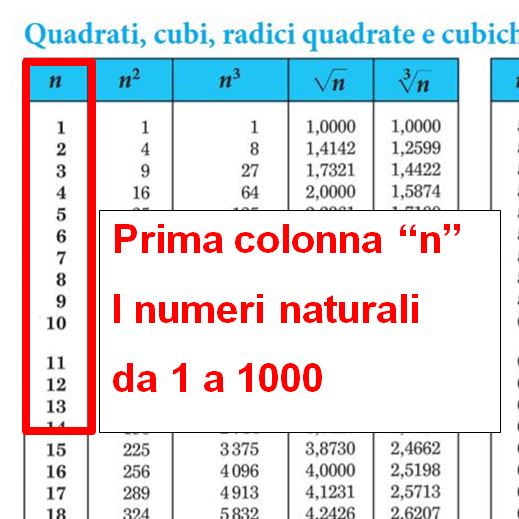
Le tavole numeriche sono uno strumento importante che ti può aiutare in diversi esercizi. Normalmente le trovi nel primo volume del libro di matematica. Se però le hai perse o nel tuo libro non c’erano, non preoccuparti. In questa pagina della Casa Editrice Zanichelli le puoi consultare. Puoi anche scaricarle come file pdf sul tuo pc seguendo le istruzioni che trovi alla fine di questo mio articolo.
Se hai dubbi o domande puoi lasciare un commento oppure puoi scrivere alla casella mail: matematica.facile@libero.it
Risultati