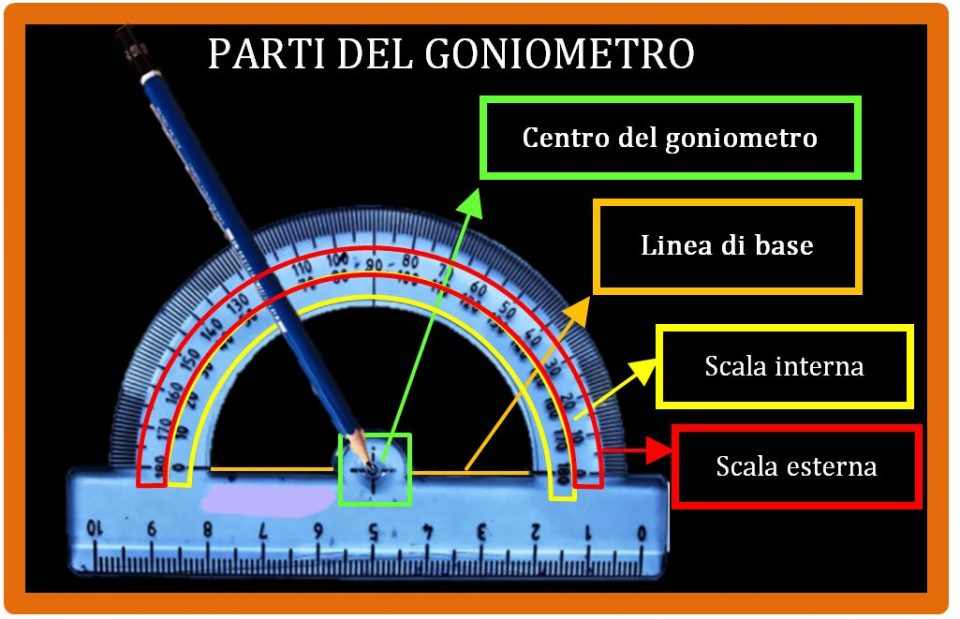
Ecco uno degli argomenti più incredibili della geometria. Prova a immaginare due triangoli molto diversi tra loro. Ecco, se con un goniometro misuri l’ampiezza dei loro angoli, ti accorgerai che la loro somma è la stessa. Adesso faremo alcuni esempi che ti faranno vedere come la somma degli angoli interni di un triangolo è sempre la stessa. Puoi anche vedere un esercizio svolto su Youtube.
angoli interni e angoli esterni
Prima di procedere dobbiamo essere sicuri di sapere qual è la differenza tra gli angoli interni e gli angoli esterni di un triangolo. La cosa è molto semplice, cominciamo disegnando un triangolo.
Gli angoli interni sono quelli che si trovano dentro il triangolo.
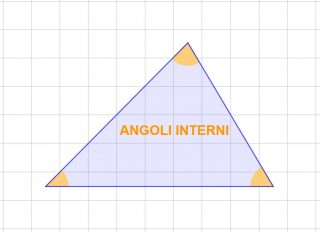
Invece, come avrai già capito, quelli esterni sono quelli che si trovano fuori dal triangolo.
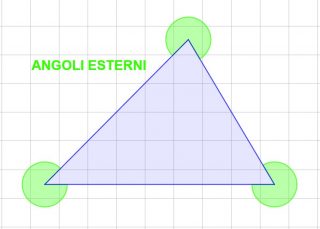
Riassumendo abbiamo:
A noi interessano solo gli angoli interni.
primo confronto
Verifichiamo che la somma degli angoli interni di un triangolo è sempre 180°. Prendiamo in considerazione due triangoli molto diversi: un triangolo rettangolo e un triangolo equilatero. Per disegnarli userò un programma gratis, che anche tu puoi scaricare sul tuo pc, si chiama GeoGebra Classico Versione 5. Lo puoi scaricare collegandoti alla pagina ufficiale del sito, cliccando qui.
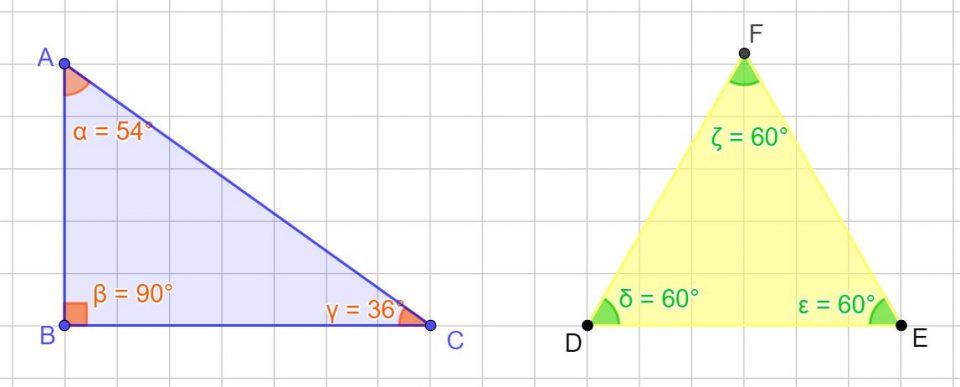
Somma angoli triangolo rettangolo
Cominciamo con il triangolo rettangolo. Osserviamo i suoi angoli:
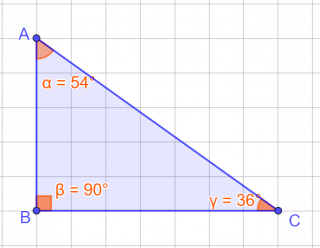α = 54°; β = 90°; γ = 36°;
Ti ricordo che per indicae gli angoli generalmente si usano le lettere dell’alfabeto greco. Se non ti ricordi come si chiamano, potresti dare un’occhiata a questa pagina della Casa Editrice Zanichelli.
Benissimo, adesso eseguiamo la somma dei tre angoli del triangolo rettangolo in figura:
α + β + γ = 54° + 90° + 36° = 180°
La somma dei tre angoli dà come risultato 180°.
Somma angoli triangolo equilatero
Passiamo al triangolo equilatero. Anche in questo caso osserviamo i suoi angoli. Dato che è equilatero, i suoi angoli sono tutti uguali tra di loro.
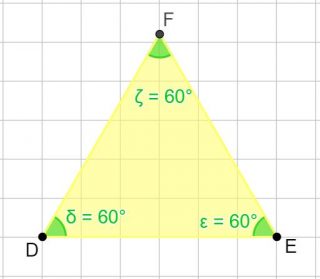δ = 60 °; ε = 60 ° ; ζ = 60° ;
Molto bene. Così come abbiamo fatto prima, eseguiamo la somma tra i tre angoli delta + epsilon + zeta
δ + ε + ζ = 60° + 60 ° + 60 ° = 180°
Anche in questo caso la somma dei tre angoli dà come risultato 180°.
Ma È sempre vero? secondo confronto
So cosa stai pensando, noi abbiamo preso in considerazione un triangolo rettangolo e un triangolo equilatero. E se invece consideriamo due triangoli qualsiasi, la somma degli angoli interni sarà sempre 180° ? È qui che la cosa si fa incredibile. In qualunque triangolo, in qualsiasi parte del mondo, la somma degli angoli interni sarà sempre 180°. Non devi credere a me. La cosa migliore da fare è sperimentare. Se ne hai voglia ti serviranno un foglio di carta, meglio a quadri (ma anche bianco o a righe andranno bene lo stesso), una matita, un righello e un goniometro.
Bene, adesso traccia tre punti a piacere, dove vuoi e uniscili con il righello. Un esempio di ciò che hai appena letto lo trovi nell’immagine animata sotto.
Una volta disegnato il tuo triangolo dobbiamo misurare gli angoli e per fare questo ci serviremo del goniometro. Se non ti ricordi come si usa il goniometro potresti leggere questo mio articolo.
Vediamo cosa succede se vado a misurare gli angoli nel triangolo che ho disegnato.
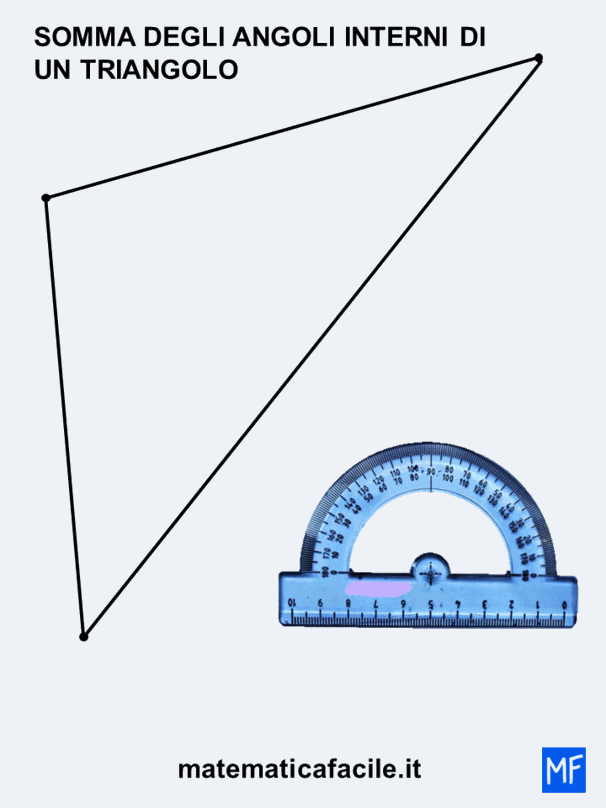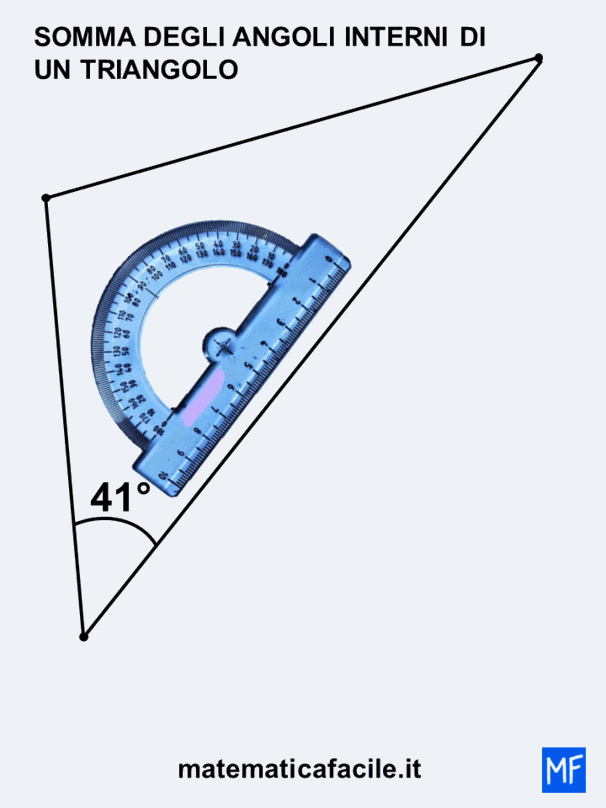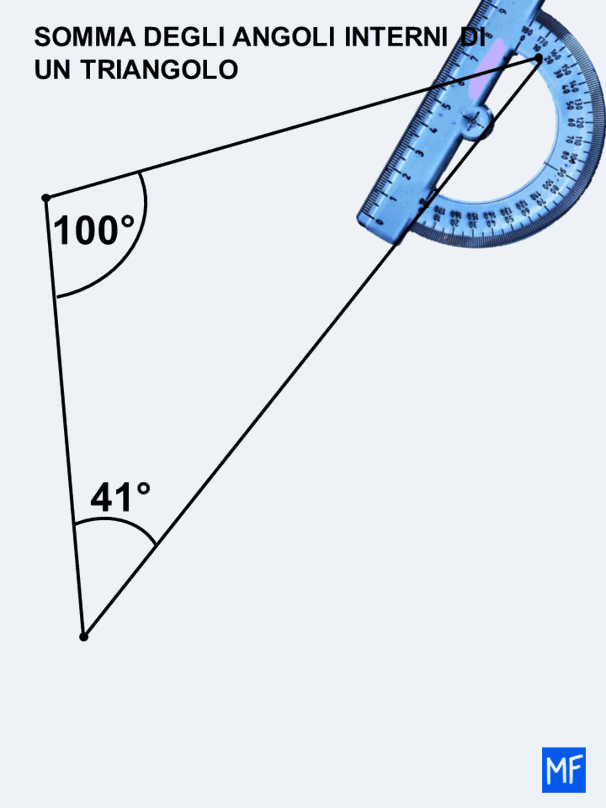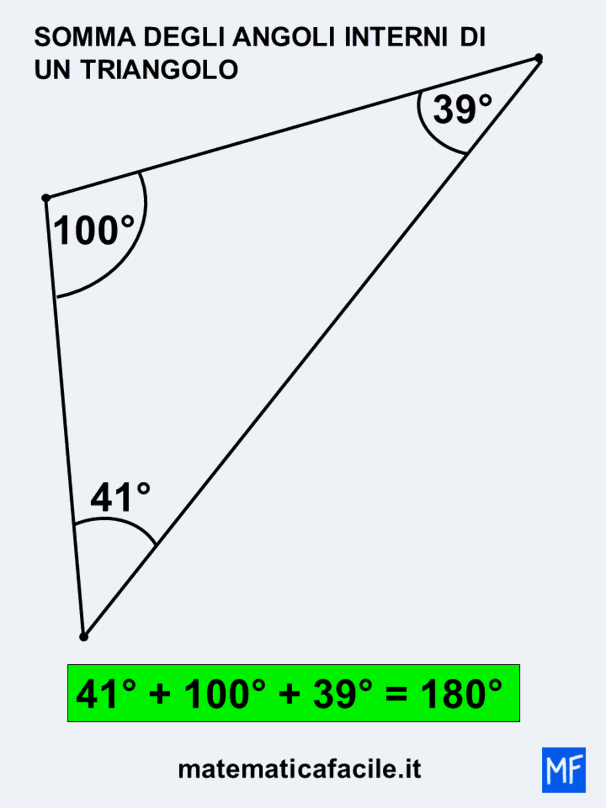
Anche in questo la somma degli interni di un triangolo è 180°. Otterrai sempre lo stesso risultato qualsiasi sia il triangolo che disegni.
esercizi
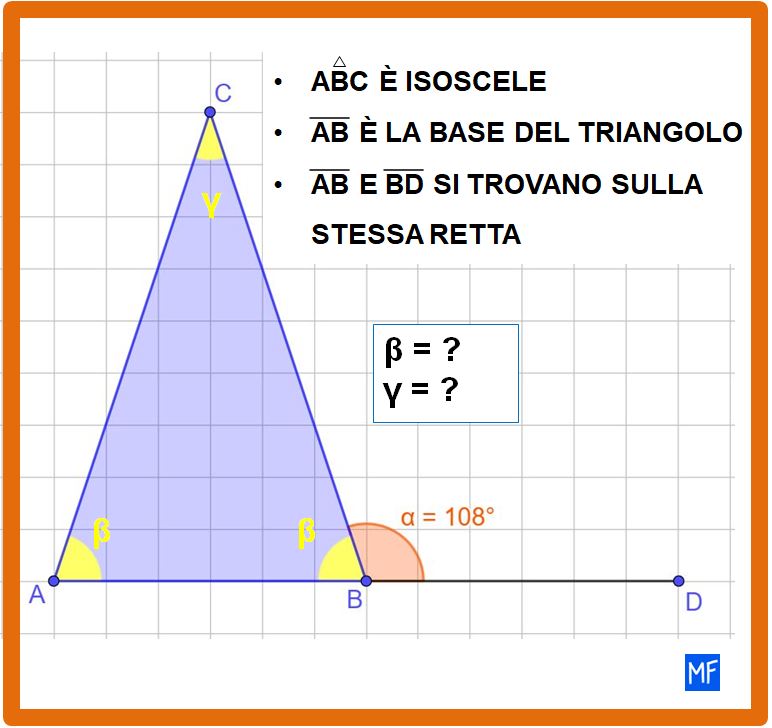
Se vuoi puoi metterti alla prova con gli esercizi che vedi nelle tre immagini sotto.
In tutti i triangoli devi calcolare l’ampiezza dell’angolo α (alfa).
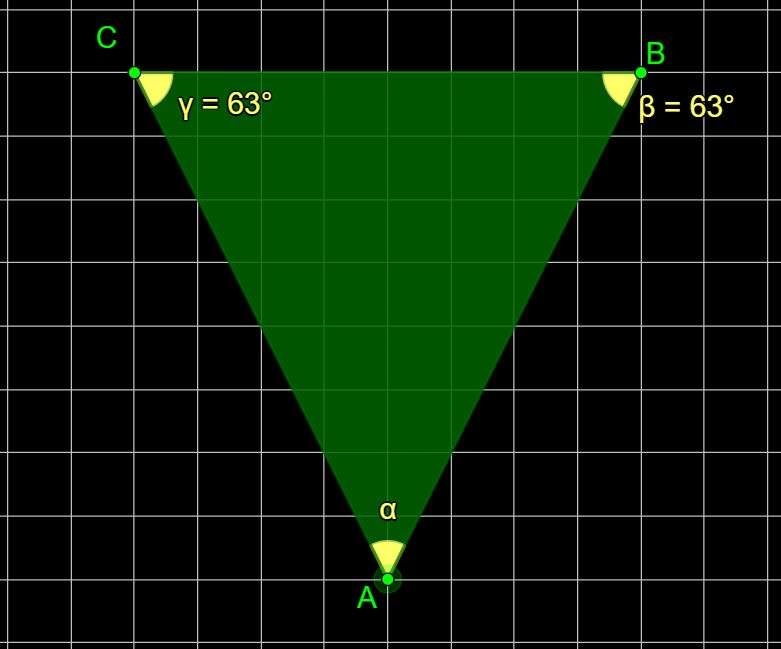
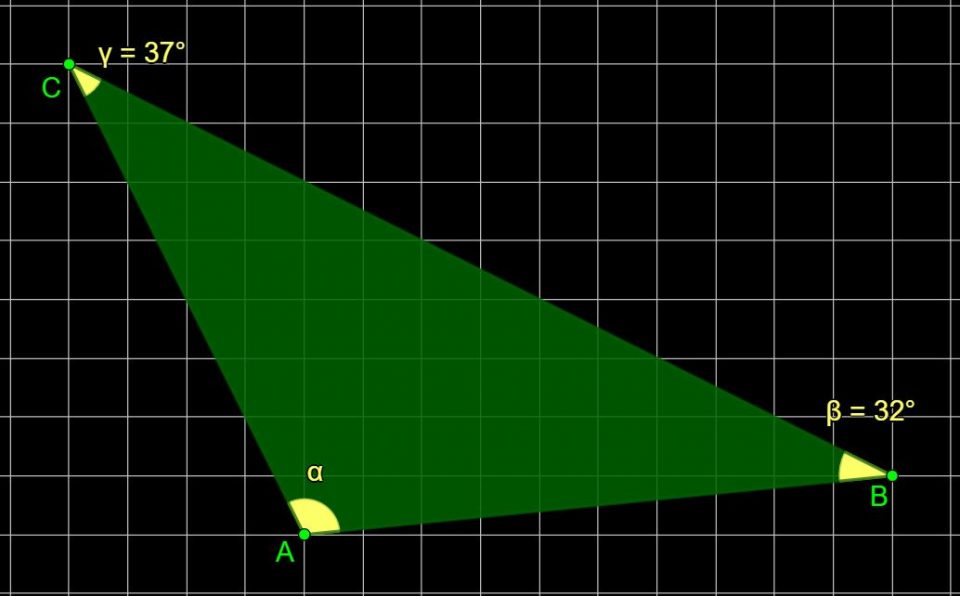
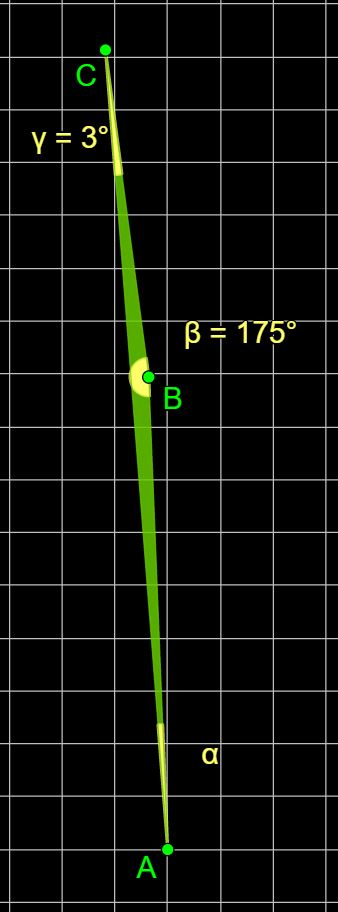
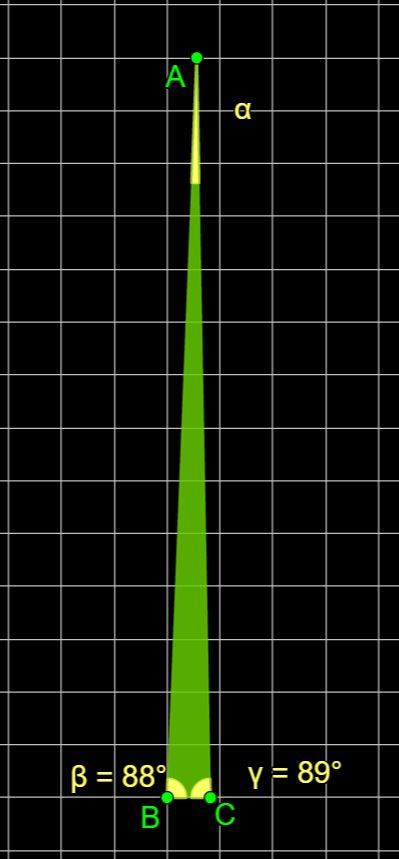
Buon lavoro.
SU youtube
link utili (spero)
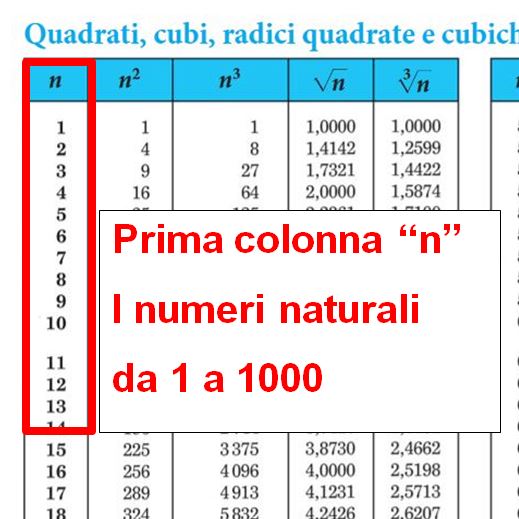
- Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe.
- Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli.
- Se vuoi ripassare l’alfabeto greco puoi visitare questa pagina.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it , saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
