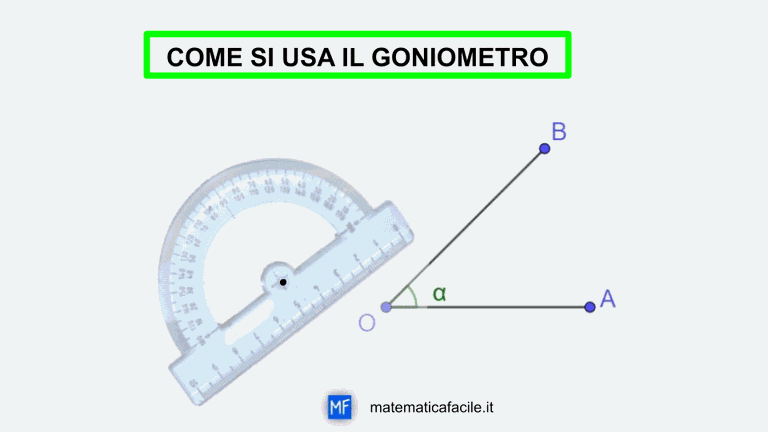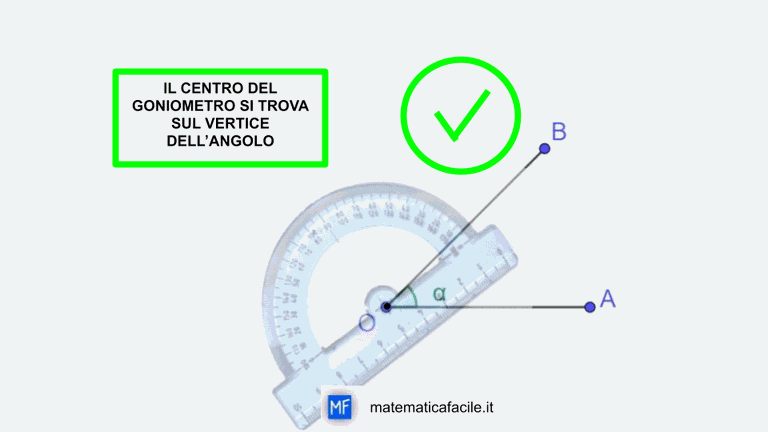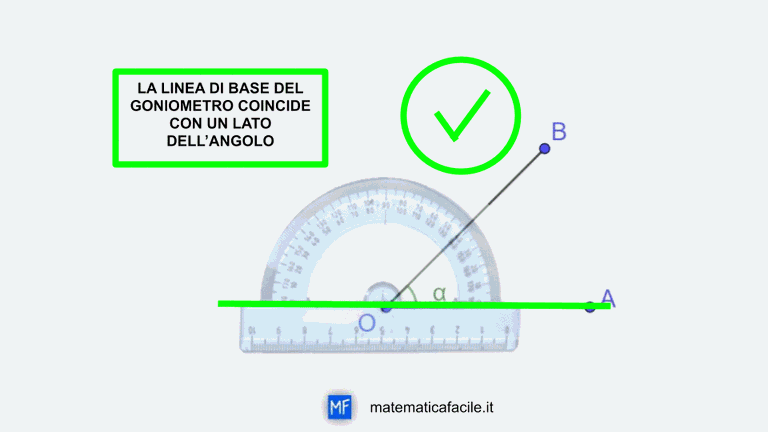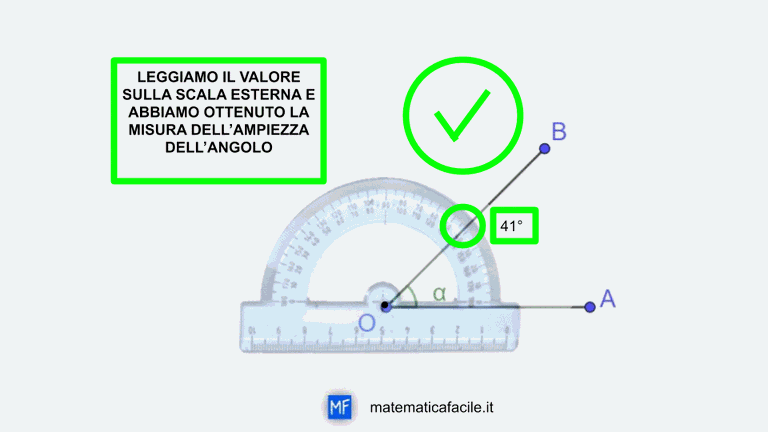
Cara mamma oggi tuo figlio ti ha chiesto di aiutarlo con gli esercizi di geometria che aveva assegnato la prof. Gli esercizi riguardano gli angoli. Per eseguire nel modo corretto la maggior parte degli esercizi con gli angoli è sufficiente un po’ di ragionamento e qualche conoscenza.
Indice
Concetti da sapere
I concetti da sapere non sono poi tanti. Vediamoli:
- Un angolo che misura 90° (si legge novanta gradi) si chiama angolo retto (i lati dell’angolo retto sono perpendicolari).
- Un angolo che misura 180° si chiama angolo piatto (i lati dell’angolo si trovano sulla stessa retta).
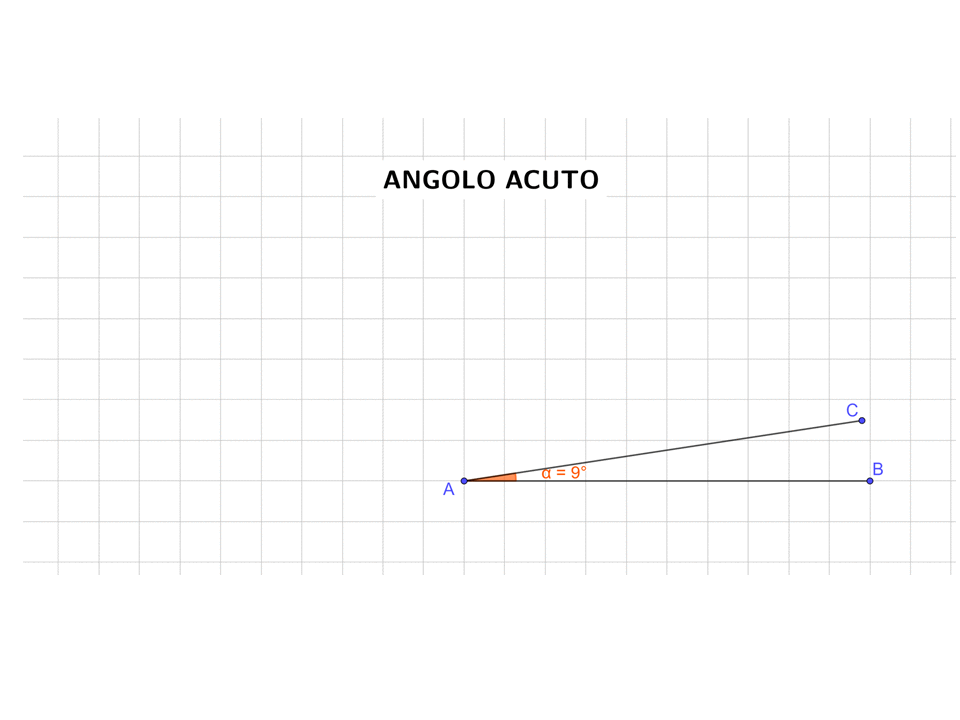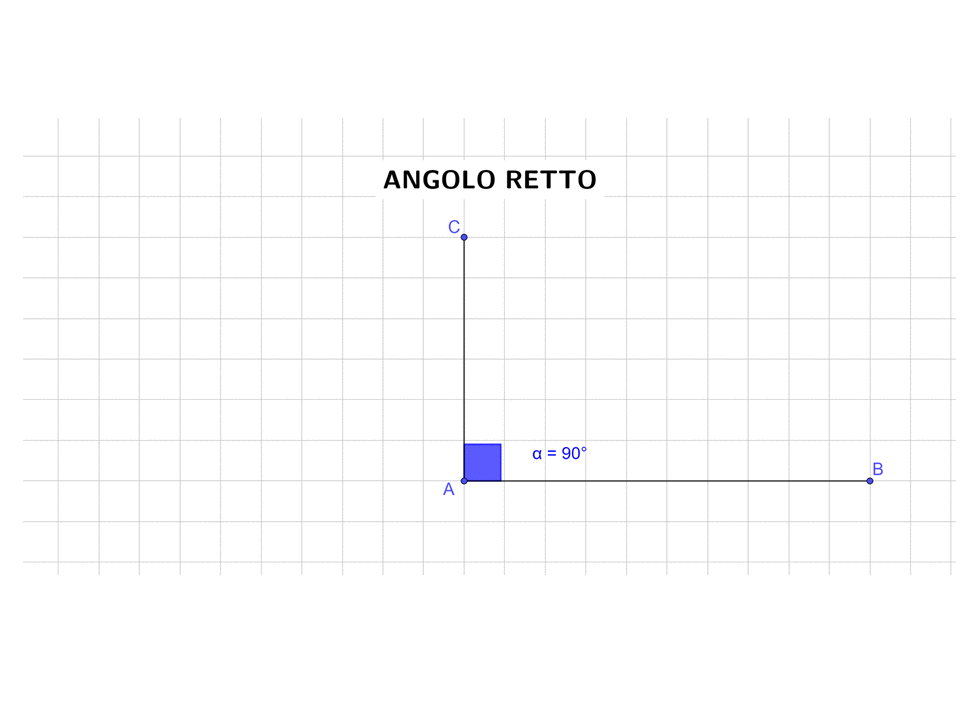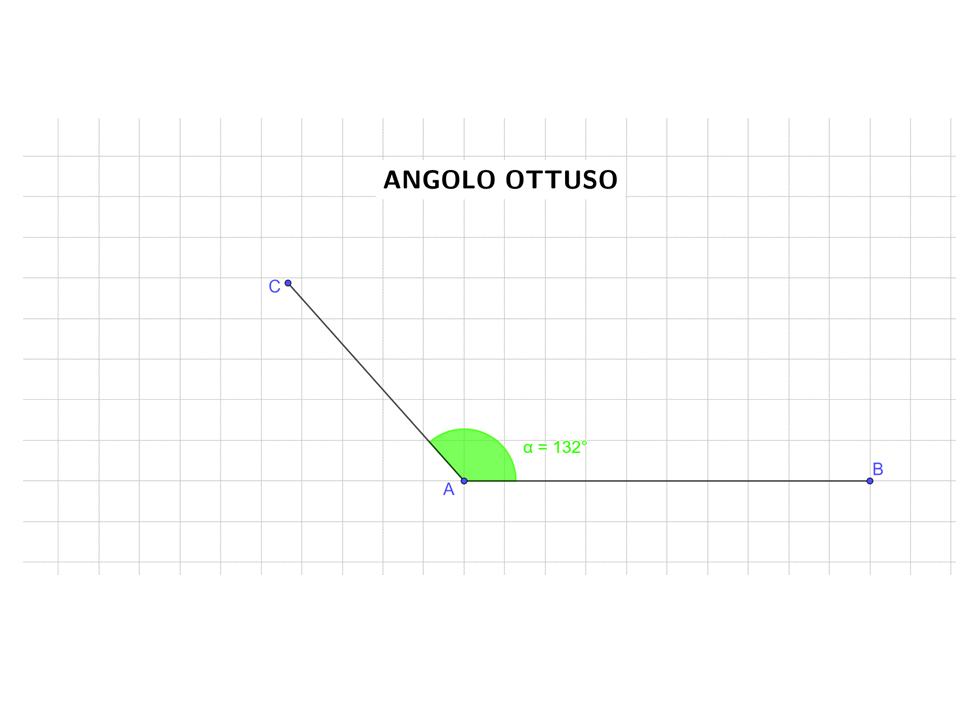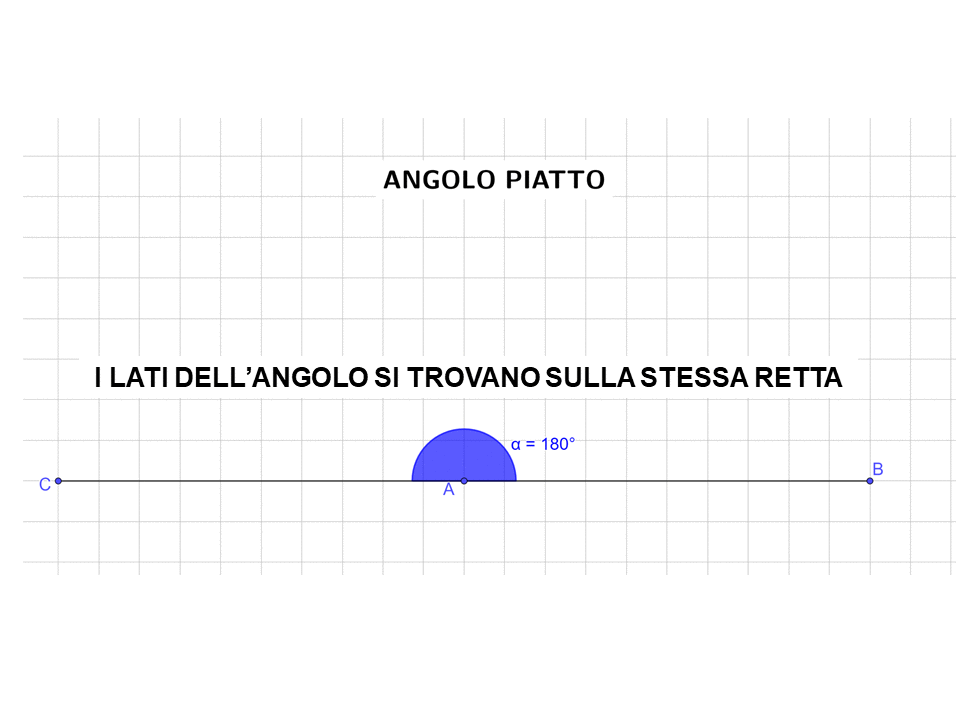
- Un angolo che è più piccolo di un angolo retto, si chiama angolo acuto.
- Un angolo che è più grande di un angolo retto, ma più piccolo di un angolo piatto, si chiama angolo ottuso.
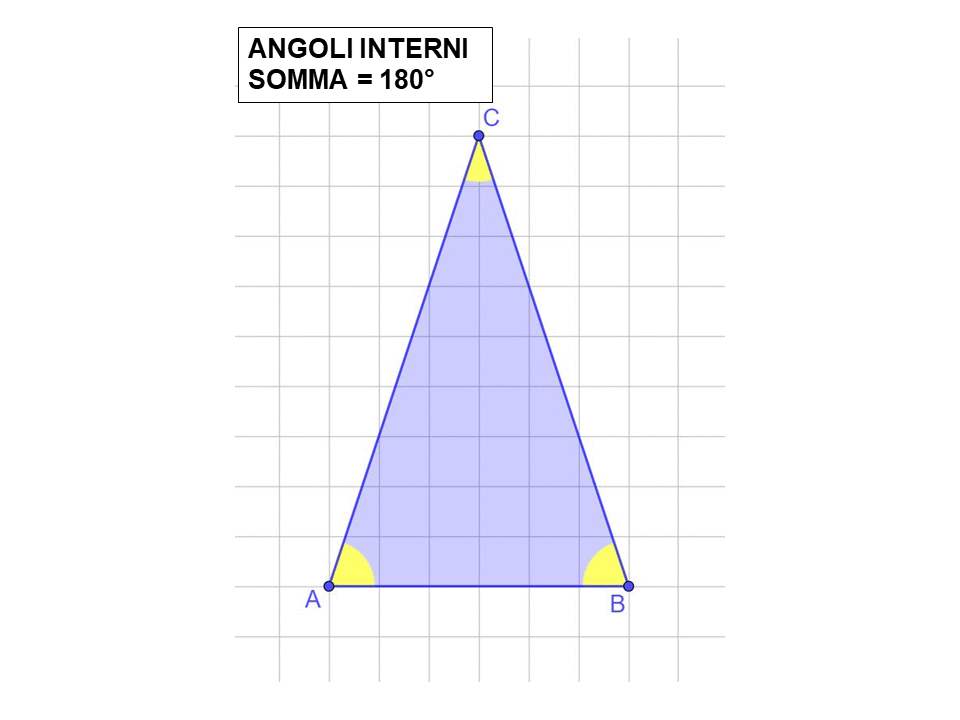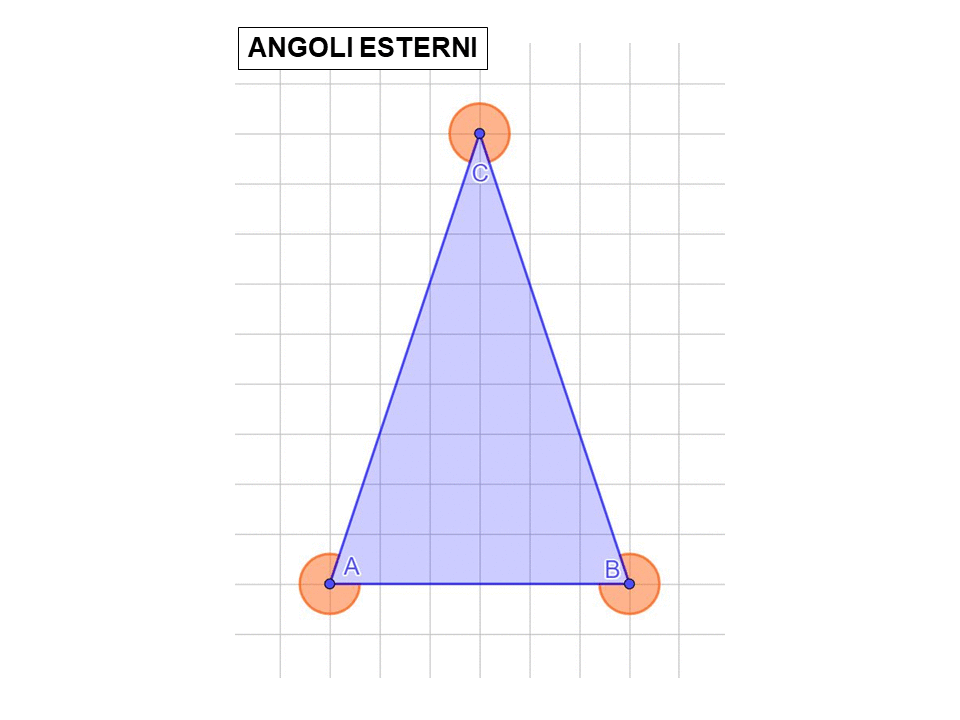
- La somma degli angoli interni di un triangolo è sempre 180°.
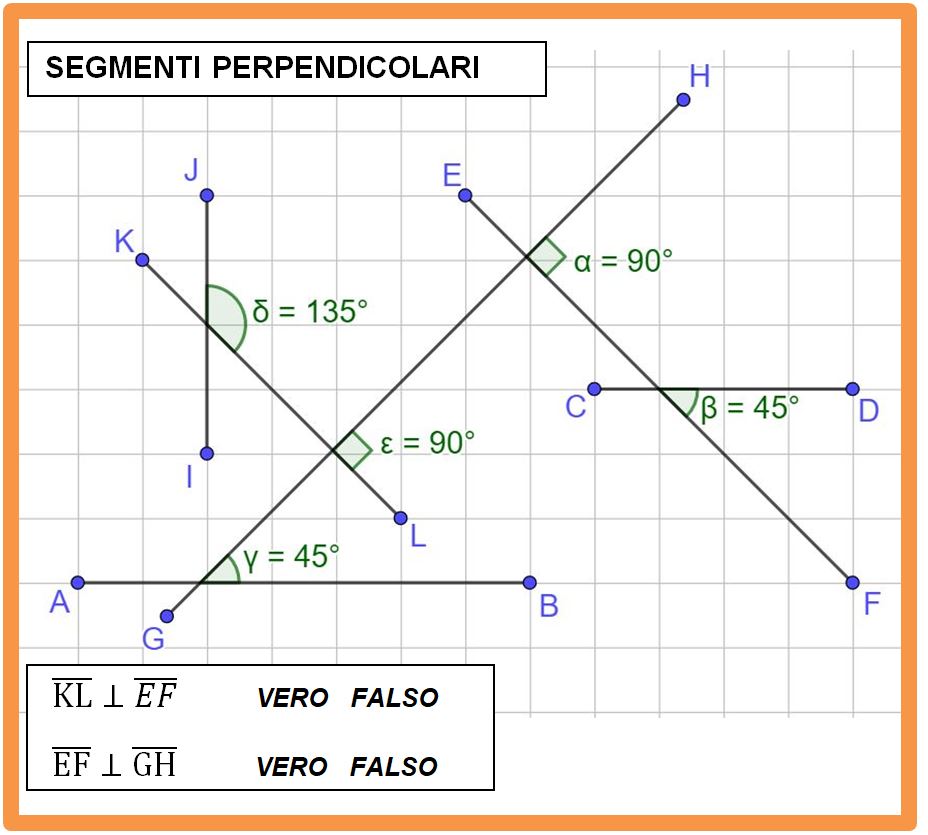
L’immagine animata sotto illustra quello che hai appena letto.
Primo esercizio
Cominciamo i nostri esercizi con gli angoli. Guardiamo bene l’immagine sotto, cerchiamo di ragionare e di rispondere alla domanda:
- Quanto misura l’angolo AÔC, cioè l’ angolo β ( si legge beta)?
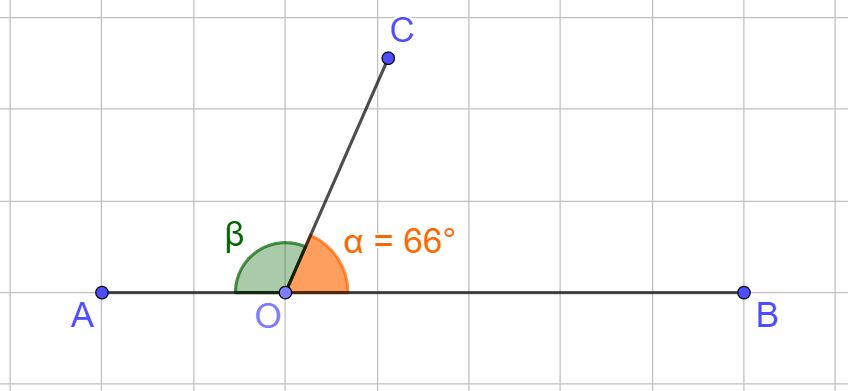
Bene, nell’immagine vediamo l’angolo α, si legge alfa, che può essere chiamato anche angolo BÔC (ti ricordo che la lettera che sta nel mezzo deve essere il vertice dell’angolo, in questo caso il punto O) che misura 66° (si legge 66 gradi).
Dobbiamo determinare l’ampiezza dell’angolo AÔC, cioè dell’ angolo β.
Cerchiamo di vedere cosa riusciamo a capire guardando l’immagine.
- Il punto O è il vertice sia dell’angolo α, sia dell’angolo β.
- Il punto O appartiene al segmento AB.
- Mi aspetto che l’angolo β sia un angolo ottuso, questo lo deduco guardando il disegno.
Osservando la figura vedo che gli archetti con cui sono disegnati gli angoli hanno dimensioni diverse, ma come ti ho già detto nel mio articolo la definizione di angolo, la grandezza dell’archetto non c’entra niente con l’ampiezza dell’angolo.
Ragionamento
L’angolo α e l’angolo β messi assieme formano un angolo piatto. Usando i numeri e i simboli, quello che abbiamo detto si scrive così:
α + β = 180°
È una semplice addizione in cui α e β sono gli addendi e 180° è la somma. Ricordando le regole che abbiamo imparato alle elementari, possiamo ricavare un addendo con una semplice sottrazione:
180° – α = β
Benissimo. Il valore dell’angolo α lo conosciamo, basta guardare il disegno, è 66°. Allora andiamo a scrivere 66° al posto di α.
180° – 66° =
Per conoscere il valore di β dobbiamo eseguire la sottrazione che leggi sopra e avremo finito.
180° – 66° = 114°
Benissimo, quindi
β = 114°
L’ angolo β quindi misura 114° (114 gradi), quindi è un angolo ottuso (perchè è più ampio di 90°), così come ci aspettavamo. Esercizio concluso.
Secondo esercizio
Continuiamo con gli esercizi con gli angoli. Ti ripeto, l’importante è imparare a ragionare, naturalmente è anche necessario conoscere qualche concetto. Lo strumento migliore per risolvere i problemi ce l’hai attaccato al collo: è la tua testa. Non avere premura quando ti trovi davanti a un problema. Prova e riprova. Non arrenderti 💪, impegnati. Vedrai che l’impegno prima o poi verrà premiato.
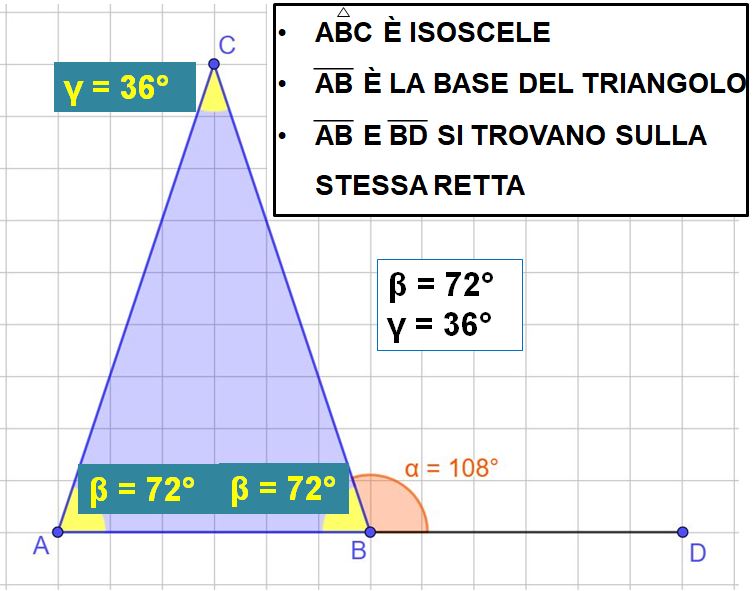
Adesso andiamo all’esercizio. Guardiamo l’immagine sotto.
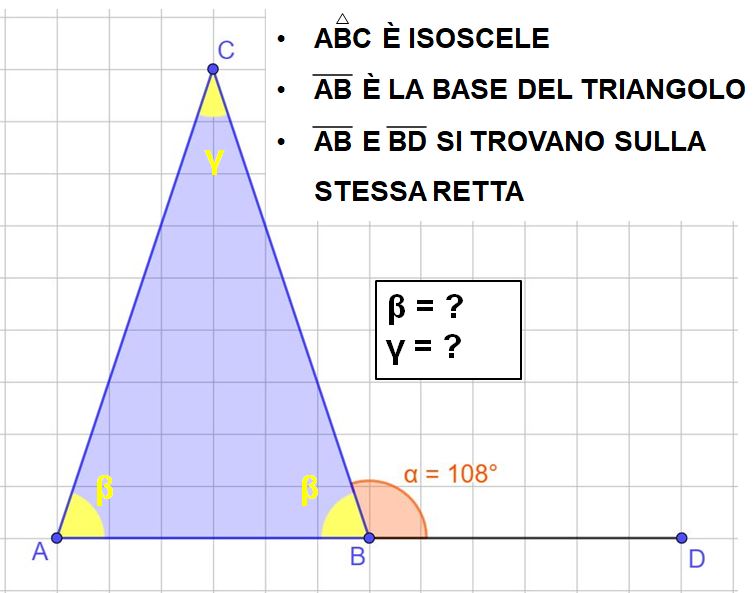
L’esercizio ci chiede di determinare le ampiezze degli angoli β e γ (beta e gamma).
Andiamo con calma. Guardiamo l’immagine e leggiamo quello che c’è scritto.
Sappiamo che il triangolo è isoscele e sappiamo anche che il lato AB è la base del triangolo. Questo vuol dire che gli angoli che sono adiacenti alla base (cioè attaccati alla base) sono uguali.
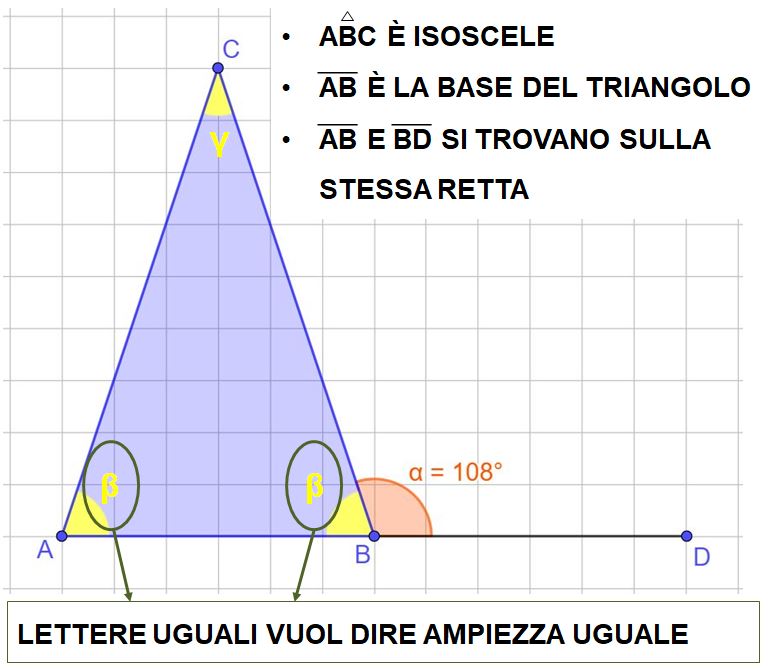
Anche se non ci ricordiamo che gli angoli alla base di un triangolo isoscele sono uguali, ci viene in aiuto l’immagine, infatti tutti e due gli angoli sono chiamati β, questo vuol dire che sono uguali, altrimenti avrebbero avuto nomi diversi.
Molto bene, con lo stesso ragionamento usato nel primo esercizio, possiamo ricavare l’ampiezza dell’angolo alla base ABC.
α + β = 180° quindi
β = 180° – α , cioè
β = 180° – 108°
eseguiamo la differenza e otteniamo
β = 72°
Fantastico. Abbiamo determinato l’ampiezza dell’angolo β. Andiamo avanti.
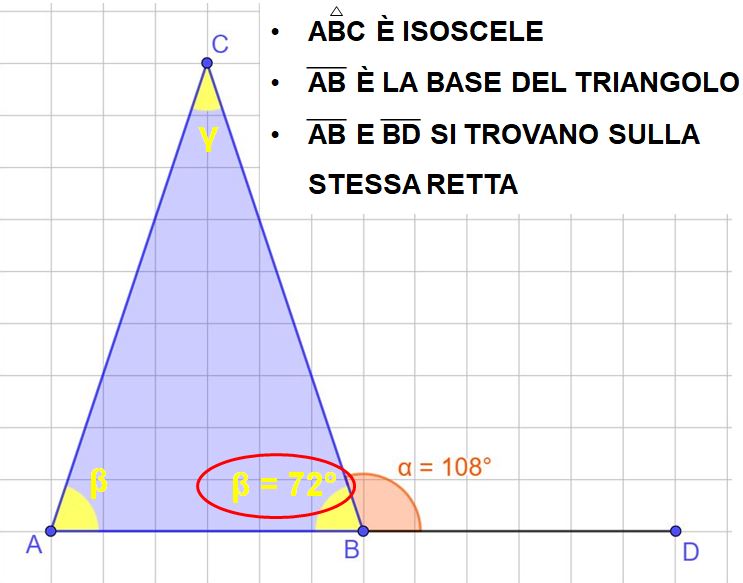
Abbiamo ricavato l’ampiezza di uno degli angoli alla base. Ma il nostro triangolo è isoscele. Questo vuol dire che i due angoli alla base sono uguali. Per cui anche l’angolo BÂC misura 72°.
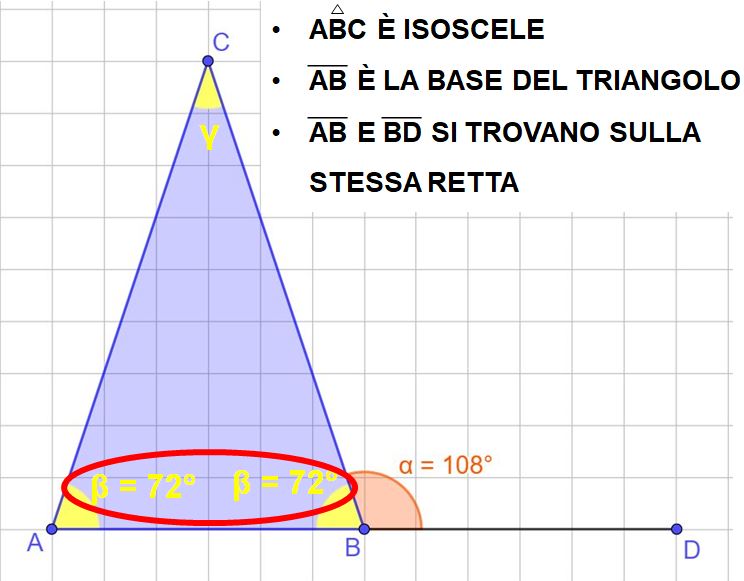
Adesso sappiamo le ampiezze dei due angoli alla base. Non ci resta che determinare l’ampiezza dell’angolo γ (gamma).
Per determinare l’ampiezza di γ dobbiamo ricordarci della regola che dice:
la somma degli angoli interni di un triangolo è 180°.
Solo per essere sicuri di ricordare la differenza tra angoli interni e angoli esterni guardiamo l’immagine sotto.
Abbiamo appena detto che la somma delle ampiezze degli angoli interni deve dare 180°. Scriviamolo usando il linguaggio matematico, cioè usando simboli e numeri:
β + β + γ = 180°
Conosciamo il valore di β, quindi possiamo ricavare l’ampiezza di γ con la sottrazione:
γ = 180° – β – β
al posto di β scriviamo il valore 72°
γ = 180° – 72° – 72°
eseguendo la sottrazione otteniamo
γ = 36°
Perfetto. Abbiamo concluso, abbiamo trovato quello che la consegna ci chiedeva. Spesso per risolvere gli esercizi sono possibili più procedimenti. L’importante è che il ragionamento seguito sia concettualmente e geometricamente corretto.
Buon lavoro.
Esercizi in pdf
Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Nel primo file sono contenute anche le soluzioni.
Lavora con calma, leggi bene le consegne e ragiona. I risultati ti servono per capire se hai lavorato bene oppure no 😉.
![]() Soluzioni Esercizi con angoli 2.pdf
Soluzioni Esercizi con angoli 2.pdf
Buon lavoro.
Link utili
- Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe.
- Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli.
- Se vuoi ripassare l’alfabeto greco puoi visitare questa pagina.
Hai dei dubbi o vuoi segnalare un errore? Puoi scivere alla casella mail: matematica.facile@libero.it , sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.