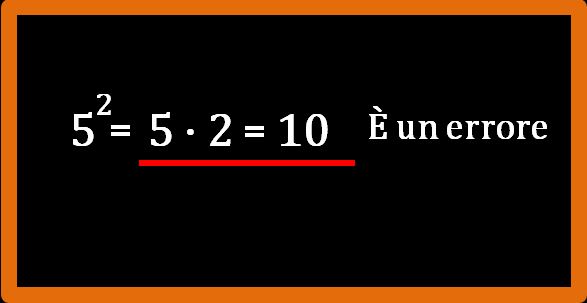
Cominciamo gli esercizi con l’elevamento a potenza con uno degli errori più comuni che gli studenti commettono.
52 = 10
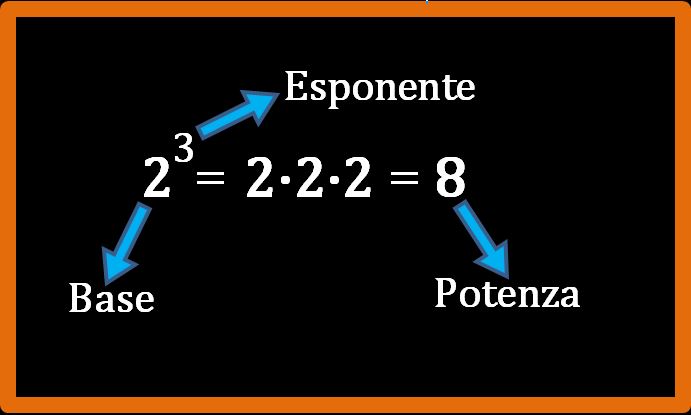
Se lavoriamo di fretta e senza riflettere, sbagliare è quasi inevitabile (non vale solo per la matematica). Nell’elevamento a potenza 52 (si può leggere 5 alla seconda oppure 5 elevato alla seconda oppure 5 al quadrato) viene naturale moltiplicare la base (5) per l’esponente (2).
Se non ti ricordi cosa sono base ed esponente, puoi dare un’occhiata a questo mio articolo. Vediamo quale è il procedimento corretto da seguire e a quale risultato ci porta.
E se non l’hai ancora fatto, iscriviti al mio canale Youtube.
Indice
Primo esercizio
Dobbiamo ricordarci a cosa servono le potenze: ‘Le potenze servono per scrivere in modo veloce una moltiplicazione in cui i fattori sono tutti uguali ‘. (Ti ricordo che i fattori sono gli elementi della moltiplicazione). Nella moltiplicazione
5 · 2
I fattori non sono uguali, infatti il primo fattore è il numero 5, invece il secondo fattore è il numero 2.
Il procedimento corretto da seguire è questo: si deve scrivere una moltiplicazione in cui i fattori sono tutti uguali alla base e vanno ripetuti tante volte quante indicato dall’esponente. Dirlo a parole è molto più complicato che scriverlo con i numeri:
Nei primi esercizi è meglio eseguire tutti i passaggi, anche se è necessario un po’ di tempo in più. Impiegare cinque minuti in più adesso ti farà risparmiare ore nei prossimi esercizi (e ti permetterà di prendere un buon voto nella verifica).
Guardiamo quello che c’è scritto nella lavagna.
Ripetiamo: scrivere 52 vuol dire eseguire una moltiplicazione in cui la base (5) si ripete due volte (il numero indicato dall’esponente, cioè 2).
Il risultato dell’elevamento a potenza allora è:
Secondo esercizio
Continuiamo con altri esercizi con l’elevamento a potenza.
Eseguiamo 6 alla seconda (oppure 6 al quadrato, quando l’esponente è 2 si può anche dire che la base è elevata al quadrato). Cominciamo con scrivere il segno della moltiplicazione.
Molto bene. Ora scriviamo i fattori della moltiplicazione che devono essere tutti uguali tra loro, ma devono anche essere uguali alla base, che nel nostro esempio è 6.
Fantastico. Ora ci dobbiamo chiedere: quante volte si deve ripetere il fattore 6? Andiamo a guardare l’esponente. L’esponente è 2, vuol dire che il fattore 6 va ripetuto due volte.
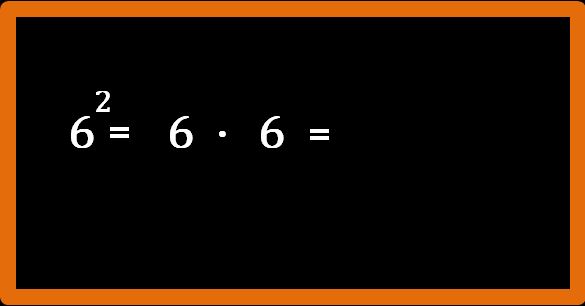
Benissimo. Abbiamo quasi finito, non ci resta che eseguire la moltiplicazione (tabellina del 6).
Terzo esercizio
Ancora un altro esercizio con l’elevamento a potenza. Questa volta cerchiamo di andare un po’ più veloci.
Eseguiamo il seguente elevamento a potenza 7 alla terza oppure 7 al cubo, quando l’esponente è 3 si può anche dire che la base è elevata al cubo :
Abbiamo imparato che quello che dobbiamo fare è scrivere una moltiplicazione come quella sotto:
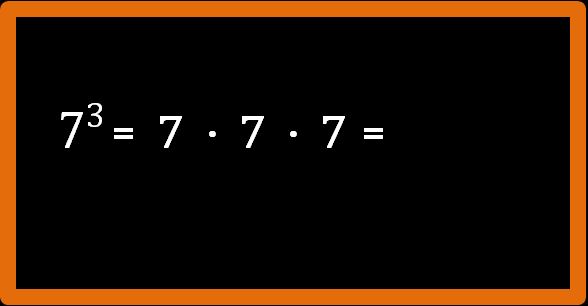
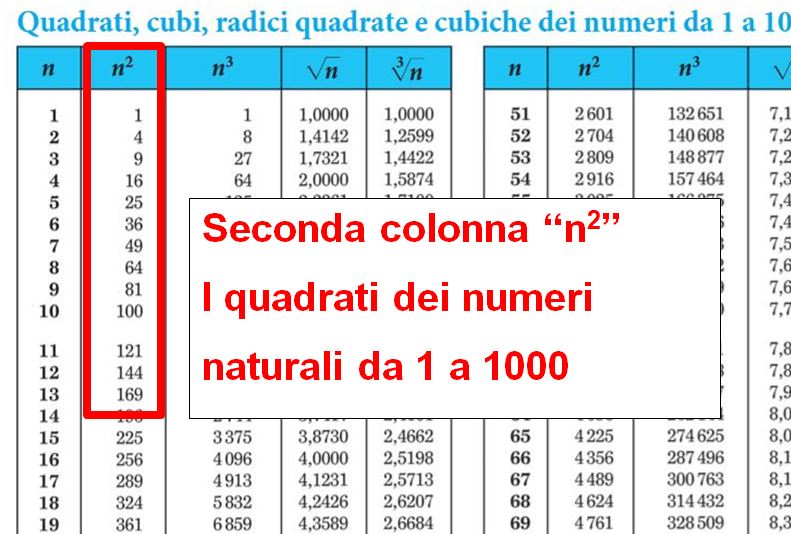
La base (7) si deve ripetere tre volte (perchè l’esponente è 3). Non ci rimane che eseguire la moltiplicazione oppure possiamo consultare le tavole numeriche.
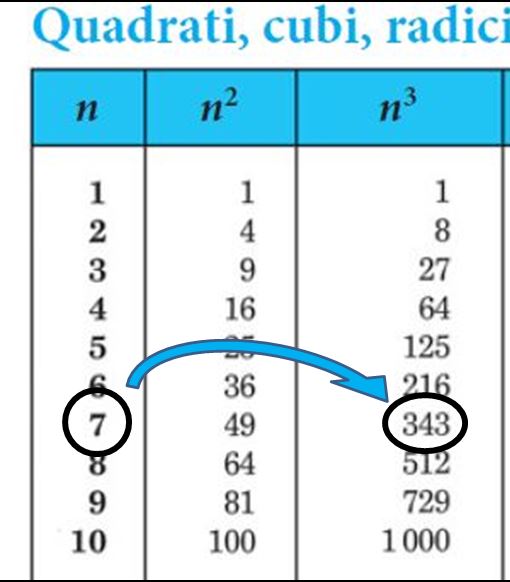
Il risultato che stavamo cercando è 343. Esercizio concluso.
Esercizi in pdf
Adesso possiedi tutti gli strumenti necessari per eseguire in modo corretto qualsiasi elevamento a potenza. Se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Puoi consultarli o se preferisci scaricarli e stamparli. Lavora con calma, leggi bene la consegna e non ti preoccupare se sbagli, nessuno verrà a rimproverarti.
ELEVAMENTO A POTENZA – ESERCIZI.pdf
ELEVAMENTO A POTENZA_ESERCIZI – SOLUZIONI.pdf
Buon lavoro.
Link utili
Nelle tavole numeriche puoi trovare i numeri da 1 a 1000 elevati alla seconda e alla terza. Se hai perso le tavole o se nel tuo libro non le hai trovate, puoi consultarle o scaricarle da questa pagina della Casa Editrice Zanichelli.
Se hai dubbi o vuoi segnalare un errore puoi lasciare un commento oppure puoi scrivere alla casella mail: matematica.facile@libero.it , sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.
