L’ angolo è una parte di piano compresa tra due semirette che hanno la stessa origine. Questa è la definizione di angolo che ho trovato in quasi tutti i libri di geometria che ho avuto modo di leggere.
Se cerchi in internet trovi definizioni molto simili. Per esempio in questo link trovi la definizione di angolo, data in un libro per le scuole superiori.
Ma in una delle prime lezioni di geometria la prof ti ha spiegato che:
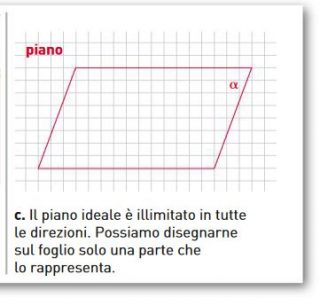
il piano è una superficie piana che si estende in tutte le direzioni all’infinito.
Anche in questo caso se cerchi in internet la definizione di piano è più o meno sempre la stessa, come puoi vedere nell’immagine sotto.
Indice
- Una domanda interessante
- L’angolo definito da Euclide
- Il ciclista e la leggera salita
- Il ciclista e la salita faticosa
- L’angolo come inclinazione
- La grandezza dell’archetto è importante?
- L’angolo di 90°
- In sintes6
- Esercizi in pdf
- Esercizio si Youtube
- Iscriviti al nostro canale YouTube → matematicafacile
Una domanda interessante
Questi concetti si imparano e si accettano come veri senza riflettere. Lo ha detto la prof, è scritto nel libro quindi sarà sicuramente così. Alcune persone però ci hanno riflettuto sopra e si sono chieste:
Il piano è infinito, allora anche una sua parte è infinita. Quindi l’angolo, che è una parte di piano, è infinito. Ma se è infinito come facciamo a misurarlo? Quando usiamo il goniometro cosa stiamo misurando?
La domanda è lecita. Forse l’immagine animata ci può aiutare a capire meglio la situazione.

Il problema sta proprio nella definizione di angolo. Dato che con il goniometro possiamo misurare gli angoli si dovrebbe cercare una definizione più appropriata.
L’angolo definito da Euclide
La definizione di angolo che io preferisco è quella data da Euclide, un matematico vissuto in Grecia circa 2300 anni fa.

Il signore che vedi nell’immagine è Euclide. In realtà non sappiamo se l’immagine sia somigliante a come era Euclide nella realtà, ma è così che oggi tutti lo immaginano. Euclide è considerato il padre della geometria perchè ha scritto un’ opera che si chiama Elementi che dopo più di 2000 anni è ancora molto venduta. Secondo alcune stime è tra i primi libri per numero di edizioni e ristampe al mondo. Se fosse ancora vivo si sarebbe arricchito grazie al suo libro. Negli Elementi Euclide racchiude, tra le altre cose, tutto il sapere dell’epoca che riguardava la geometria. È per questo motivo che la geometria che studiamo a scuola si chiama Geometria euclidea.

Ma quale definizione dà Euclide per l’angolo?
Euclide scrive più o meno così:
“Un angolo è l’inclinazione di una linea rispetto a un’altra”
Dato che Euclide lo ha scritto in greco, le traduzioni possono essere un po’ differenti l’una dall’altra, ma la sostanza della frase è sempre la stessa ed è abbastanza chiara.
Il ciclista e la leggera salita
Il concetto di inclinazione è abbastanza semplice da immaginare e da capire. Aiutiamoci prendendo come esempio un ciclista che percorre una strada. Inoltre l’inclinazione è una grandezza che si può misurare.

Nell’immagine animata che vedi sopra il ciclista prima percorre una strada pianeggiante e poi una strada in leggera salita. Più precisamente la strada in salita ha una inclinazione di 10°. L’inclinazione viene misurata prendendo come riferimento la continuazione delle strada pianeggiante, che è indicata con una linea tratteggiata.
Vediamo cosa succede se l’inclinazione della strada aumenta.
Il ciclista e la salita faticosa
Se l’inclinazione della strada aumenta, la salita si fa più ripida e più difficile da scalare. Come spesso hai visto (o fatto) i ciclisti nelle salite più difficoltose si alzano sui pedali per avere una spinta maggiore. Quindi inclinazione maggiore, vuol dire angolo maggiore.

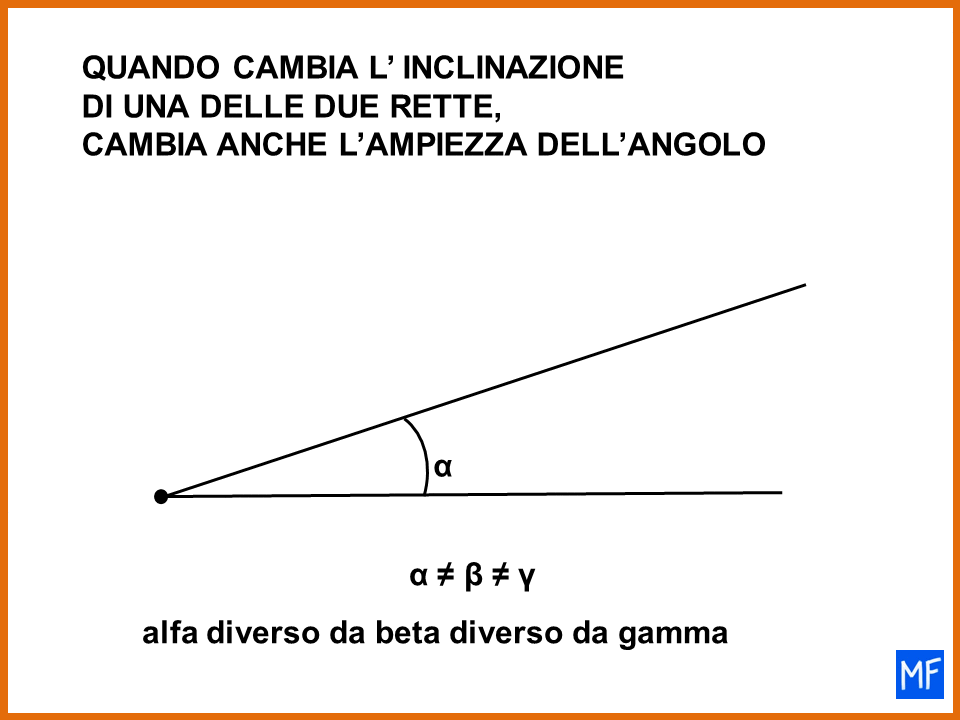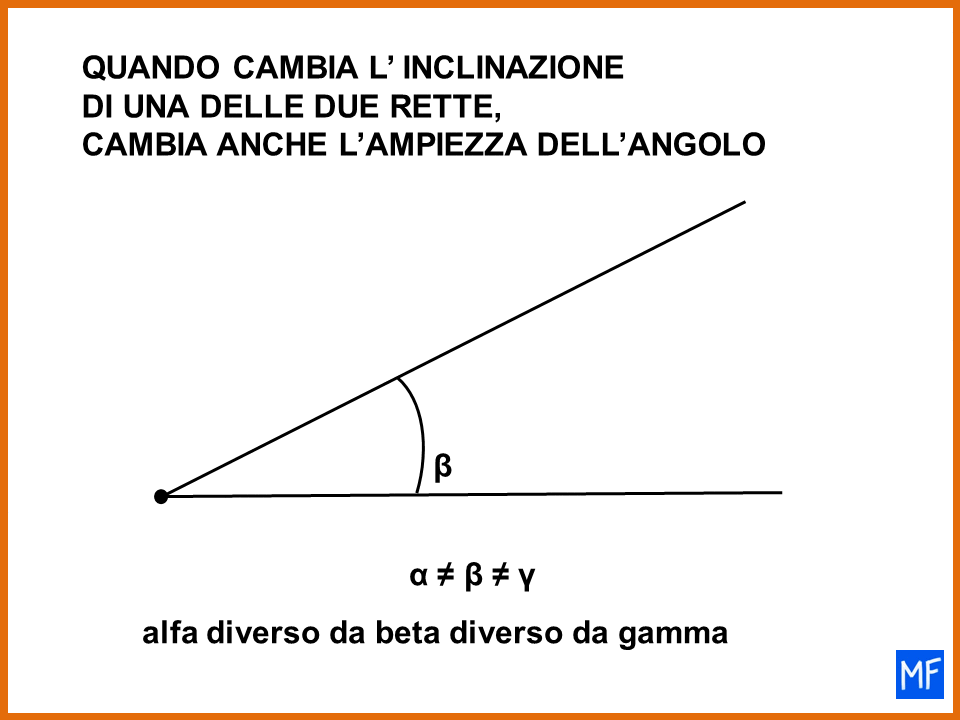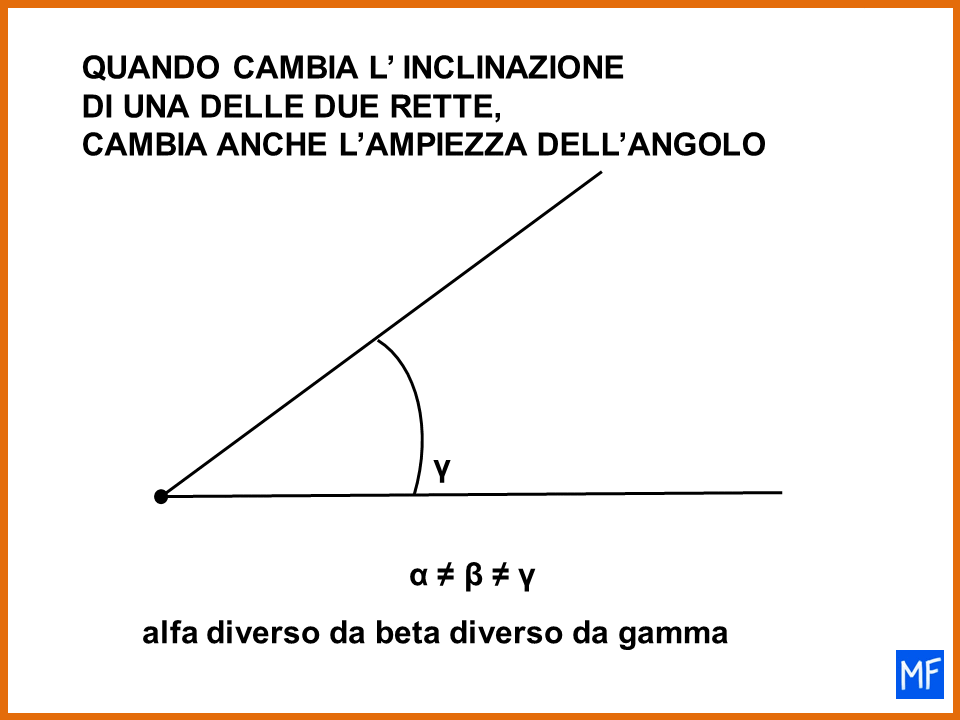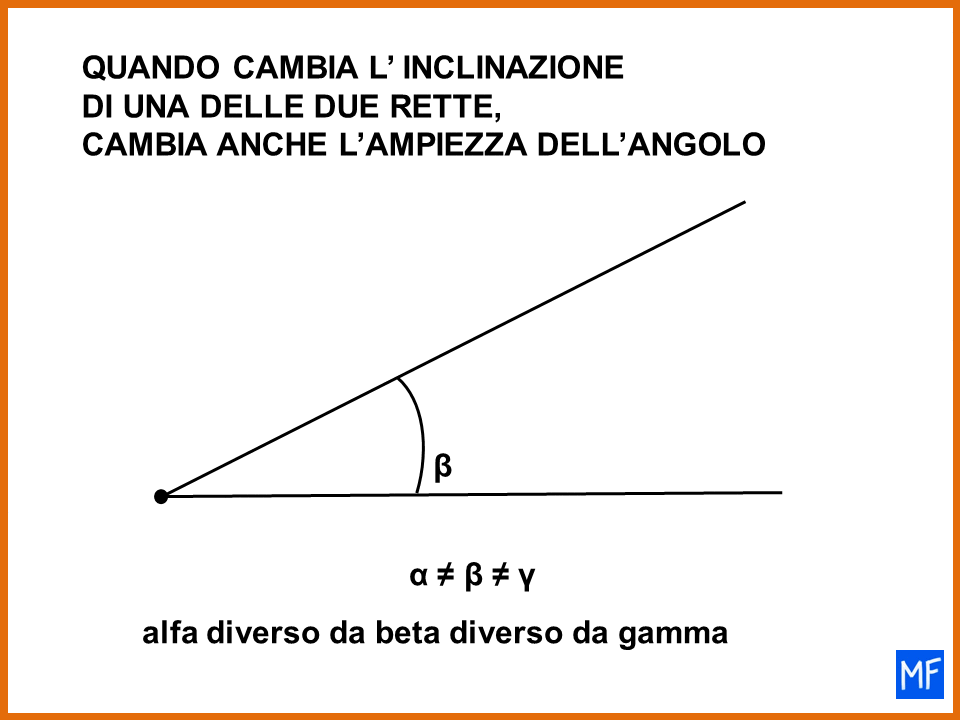
L’angolo come inclinazione
Da questi esempi emerge che forse la definizione di angolo come inclinazione di una retta rispetto a un’altra potrebbe risultare più appropriata. Per quanto mi riguarda è quella che preferisco.
Nell’esempio della strada, il vertice dell’angolo è il punto in cui si passa dalla pianura alla salita.
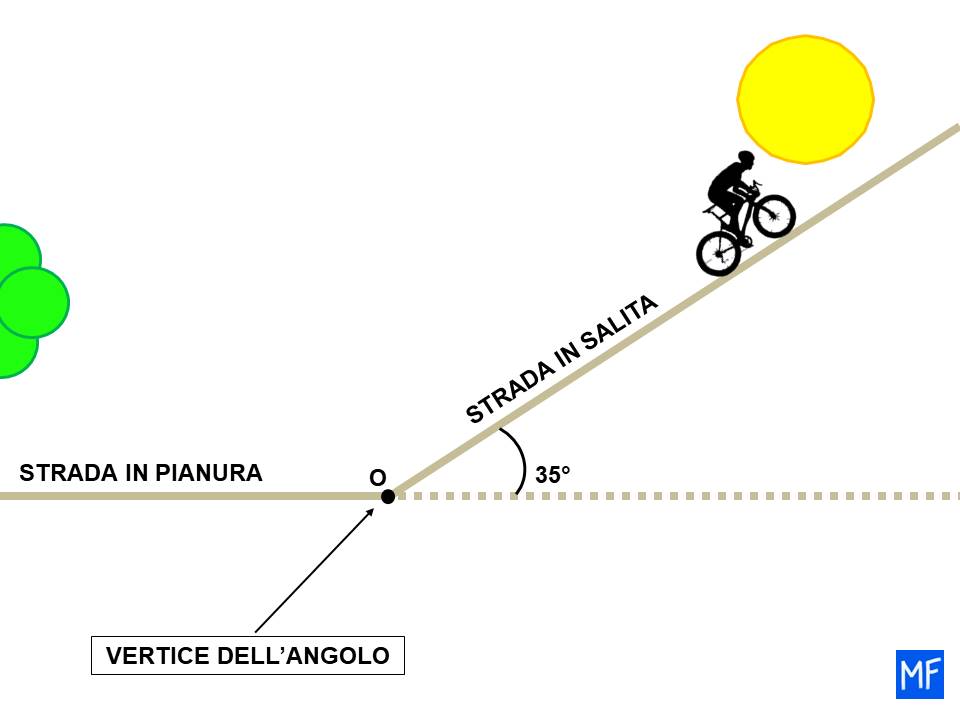
I lati dell’angolo sono dati dalla strada in salita e dalla immaginaria continuazione della strada in pianura, che nell’immagine sopra è indicata con il tratteggio.
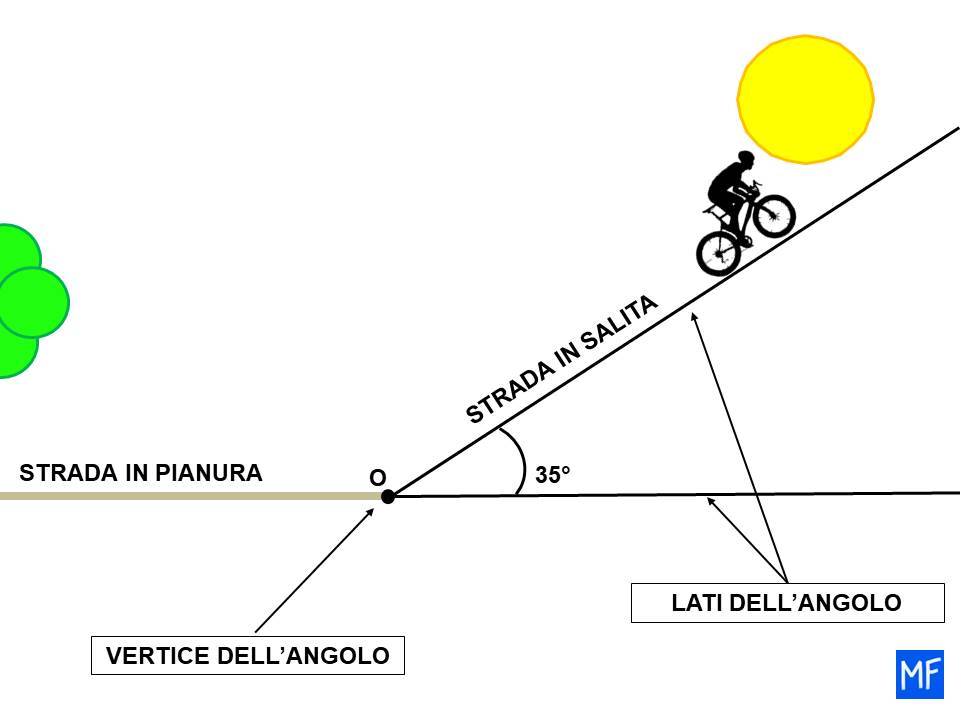
Risulta facile capire che più grande è l’angolo, più ripida è la salita.
Detto in un altro modo: maggiore è l’ampiezza dell’angolo, maggiore è l’inclinazione della strada in salita.
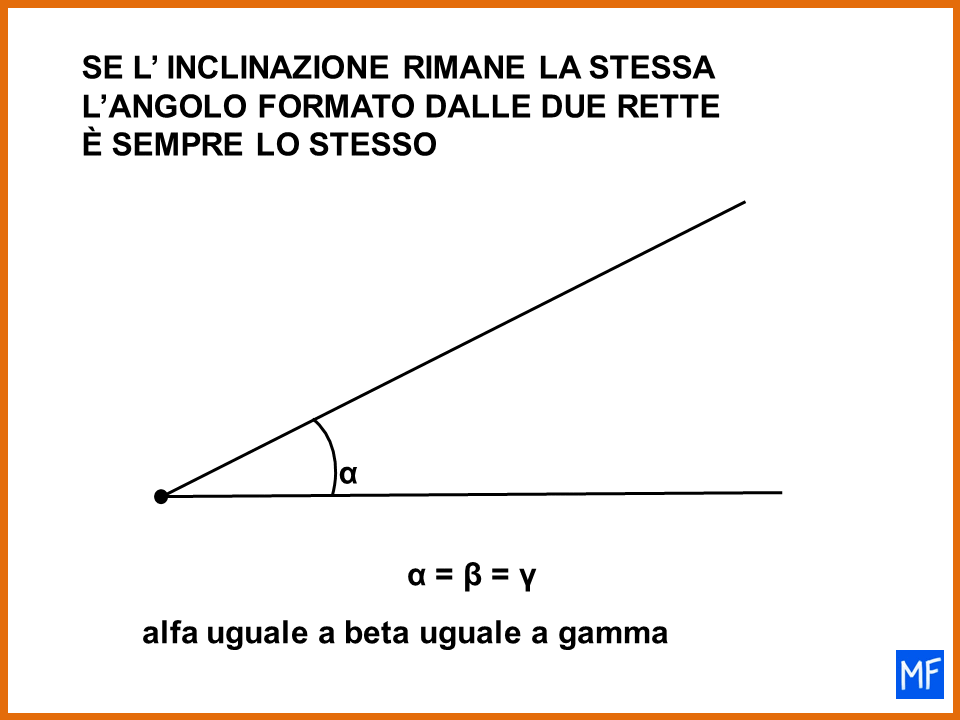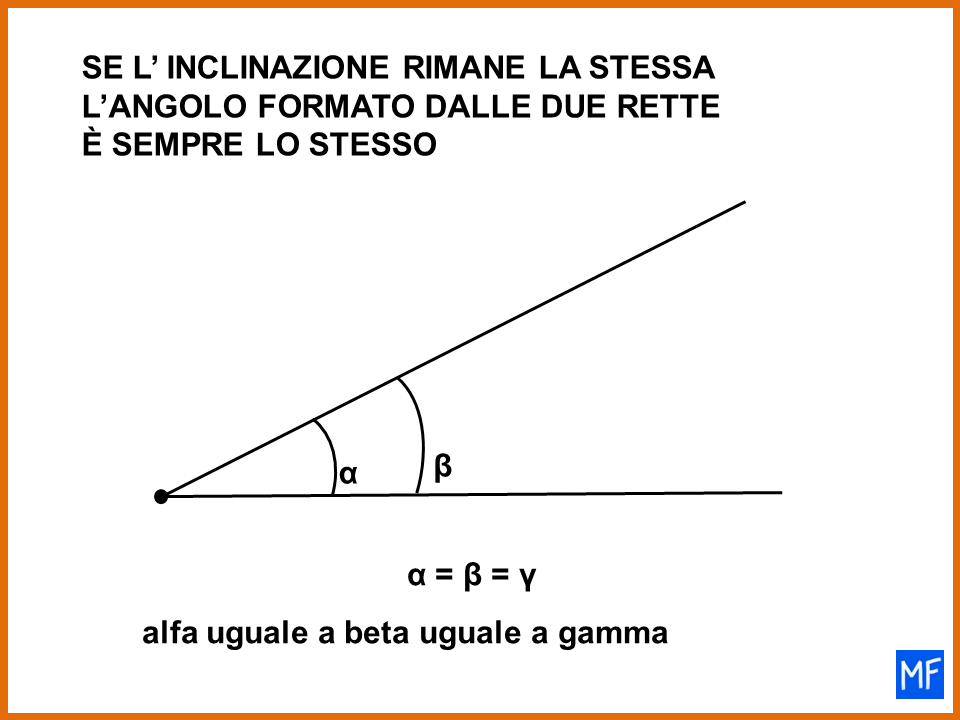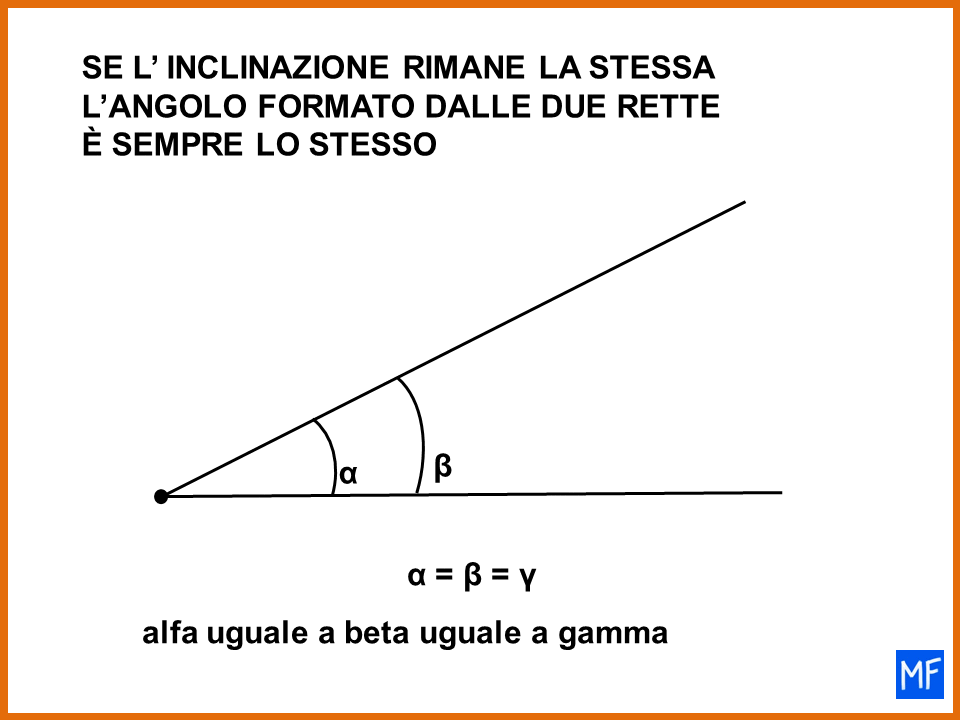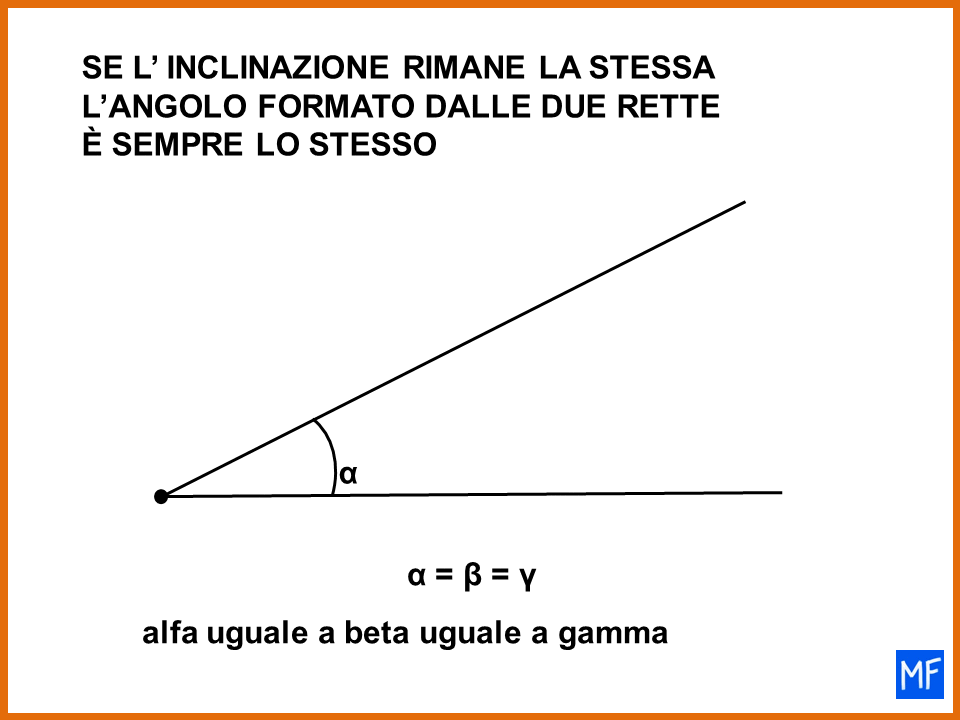
La grandezza dell’ archetto È importante?
Molto bene, dopo avere spiegato perché la definizione di angolo che preferisco è quella di Euclide, è il caso di chiarire bene un aspetto su cui molti studenti sbagliano. Guarda con attenzione l’immagine sotto e rispondi alla domanda:
- È più ampio l’angolo α oppure l’angolo β ?

Il 75% degli studenti risponde l’angolo β. È la risposta sbagliata.
In realtà i due angoli sono uguali. Hanno la stessa ampiezza.
Per rendercene conto dobbiamo ricordarci la definizione di angolo:
L’angolo è l’inclinazione di una retta rispetto a un’altra.
I due angoli (α e β) indicano tutti e due l’inclinazione della stessa strada, cioè della strada in salita.
Questo vuol dire che la grandezza dell’archetto non ha nessuna importanza. Quello che conta è l’inclinazione della retta che prendiamo in considerazione.
L’angolo di 90°
Per capire meglio quello che abbiamo appena detto, facciamo un esempio con un angolo di 90°, cioè con un angolo retto. Ti ricordo che l’angolo retto non si indica con un archetto, ma con due piccole linee dritte.
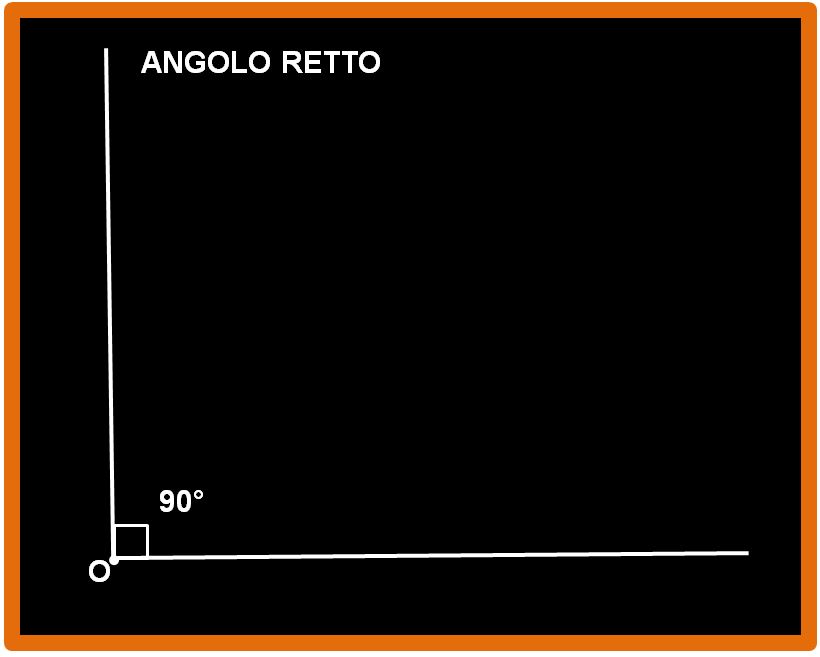
Molto bene, adesso guarda l’immagine sotto.
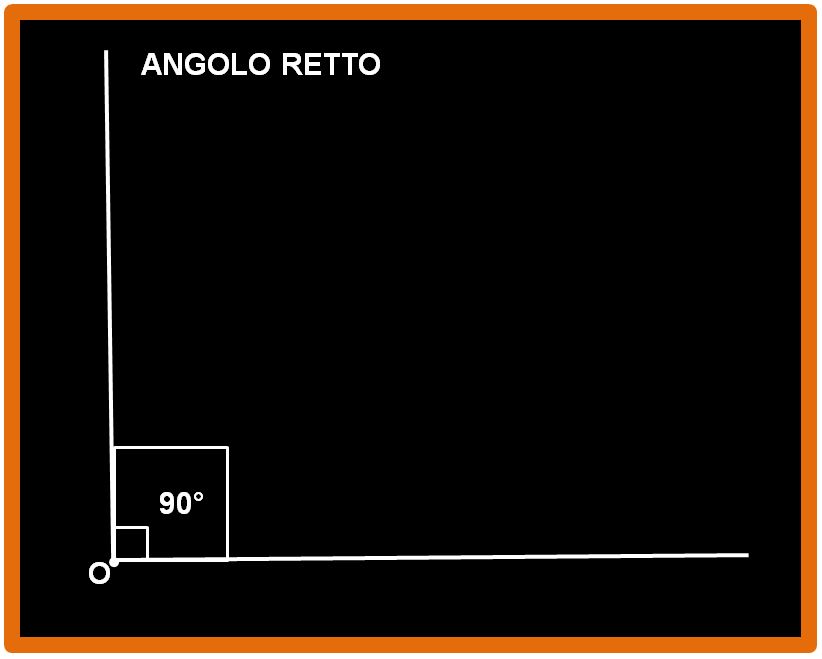
Anche se le linee usate per indicare l’angolo sono più grandi, l’angolo è sempre lo stesso. L’ampiezza dell’angolo è sempre 90°. Quello che conta è l’inclinazione reciproca delle due rette, non la dimensione dell’archetto o delle linee dritte.
In sintesi
- se cambia l’inclinazione di una delle due rette cambia anche l’ampiezza dell’angolo formato dalle due rette.
- se invece l’inclinazione delle due rette rimane la stessa, l’angolo formato dalle rette è sempre lo stesso.
Esercizi in pdf
Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Leggi con attenzione la consegna e lavora con calma.
Buon lavoro.
Su Youtube
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche. Ricorda: sapere usare le tavole numeriche può essere molto utile, infatti potrai utilizzarle anche durante le verifiche in classe. Se ti piace la chimica, invece puoi cliccare qui, si aprirà una tavola perdiodica interattiva degli elementi, sempre fornita dalla Zanichelli. Se vuoi ripassare l’alfabeto greco puoi visitare questa pagina.
Se hai dubbi o vuoi segnalare un errore puoi scivere alla casella mail: matematica.facile@libero.it , saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
In questa pagina sono presenti link di affiliazione che garantiscono a questo sito una piccola quota di ricavi, senza variazione del prezzo per l’acquirente.