Bene, hai imparato a eseguire la somma tra frazioni, poi la moltiplicazione tra frazioni e hai anche imparato come si ricava la frazione inversa di una frazione data. Ora è arrivato il momento di fare un altro passo avanti. In questo articolo parleremo di divisione tra frazioni: esempi ed esercizi.
Quello che cercheremo di capire è come si esegue una cosa del genere:
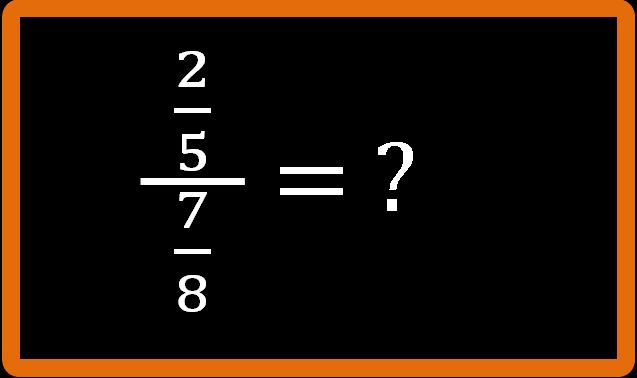
È una frazione che ha come numeratore una frazione e come denominatore un’ altra frazione. Niente paura. Con 5 minuti di impegno riuscirai a calcolare questa frazione. Vedrai che non è poi così complicato. All’inizio è normale se qualcosa non ti riesce, ma con la pratica e l’esercizio tutto diventerà più facile.
Indice
Esempio 1
Cominciamo con la nostra frazione. Come ti ho detto più volte, una frazione non è altro che una divisione scritta in un modo diverso. Quindi possiamo scrivere la frazione di partenza in questo modo:
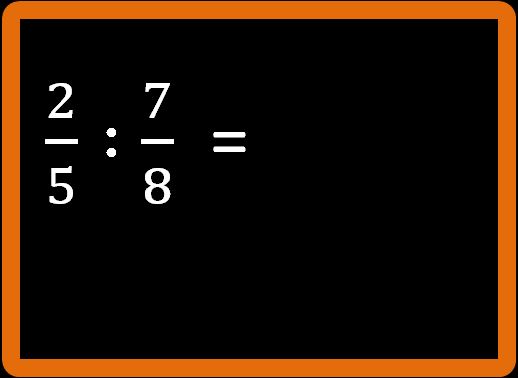
Molto bene, fin qui niente di difficile. Vediamo ora cosa dice la regola:
“Per dividere una frazione per un’altra, si riscrive la prima e si moltiplica per l’inverso della seconda”.
Facciamolo passo passo.
Riscriviamo la prima frazione:
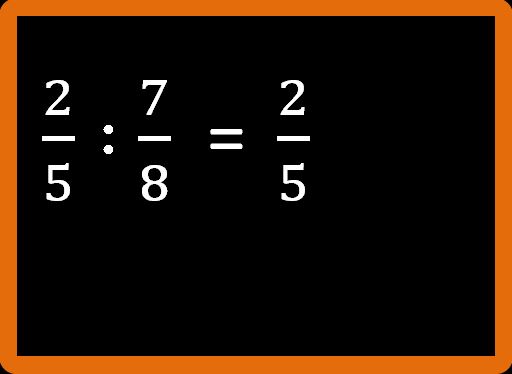
Invece del segno della divisione dobbiamo scrivere il segno della moltiplicazione: ” • “.
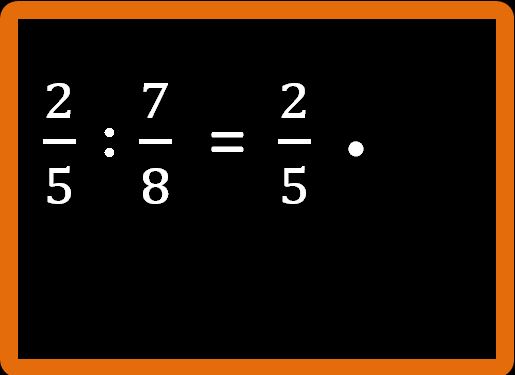
E adesso dobbiamo scrivere l’inverso della seconda frazione. Ti ricordo che la frazione inversa (come dice il nome stesso) si ottiene invertendo il numeratore con il denominatore. Quindi:
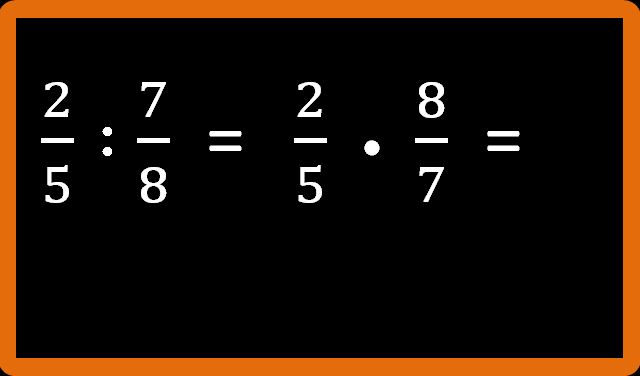
Ora abbiamo a che fare con una moltiplicazione tra frazioni che sappiamo manipolare. Se non ti ricordi come si esegue potresti dare un’occhiata al mio articolo cliccando qui.
In questo caso, dato che non possiamo semplificare in croce, è sufficiente moltiplicare il numeratore della prima per il numeratore della seconda, cioè 2 · 8 = 16
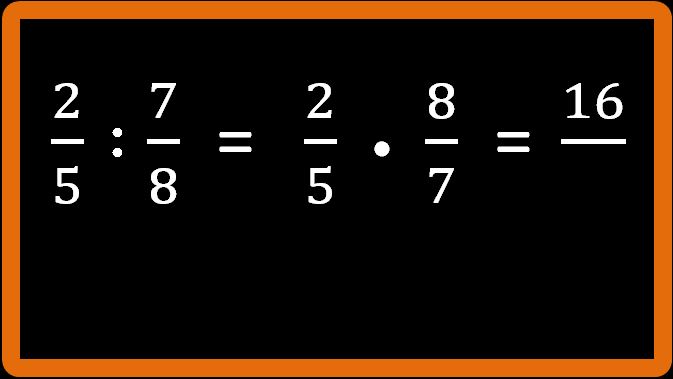
E ora moltiplichiamo il denominatore della prima per il denominatore della seconda, cioè 5 · 7 = 35.
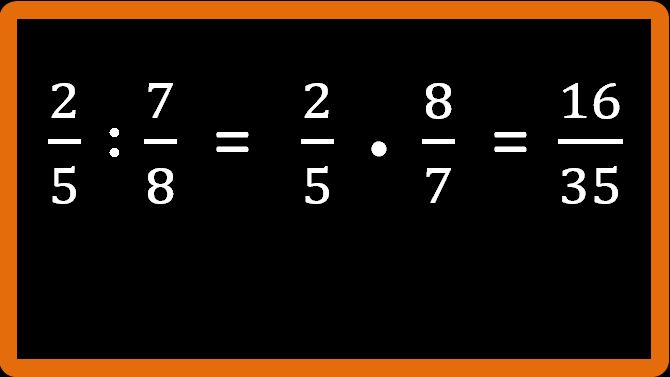
Abbiamo concluso. 16 fratto 35 è il risultato che stavamo cercando.
Iscriviti al mio canale youtube
Esempio 2
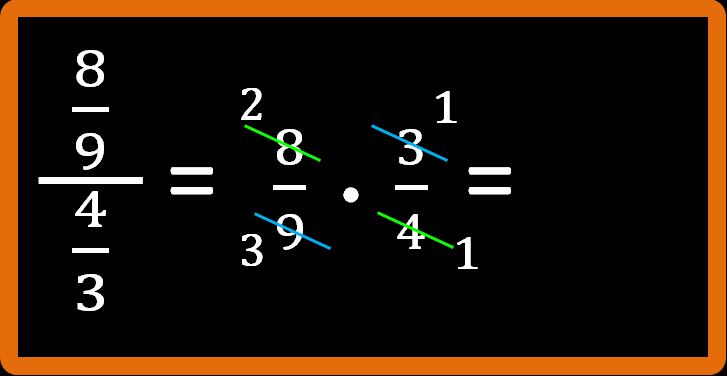
Facciamo un altro esempio di divisione tra frazioni. Cerchiamo di calcolare la seguente frazione tra frazioni. Ti suggerirei di provarci prima da solo. Nessuno ti rimprovererà se sbaglierai. Lavora nel modo più sereno possibile. Nei primi esercizi è normale sbagliare. Con la pratica riuscirai a sbagliare sempre meno.
Procediamo:
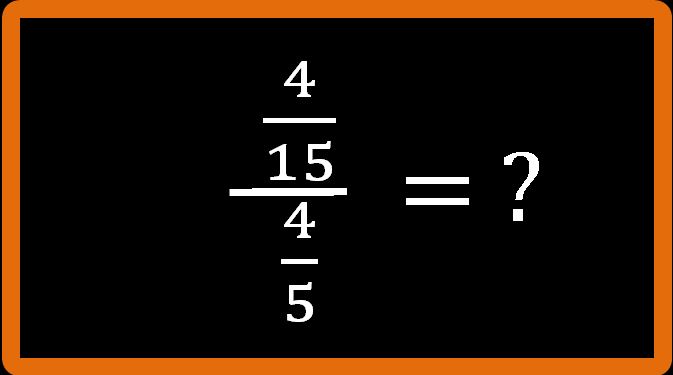
Per i primi esercizi facciamo tutti i passaggi, poi quando avremo un minimo di dimestichezza potremo saltarne qualcuno. Riscriviamo sotto forma di divisione:
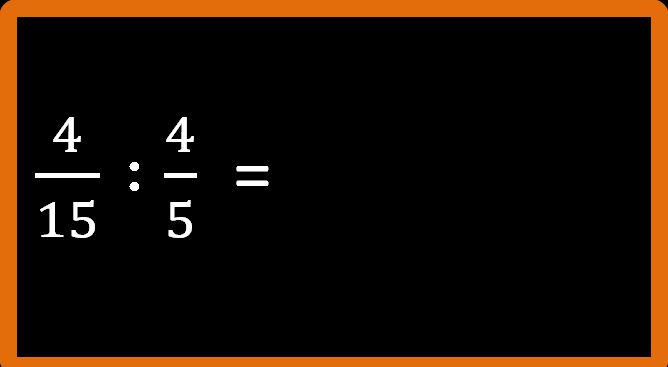
Ora riscriviamo la prima e mettiamo il segno della moltiplicazione al posto di quello della divisione:
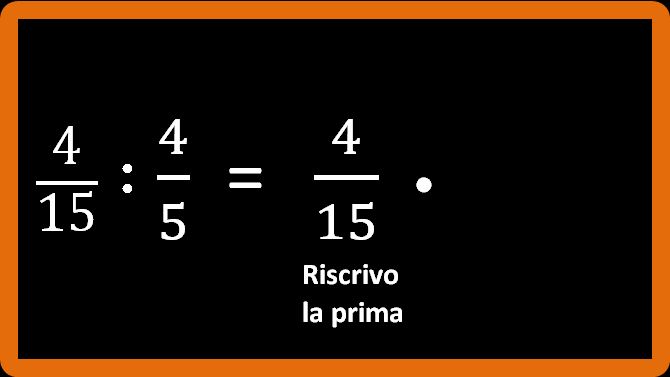
E ora scrivo l’inverso della seconda frazione:

Adesso semplifico in croce il 4 al numeratore della prima con il 4 al denominatore della seconda, dividendoli entrambi per 4 (se non ti ricordi come si semplifica in croce puoi leggere il mio articolo moltiplicazione tra frazioni e semplificazioni in croce):
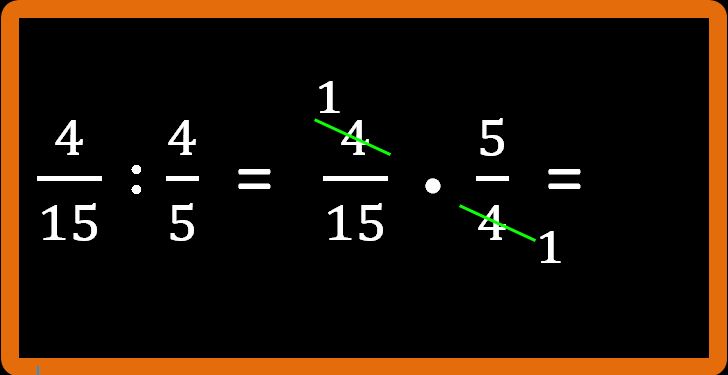
E semplifico in croce anche il 15 al denominatore della prima con il 5 al numeratore della seconda, dividendoli per 5:
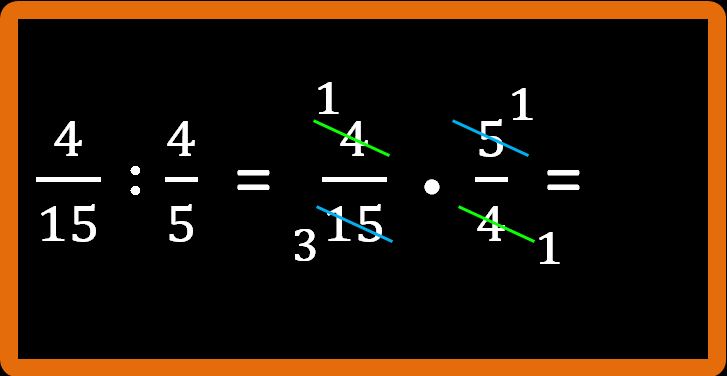
Non è più possibile semplificare. Quindi dobbiamo moltiplicare: numeratore per numeratore, cioè 1 · 1 = 1; e denominatore per denominatore, cioè 3 · 1 = 3.
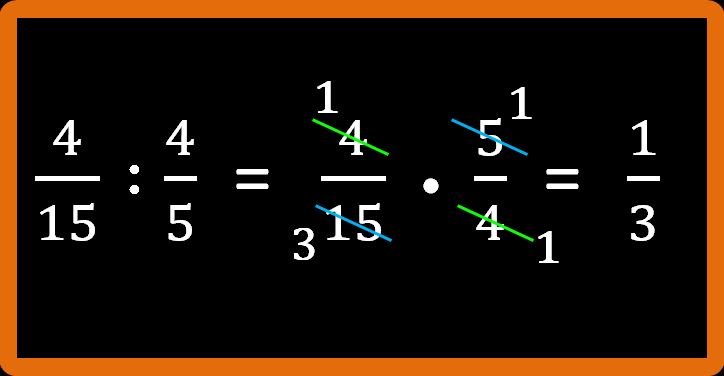
Il risultato che stavamo cercando è un terzo oppure 1 fratto 3. Tutto qui.
Esempio 3
Divisione tra frazioni: esempi ed esercizi. Ora prova a calcolare questa frazione da solo.
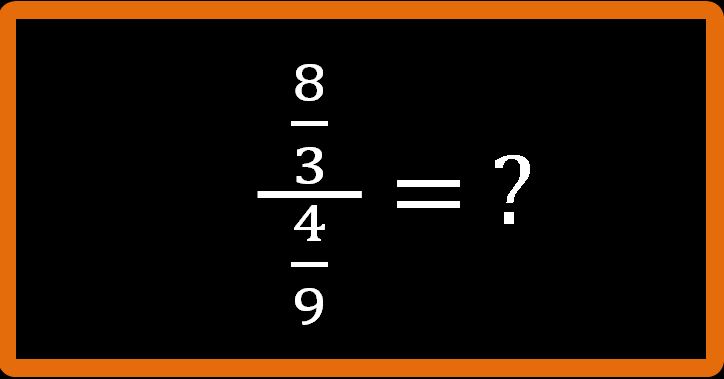
Otto terzi fratto quattro noni.
Ti dico qual è il risultato, ma prova ad arrivarci da solo. Non avere fretta. Rileggi quello che abbiamo fatto. Fai tutti i procedimenti necessari e se non ti riesce al primo tentativo non arrenderti. Cancella tutto e riprova.
Buon lavoro.
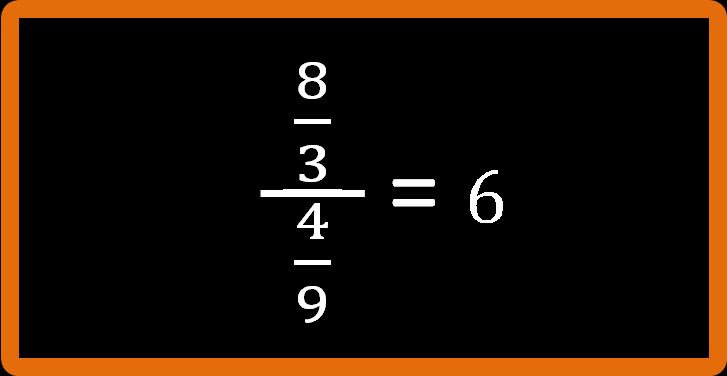
Il risultato che avresti dovuto ottenere è 6. Molto bene.
Se vuoi vedere altri esercizi svolti, puoi cliccare sul tasto che vedi subito sotto ‘Altri esercizi’.
Esercizi
Adesso prova da solo. Possiedi tutti gli strumenti necessari per eseguire qualsiasi divisione tra frazioni. Il primo esercizio è già svolto e serve per darti una guida. Non ti do i risultati, questo per abituarti ad avere fiducia in quello che scrivi. E poi, quando farai la verifica di matematica i risultati non li avrai, quindi meglio abituarsi.
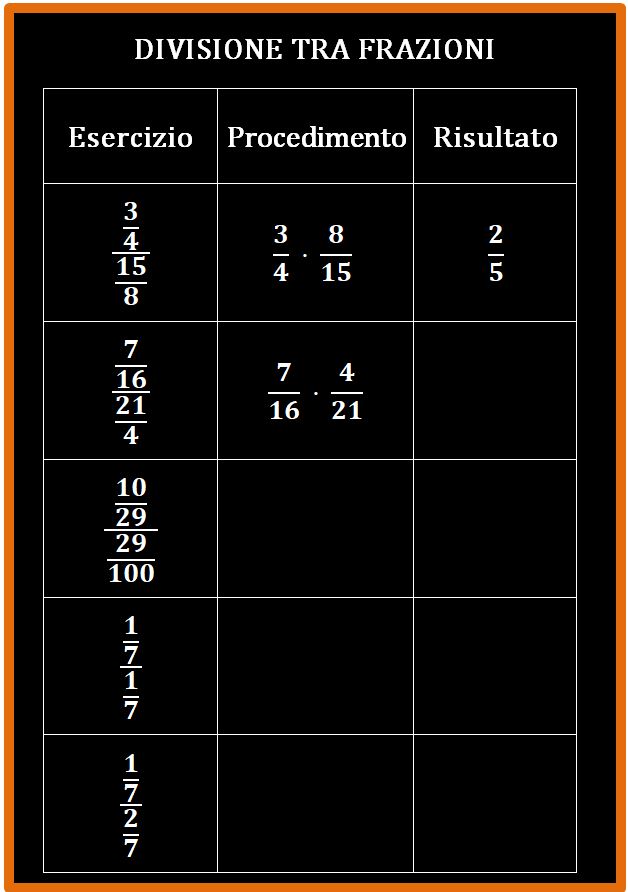
Buon lavoro.
ESERCIZI IN PDF
Se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto.
![]() Divisione tra frazioni – Esercizi.pdf
Divisione tra frazioni – Esercizi.pdf
Buon lavoro.
A questo link della Casa Editrice Zanichelli trovi le tavole numeriche. Puoi semplicemente consultarle oppure puoi scaricarle come file pdf seguendo le istruzioni che trovi alla fine di questo mio articolo.
Se hai dubbi o vuoi segnalare un errore puoi lasciare un commento o scrivere alla casella mail: matematica.facile@libero.it; sarò grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.