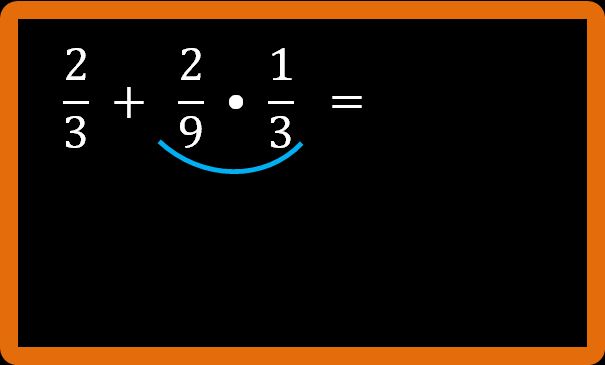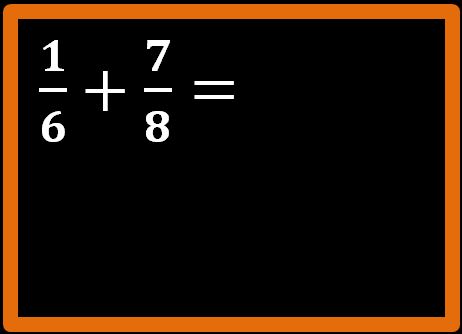Dopo avere imparato a eseguire la somma, la moltiplicazione, la divisione tra frazioni e avere anche imparato come si sviluppa la potenza di una frazione, è arrivato il momento di mettere tutto assieme. È arrivato il momento di una introduzione alle espressioni con le frazioni. Non ti preoccupare, con 5 minuti di impegno sarà tutto più chiaro.
Nell’eseguire un’espressione vanno rispettate alcune regole, alcune precedenze come quando sei in strada a piedi o in bicicletta. Infatti per strada quasi senza accorgertene rispetti alcune regole di precedenza. Per esempio se hai il semaforo rosso ti fermi per fare passare chi ha il semaforo verde. Allo stop ti fermi. Se un pedone sulle striscie deve attraversare la strada, ti fermi per farlo passare. Anche nelle espressioni ci sono alcune regole da seguire. Poche precedenze, ma che vanno rispettate.
Dopo questa breve introduzione alle espressioni e dopo avere letto come si eseguono le espressioni con le frazioni sarai in grado di risolvere un’ espressione del genere o anche più difficili:
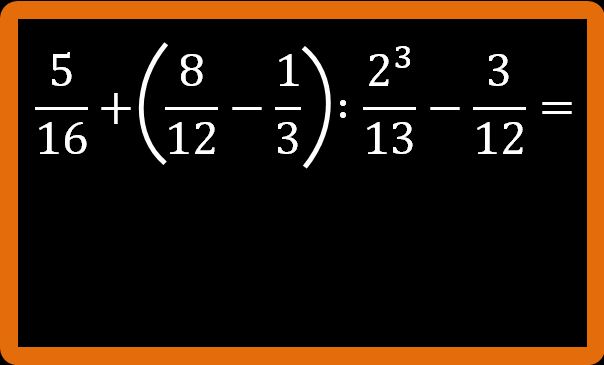
Ti anticipo subito che le precedenze che devi rispettare per risolvere le espressioni con le frazioni sono le stesse che hai imparato quando hai studiato le espressioni con i numeri naturali. Quindi alla fine niente di nuovo. Passiamo subito a eseguire qualche esercizio.
Esercizio svolto
Calcoliamo l’espressione scritta nella lavagna che vedi sotto:
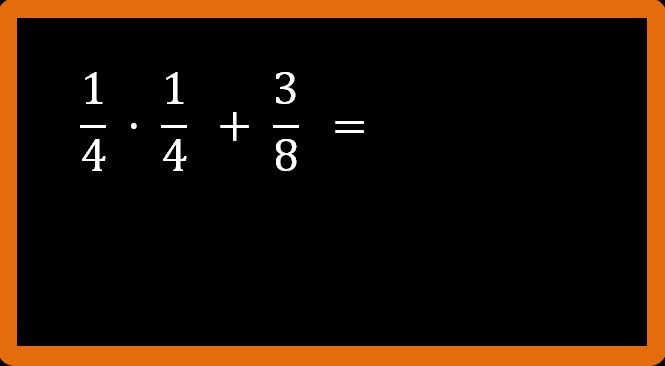
Precedenze da rispettare
Ecco quali sono le operazioni che hanno la precedenza quando si esegue una espressione con frazioni.
- Ridurre ai minimi termini (quando possibile). Se vuoi ripassare come si fa puoi leggere questo mio articolo ridurre una frazione ai minimi termini;
- Operazioni dentro le parentesi (tonde, quadre e graffe);
- Moltiplicazioni e divisioni. In questo articolo trovi come eseguire le moltiplicazioni tra frazioni. Invece cliccando qui si aprirà una nuova pagina nella quale potrai leggere come si esegue una divisione tra frazioni.
- Addizioni e sottrazioni procedendo da sinistra verso destra (la stessa direzione in cui stai leggendo in questo momento). Se non ti ricordi come si eseguono potresti dare un’occhiata a questo mio articolo addizione e sottrazione tra frazioni.
Torniamo alla nostra espressione. Tutte le frazioni sono già ai minimi termini e non ci sono parentesi, quindi eseguiamo prima la moltiplicazione. Io traccio un archetto sotto l’operazione che stiamo eseguendo, ma non è necessario. Serve solo per capire quello che stiamo facendo.
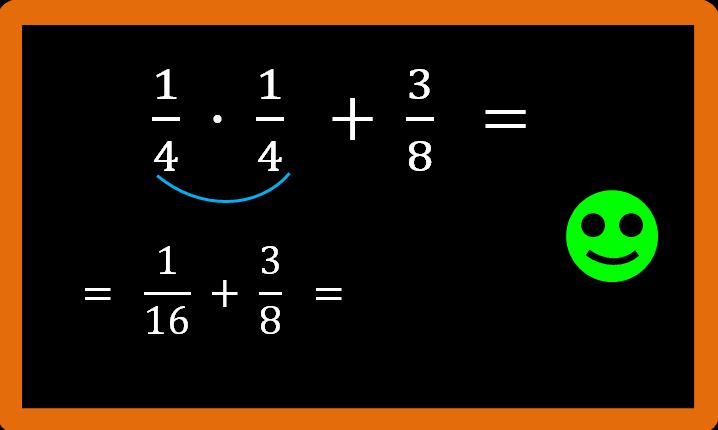
Adesso non ci resta che seguire l’addizione. Dovremmo calcolare il minimo comune multiplo tra i denominatori, ma osserviamo bene. Il primo denominatore è 16, invece il secondo denominatore è 8. Dato che 16 è un multiplo di 8 (infati 8 · 2 = 16) possiamo subito dire che 16 è il minimo comune multiplo. Questo è un caso particolare di m.c.m. Puoi ripassare i casi particolari di m.c.m. leggendo questo mio articolo. Determinato l’m.c.m. possiamo procedere con i calcoli:
Per la prima frazione otteniamo: 16 : 16 = 1; 1 · 1 = 1
Per la seconda frazione invece otteniamo: 16 : 8 = 2; 2 · 3 = 6
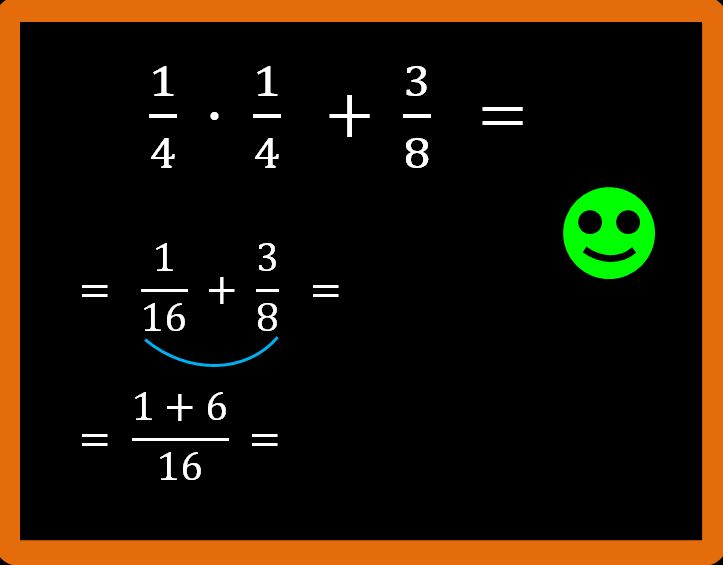
Adesso dobbiamo solo eseguire l’addizione al numeratore.

Sette sedicesimi è il risultato che stavamo cercando.
link utili
Le tavole numeriche sono uno strumento molto utile. Puoi usarle in classe e puoi anche usarle durante una verifica. Di solito si trovano all’interno del primo volume del libro di matematica, però può capitare di perderle (in realtà sono la prima cosa che gli studenti perdono). Se poi hai comprato il libro di seconda mano è quasi impossibile che tu le abbia trovate. Niente paura. Facendo click su questo link della Casa Editrice Zanichelli puoi consultare le tavole. Le puoi anche scaricare sul tuo pc come file pdf per poterle consultare off-line e averle sempre a disposizione. Se non ti ricordi come si scarica un file puoi seguire le istruzioni che trovi alla fine di questo mio articolo.
Se hai domande o vuoi segnalare un errore, puoi scrivere alla casella mail: matematica.facile@libero.it , saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.