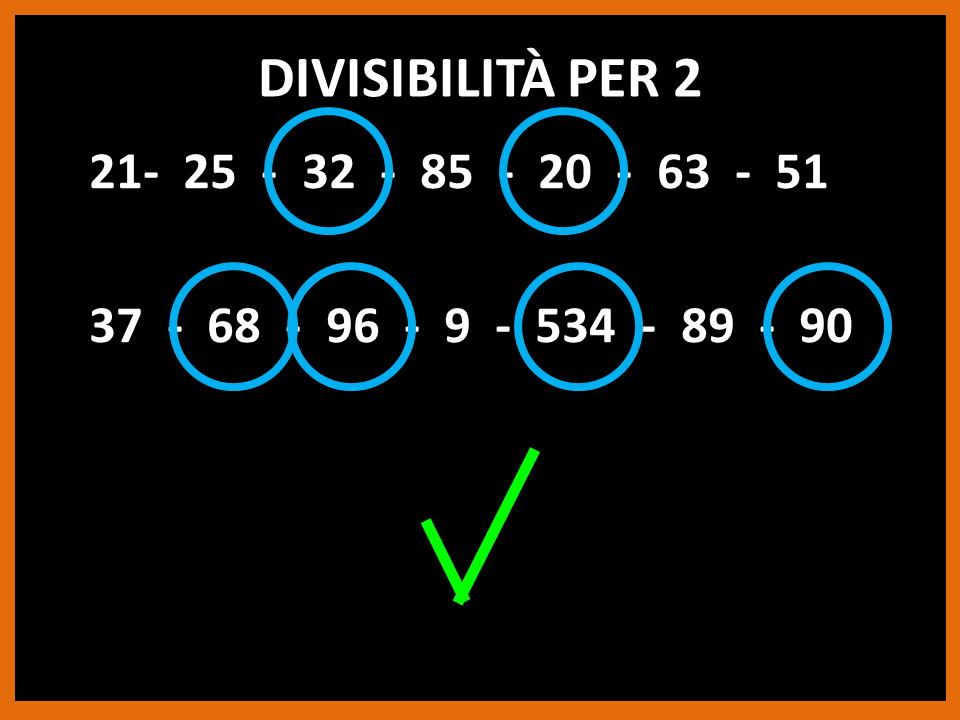
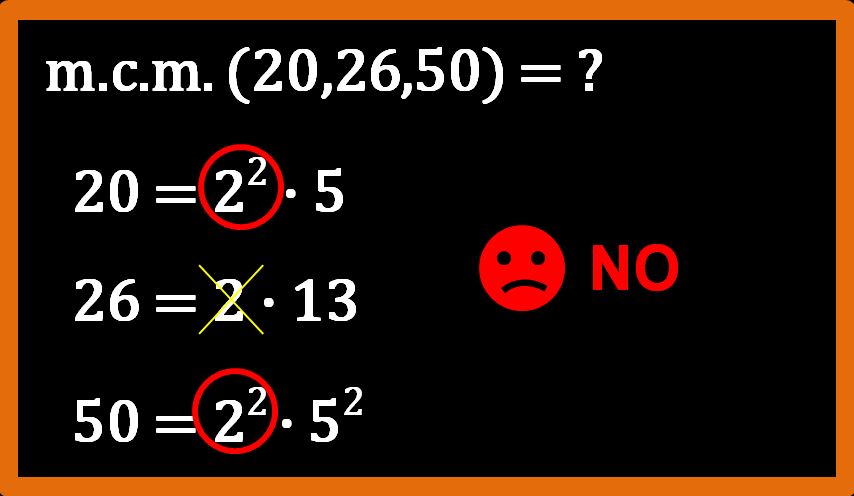In un articolo precedente abbiamo visto cos’è il minimo comune multiplo e come si calcola. In questo articolo vedremo alcuni casi particolari di minimo comune multiplo. Infatti a volte l’ m.c.m. può essere uguale a uno dei due numeri. Facciamo un esempio per capire meglio quanto detto.
Indice
Esempio 1
Proviamo a calcolare l’m.c.m. tra 15 e 45. Scomponiamo in fattori i due numeri, scriviamoli sotto forma di scrittura esponenziale.
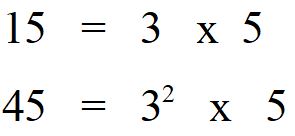
Fatto questo applichiamo la regola: “Per calcolare l’ m.c.m. bisogna moltiplicare i fattori comuni e non comuni presi una volta con il maggiore esponente” .
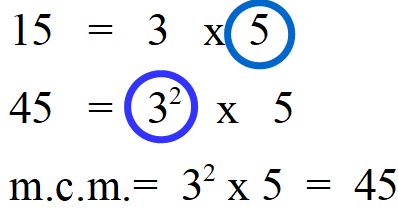
Come vedi l’m.c.m. in questo caso corrisponde a uno dei due numeri di partenza. Questo è un caso particolare e succede tutte le volte che uno dei due numeri è multiplo dell’altro. Nel nostro esempio infatti 45 è multiplo di 15, poichè 15 x 3 = 45.
Grazie a questa conoscenza a volte in alcuni esercizi puoi fare a meno di calcolare l’m.c.m.. Infatti se un numero è il multiplo dell’altro, allora l’ m.c.m. sarà proprio quel numero.
Esempio 2
Facciamo un paio di esempi con i numeri. Supponiamo di voler trovare l’m.c.m. tra 9 e 27.
m.c.m. (9,27) = ?
Se mi accorgo che 27 è multiplo di 9 (infatti 9 x 3 = 27) allora posso fare a meno dei calcoli e dire subito che l’m.c.m. è 27. Se non ti fidi, puoi provare a scomporre in fattori primi sia il 9 che il 27, applicare la regola e vedrai che otterrai come m.c.m. il numero 27.
m.c.m. (9,27) = 27
Esempio 3
Ancora un altro esempio che riguarda questo caso particolare. Troviamo l’m.c.m tra 6 e 42.
m.c.m. (6, 42) = ?
Anche in questo caso, posso evitare di fare calcoli perchè 42 è multiplo di 6 ( 6 x 7 = 42). Allora l’m.c.m sarà 42.
m.c.m. (6, 42) = 42
Esempio 4
Ora che sappiamo cos’è l’m.c.m. e conosciamo la regola per calcolarlo facciamo qualche esempio con i numeri. Non ti preoccupare se nei primi esercizi commetterai qualche errore, è normale. Esercitarsi serve proprio a questo. Cominciamo, carta e penna alla mano.
Calcoliamo l’m.c.m. tra 21 e 54.
Si comincia scomponendo in fattori primi i due numeri
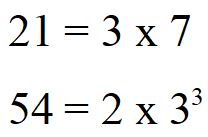
Scegliamo ora i fattori che ci serviranno per calcolare l’m.c.m..
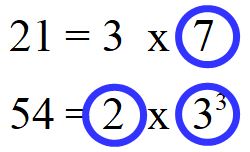
Tra il 3 presente nella scoposizione del 21 e il 33 presente nella scomposizione del 54, dobbiamo scegliere il 33 poichè ha l’esponente maggiore.
Poi dobbiamo scegliere il 7 che compare nella scomposizione del 21.
E per ultimo dobbiamo considerare anche il due che compare nella scomposizione del 54.
Passiamo ora al calcolo, cioè moltiplichamo tra loro i fattori che abbiamo scelto.
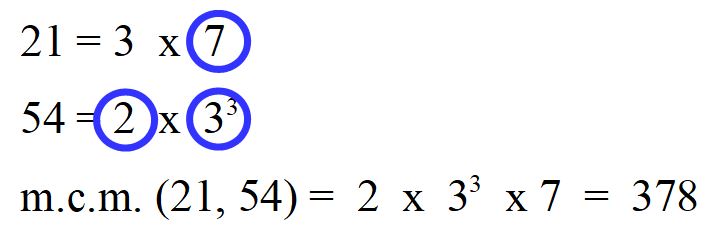
Abbiamo trovato che l’m.c.m. tra 21 e 54 è 378
Come dici? 378 ti sembra un numero grande. Non preoccuparti. Quando calcoli l’m.c.m. otterrai spesso numeri grandi, a volte anche partendo da numeri piccoli, come vedremo nel prossimo esempio.
Esempio 5
Vediamo adesso un altro esempio di casi particolari di minimo comune multiplo. Calcoliamo l’ m.c.m. tra 15 e 14.
Si comincia come sempre scomponendo in fattori primi i due numeri.
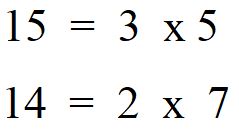
Scegliamo i fattori che ci serviranno per calcolare l’m.c.m..
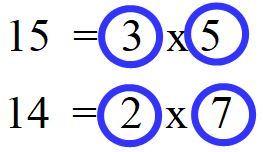
Anche se può sembrarti strano, in questo caso dobbiamo scegliere tutti i fattori presenti nelle scomposizioni.
Moltiplichiamoli tra loro e troviamo l’m.c.m..
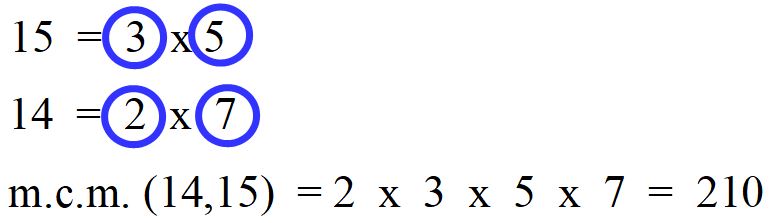
Il risultato è 210
Può sembrarti di avere ottenuto un numero grande, ma è il risultato corretto. Esercizio concluso.
Esercizi in pdf
Adesso possiedi tutti gli strumenti per calcolare il minimo comune multiplo anche nei casi particolari. Puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Lavora con calma e senza fretta. Buon lavoro
![]() Casi particolari di minimo comune multiplo – ESERCIZI.pdf
Casi particolari di minimo comune multiplo – ESERCIZI.pdf
Se hai perso le tavole numeriche, puoi consultarle a questo link della Casa Editrice Zanichelli, puoi anche scaricarle come file pdf per poterle avere sempre sul pc anche off-line.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it; saremo grati a tutti quei lettori che ci segnaleranno eventuali errori presenti nell’articolo.