Bene, sai già calcolare il minimo comune multiplo tra 2 numeri. E abbiamo anche visto alcuni casi particolari di m.c.m.. Se hai ancora qualche difficoltà ti consiglio di leggere il mio articolo sul calcolo del m.c.m.. Ma in alcuni esercizi ti verrà chiesto di calcolare il minimo comune multiplo tra 3 numeri. Niente paura, il procedimento è lo stesso, solo un po’ più lungo di quello del calcolo dell’ m.c.m. tra 2 numeri.
Cominciamo subito con qualche esempio numerico, così ti renderai conto che poi non è affatto difficile calcolare il minimo comune multiplo tra 3 numeri.
Indice
Esempio 1
Supponiamo di voler calcolare l’ m.c.m. tra 18, 20 e 21.
La prima cosa da fare è scomporre in fattori primi i 3 numeri. Se non ti ricordi come si fa a scomporre un numero in fattori primi, puoi dare un’occhiata al mio articolo: la scomposizione in fattori primi.
Scomposizione in fattori primi
18 = 2 · 32
20 = 22 · 5
21 = 3 · 7
Scelta dei fattori
Adesso dobbiamo scegliere i fattori che ci permetteranno di calcolare l’ m.c.m..
18 = 2 · 32
20 = 22 · 5
21 = 3 · 7
Cerchiamo di capire perchè abbiamo scelto proprio quei fattori. Ragioniamo assieme ricordando cosa dice la regola: “Per calcolare l’ m.c.m. si devono scegliere i fattori comuni e non comuni presi una sola volta con l’esponente maggiore“.
Partiamo dal fattore 2. Il numero 2 compare nella scoposizione del 18 con esponente 1 (ricorda che 2 = 21) e nella scomposizione del 20 con esponente 2. Seguendo quello che dice la regola, dobbiamo scegliere solo quello con l’esponente maggiore.
Discorso simile si può fare per il 3. Infatti il numero 3 compare con esponente 2 nella scomposizione del 18 e con esponente 1 nella scomposizione del 21. Siccome dobbiamo scegliere quello con esponente maggiore, scegliamo il 32.
Siccome dobbiamo scegliere anche i fattori non comuni, dobbiamo considerare anche il 5 che compare nella scomposizione del 20.
E per lo stesso motivo scegliamo anche il 7 che compare nella scomposizione del 21.
Calcolo dell’ m.c.m.
Dobbiamo adesso calcolare l’m.c.m. semplicemente moltiplicando tra loro i fattori che abbiamo scelto.
m.c.m.(18, 20, 21) = 22 · 32 · 5 · 7 = 1260
Come ti ho già detto in un articolo precedente, non preoccuparti se ottieni numeri grandi. Quando si calcola l’ m.c.m. capita spesso.
Esempio 2
Calcoliamo l’ m.c.m. tra 10, 11 e 12. Come sempre dobbiamo partire dalla scomposizione in fattori primi dei numeri considerati. Ti consiglio di prendere carta e penna e provare a fare l’esercizio assieme.
Scomposizione in fattori primi
10 = 2 · 5
11 = 11
12 = 22 · 3
Come vedi non è possibile scomporre il numero 11 in fattori primi perchè il numero 11 è un numero primo. Quindi qualsiasi numero primo non può essere scomposto.
Scelta dei fattori
Come sempre, il passo successivo dopo avere scomposto in fattori primi è scegliere quali fattori considerare per calcolare l’ m.c.m..
10 = 2 · 5
11 = 11
12 = 22 · 3
Non scegliamo il 2, ma scegliamo il 22, perchè ti ricordo che va scelto il numero con l’esponente maggiore.
Calcolo dell’m.c.m.
Per calcolare l’m.c.m. dobbiamo moltiplicare tra loro i fattori che abbiamo scelto.
m.c.m = 5 · 11 · 22 = 660
Il risultato che stavamo cercando è 660. Non preoccupiamoci se otteniamo un numero grande, è possibile.
Esempio 3
Calcoliamo l’m.c.m. tra 20, 26 e 50.

Scomposizione in fattori primi
Il primo passaggio da eseguire è la scomposizione in fattori primi dei tre numeri che abbiamo considerato.
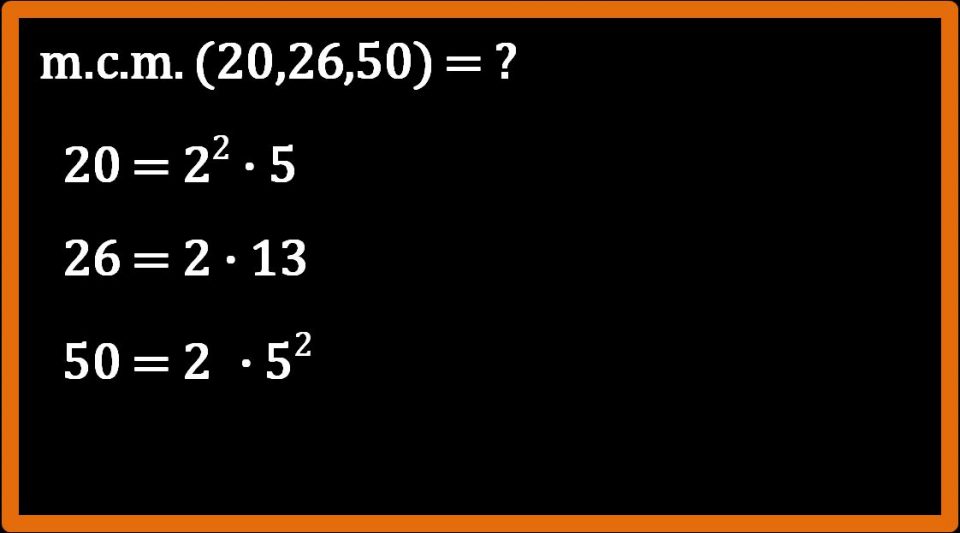
Scelta dei fattori
Ora, ricordando quello che dice la regola, dobbiamo scegliere i fattori che ci permetteranno di calcolare l’m.c.m. in modo corretto.
Il fattore 2 compare in tutte le scomposizioni:
- in quella del 20 con esponente 2;
- in quella del 26 con esponente 1 (ricordati che 2 = 21);
- in quella del 50 con esponente 1 (come in quella del 26).
Noi dobbiamo scartare il 2 con esponente 1 (perchè dobbiamo scegliere il fattore con esponente più grande). Rimane solo quello con esponente 2 presente nella scomposizione del 20.
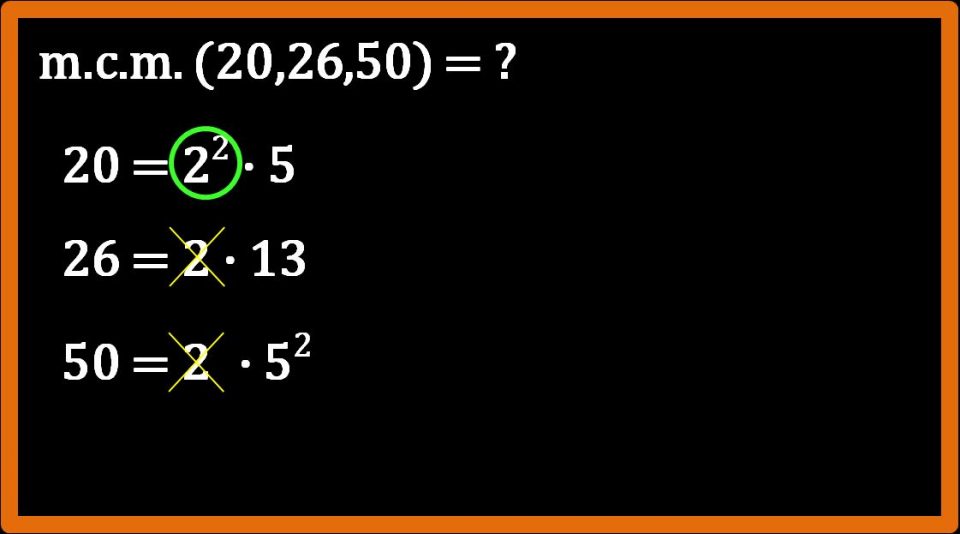
Passiamo ora al fattore 5.
Il fattore 5 compare nella scomposizione:
- del 20 con esponente 1;
- del 50 con esponente 2.
Noi dobbiamo scegliere quello con esponente maggiore. Quindi quello con esponente 2.
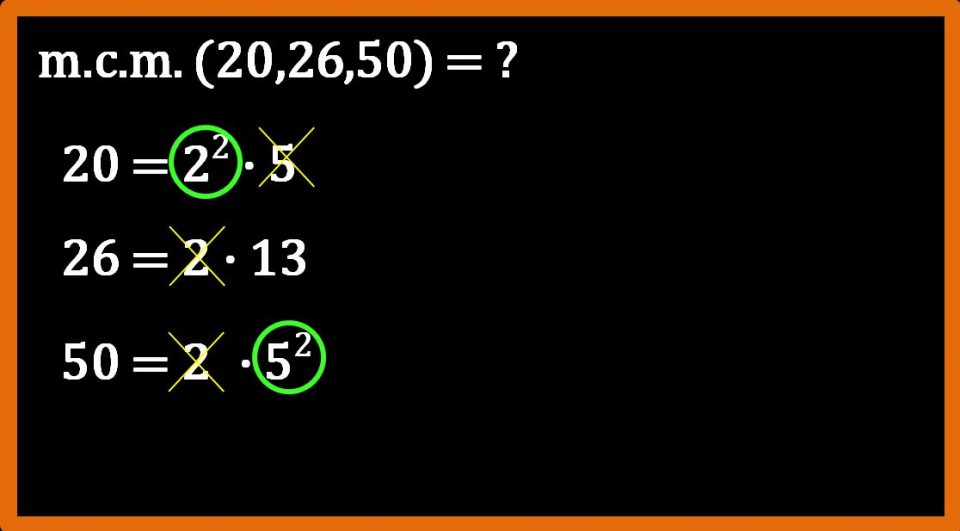
L’ultimo fattore da prendere in considerazione è il 13, che compare solo nella scomposizione del 26, ma la regola dice: “fattori comuni e non comuni”, per cui anche il 13 va scelto.

Calcolo dell’m.c.m.
Non ci rimane che moltiplicare tra loro i fattori che abbiamo scelto:
22 • 52 • 13 = 1300

Esercizio concluso. Il risultato che stavamo cercando è 1300. Non preoccuparti se ottieni numeri grandi, con il minimo comune multiplo capita.
Esercizi in pdf
Adesso se vuoi puoi metterti alla prova con gli esercizi che trovi nei file pdf sotto. Lavora con calma, non stai facendo una gara di velocità. Non avere fretta e non ti preoccupare se sbagli. Sbagliando si impara.
![]() Minimo comune multiplo tra 3 numeri – Esercizi.pdf
Minimo comune multiplo tra 3 numeri – Esercizi.pdf
![]() Minimo comune multiplo tra 3 numeri – Esercizi 2.pdf
Minimo comune multiplo tra 3 numeri – Esercizi 2.pdf
Buon lavoro.
Se vuoi puoi esercitarti con gli esercizi che trovi sotto. Cliccandoci su si aprirà una nuova pagina che ti permetterà di consultare gli esercizi, ma se vuoi puoi anche scaricarli e stamparli. Buon lavoro.
Link utili
Se hai domande o vuoi segnalare un errore puoi lasciare un commento o scrivere alla nostra casella mail: matematica.facile@libero.it; saremo grati ai lettori che segnaleranno eventuali errori.