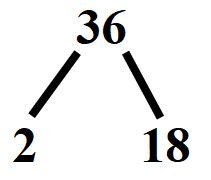
Oggi pomeriggio hai provato a svolgere gli esercizi che aveva assegnato la prof, ma hai avuto qualche difficoltà? Niente paura, con un po’ di impegno imparerai come si esegue la scomposizione in fattori primi di qualsiasi numero.
Però prima di cominciare è necessario avere presente che differenza c’è tra numeri primi e numeri composti. Se in questo momento la differenza non ti è tanto chiara, potresti leggere il mio articolo: i numeri primi e i numeri composti.
Se invece hai già capito la scomposizione e vuoi dare un’occhiata ad alcuni esercizi svolti puoi leggere il mio articolo: esercizi svolti di scomposizione in fattori primi.
Riassumendo, possiamo dire che tutti i numeri possono essere raggruppati all’interno di due grandi recinti: quello dei numeri primi e quello dei numeri composti.
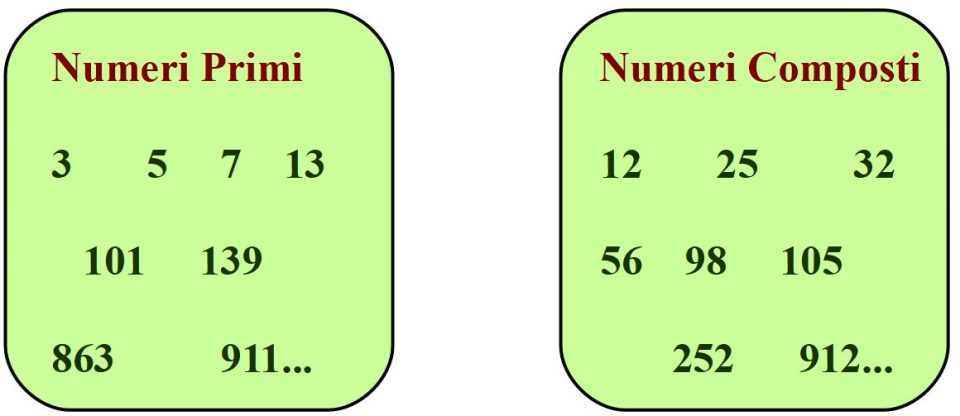
Questi recinti in matematica si chiamano insiemi. Nella figura non sono scritti tutti i numeri primi, ma solo alcuni. Lo stesso vale per i numeri composti.
Indice
- Cosa vuol dire: “Scomposizione in fattori primi”
- Primo esempio
- Secondo esempio
- Terzo esempio
- Altri esempi di scomposizione in fattori primi
- Esempio svolto su Youtube
- Esercizi in pdf
Esercizio veloce su Google Moduli
Se vuoi un esercizio su Google Moduli è sufficiente cliccare qui è si aprirà una nuova pagina con un Modulo Google di 10 domande.
Buon lavoro.
Cosa vuol dire scomposizione in fattori primi
Cominciamo a fare sul serio e cerchiamo di capire cosa vuol dire ‘scomposizione in fattori primi‘. Esaminiamo le parole:
- Scomposizione : scomporre vuol dire dividere qualcosa negli elementi che la costituiscono. Facciamo un esempio. Supponiamo di voler scomporre un piatto di spaghetti al pomodoro nei suoi ingredienti. Otterremo la pasta da una parte e i pomodori dall’altra parte. Facciamo un altro esempio, osserviamo la figura sotto.

Scomponiamola negli elementi che la compongono. Otterremo i singoli rettangoli, come puoi vedere sotto.
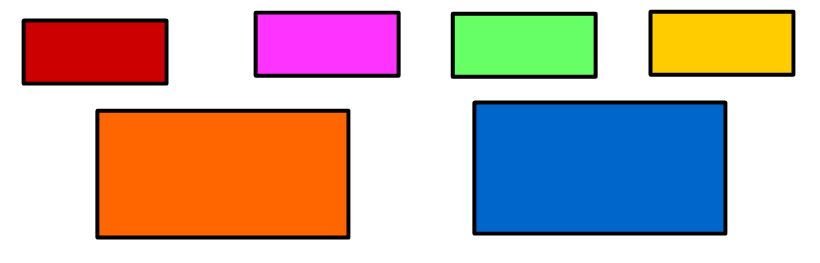
- Fattori : i fattori in matematica sono gli elementi della moltiplicazione. Per esempio nella moltiplicazione
2 · 5 = 10
i numeri 2 e 5 sono i fattori e 10 è chiamato prodotto.
Oppure ancora, nella motiplicazione
3 · 7 = 21
i fattori sono il numero 3 e il numero 7. Invece il numero 21 è chiamato prodotto della moltiplicazione o semplicemente prodotto.
- Primi : in questo caso primi vuol dire che i fattori di cui parlavamo sopra devono essere numeri primi.
Se vuoi ripassare il concetto di numeri primi puoi leggere il mio articolo i numeri primi e i numeri composti.
Procedimento per eseguire la scomposizione in fattori primi
Per eseguire la scomposizione in fattori primi di un numero si può procedere in diversi modi. Di seguito ti mostrerò i due modi che vengono usati più spesso:
- la scomposizione in colonna e
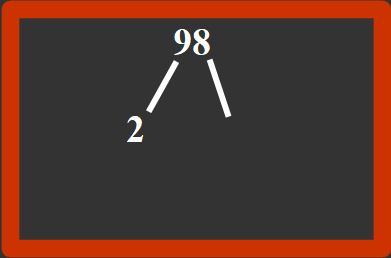
- la scomposizione ad albero.
Vedrai che i due metodi sono uguali nel procedimento, ma diversi nella rappresentazione. Cominciamo con il fare degli esempi e capirai subito le differenze.
Esempio 1: scomposizione in fattori primi del numero 6
Scomponiamo in fattori primi il numero 6 usando entrambi i metodi, prima quello in colonna e poi quello ad albero.
Scomposizione del numero 6 in colonna
Vediamo come si procede. È più difficile spiegarlo a parole che farlo nella pratica.
Si inizia scrivendo il numero 6 e tracciando una riga verticale accanto al numero.

Ora dobbiamo cominciare a scomporre il 6. Per fare ciò lo dobbiamo dividere. Ma per quale numero? Dobbiamo scegliere un numero primo, ma quale? Non c’è una regola fissa. Se il numero da scomporre è pari, io preferisco partire sempre dividendo per 2 (che è il primo tra i numeri primi).
Dall’ altra parte della riga, quindi, scriveremo 2.

Il numero 2 nel nostro esempio è il primo fattore di scomposizione.
Ora bisogna fare la divisione :
6 : 2
e scrivere il risultato della divisione sotto il 6. Naturalmente il risultato è 3.
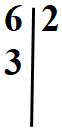
Dobbiamo procedere con le divisioni fino a quando il risultato che otterremo non sarà 1. Nel nostro esempio dobbiamo dividere il numero 3. Non possiamo dividerlo per 2.
L’unico numero primo per cui possiamo dividere il 3, è se stesso (poiché 3 è un numero primo). Quindi scriveremo così:
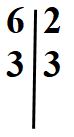
Eseguiamo la divisione
3 : 3
che ci dà come risultato 1. Andremo a scrivere 1 nella stessa colonna del 6 e del 3. Abbiamo finito.
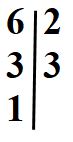
I fattori primi in cui viene scomposto il 6 sono 2 e 3 (li trovi nella colonna di destra). Oppure, detta in un altro modo: i fattori primi che compongono il 6 sono: il 2 e il 3 che abbiamo scritto nella colonna di destra.
6 = 2 · 3 che è il risultato che stavamo cercando.
Chiaro? Meglio fare un altro esempio con altri numeri.
Esempio 2: scomposizione in fattori primi del numero 36 in colonna
Cominciamo come sempre scrivendo il 36 e tracciamo una riga alla destra del numero.
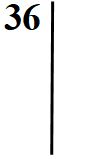
36 è un numero pari, quindi si può dividere per 2. Scriveremo il 2 a destra della riga.
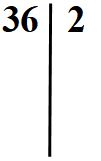
Ora dobbiamo eseguire la divisione 36 : 2 e scrivere il risultato ottenuto sotto il 36. Non abbiate fretta nel fare i calcoli. È naturale nei primi esercizi essere un po’ lenti e insicuri. Abbiamo cominciato tutti così. Esercitarsi serve proprio a questo. La pratica ti porterà a essere più veloce e a sbagliare sempre meno.

Ora dobbiamo dividere il 18. Dato che è un numero pari, possiamo dividerlo per 2. Scriveremo un altro 2 a fianco del 18.
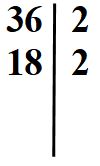
Eseguiamo la divisione 18 : 2 e scriviamo il risultato sotto il 18. Come vedi il procedimento è ripetitivo. Capito il meccanismo, poi diventa più agevole.
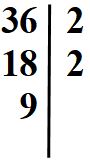
Si continua sempre nello stesso modo, cioè dobbiamo dividere il 9 per un numero primo. L’unico numero primo per cui possiamo dividerlo è il 3. Scriveremo allora 3 nella colonna di destra, sotto il 2.
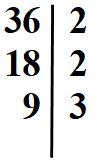
Eseguiamo la divisione 9 : 3 e scriviamo il risultato sotto il 9.
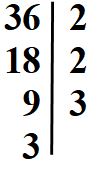
Dobbiamo ora dividere il 3. L’unico numero primo per cui lo possiamo dividere è se stesso, cioè dobbiamo fare la divisione 3 : 3. Poi scriviamo il risultato nella colonna di sinistra.
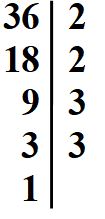
Allunghiamo la riga se necessario. Abbiamo ottenuto come risultato 1, questo vuol dire che abbiamo finito con le divisioni.
Nella colonna di destra possiamo leggere i fattori di scomposizione del numero 36. Devono essere tutti numeri primi. Se così non fosse vuol dire che abbiamo sbagliato da qualche parte.
I fattori primi
Stiamo arrivando alla conclusione dell’esercizio. Scriviamo il numero 36 come prodotto dei suoi fattori di scomposizione.
36 = 2 · 2 · 3 · 3
Ma avrai studiato sicuramente le potenze. La potenza ci permette di scrivere una moltiplicazione come quella di sopra in modo più sintetico, più breve.
36 = 22 · 32
Questo è il risultato che stavamo cercando.
Quella che hai appena letto si chiama scrittura esponenziale ed è il modo corretto di scrivere una scomposizione.
Non ti preoccupare se per i primi esercizi ti sembra di impiegare troppo tempo. Abbiamo cominciato tutti così. Poi con l’allenamento ed esercitandoti tutto diventerà più semplice, ma solo dopo un buon numero di esercizi. Cosa credi che Cristiano Ronaldo non si alleni? Ti sbagli, anzi è il primo ad arrivare e l’ultimo ad andarsene e questo vale per tutti i veri professionisti in qualsiasi ambito.
Procedimento scorretto⚠️
Vediamo ora un errore abbastanza comune che si può commettere quando si scompone in fattori primi.
Scomponiamo sempre il numero 36.
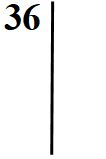
Iniziamo con le divisioni. Ricordandomi della tabellina del 6, decido di dividere il 36 per 6.
Infatti 6 · 6 = 36.
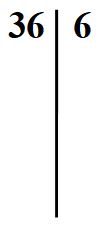
Anche se matematicamente è corretto dire che il 36 è divisibile per 6, nella scomposizione in fattori primi questo modo di procedere è sbagliato ⚠️⚠️⚠️.

Infatti nella colonna di destra possiamo scrivere solo numeri primi. E il 6 non è un numero primo. Per questo motivo il procedimento che abbiamo seguito in questo esempio è errato.
Procedimento corretto alternativo
Come ti ho già detto non esiste una regola fissa nello scegliere il numero per cui dividere. Quando abbiamo scomposto il 36 abbiamo iniziato dividendo per 2. Ma nessuno mi vieta di dividere per 3. Vediamo cosa succede.
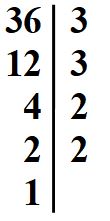
Dividendo per 3 otteniamo questo risultato. Scriviamo in modo esponenziale i fattori di scomposizione eseguendo tutti i passaggi.
I fattori primi
36 = 3 · 3 · 2 · 2 che diventa → 36 = 32 · 22
È lo stesso risultato a cui siamo arrivati con il primo procedimento. Infatti ti ricordo che la moltiplicazione gode della proprietà commutativa, cioè cambiando l’ordine dei fattori il risultato non cambia. Possiamo quindi scrivere
36 = 22 · 32
Questo è il modo che preferisco, cioè scrivere i fattori iniziando da quello con la base più piccola (nel nostro esempio il 2).
Esempio 3: scomposizione in fattori primi del 60
Procediamo con qualche altro esempio numerico.
Scomponiamo il numero 60. È un numero pari, quindi possiamo dividerlo per 2.
Scriviamo il 2 nella colonna di destra.
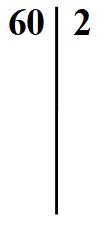
E il risultato della divisione nella colonna di sinistra sotto il 60.
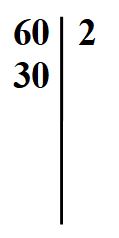
Procediamo con le divisioni. Ti ricordo: possiamo dividere solo usando numeri primi.
Anche 30 è un numero pari e quindi divisibile per 2.
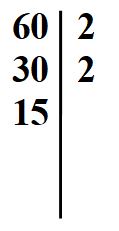
Otteniamo come risultato 15, che non è pari. Quindi dovremo cercare un altro divisore.
15 è divisibile per 3.
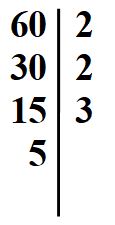
Il passaggio successivo è questo.
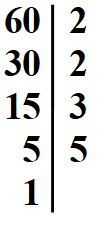
Abbiamo finito di scomporre. Ora scriviamo il 60 come prodotto di fattori primi, usando la scrittura esponenziale.
Forma esponenziale
60 = 22 · 3 · 5
Questo è il risultato che stavamo cercando.
Esempio 3. Procedimento alternativo
Naturalmente quello che abbiamo visto non è l’unico procedimento possibile. Di seguito vedi illustrato un altra strada possibile che è comunque giusta.
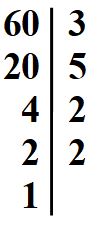
Nella colonna di destra sono presenti solo numeri primi ed è quello che vogliamo.
Il risultato della scomposizione è lo stesso.
60 = 3 · 5 · 22
Usando la proprietà commutativa della moltiplicazione possiamo scrivere in questo modo.
60 = 22 · 3 · 5
Lo stesso risultato trovato usando il primo procedimento.
Sono due strade diverse, ma entrambe giuste che portano allo stesso risultato corretto.
Adesso possiedi tutti gli strumenti per potere scomporre in fattori primi qualsiasi numero. Buon lavoro. E ricordati, non ti preoccupare se sbagli. Capita a tutti, l’importante è non arrendersi e riprovare.
Iscriviti al mio canale Youtube→matematicafacile
Esercizi in pdf
Adesso puoi provare da solo, hai gli strumenti necessari per eseguire gli esercizi. Non avere fretta di finire, non è una gara di velocità. E non ti preoccupare se sbagli. Sbagliare è normale. Buon lavoro.
Link utili
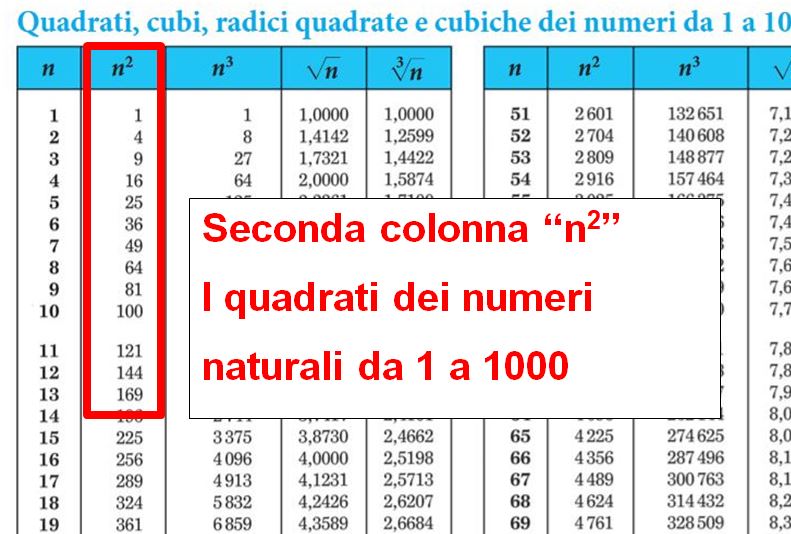
A questo link della Casa Editrice Zanichelli trovi le Tavole Numeriche. Puoi semplicemente visualizzarle oppure anche scaricarle sotto forma di file pdf facendo click sull’icona che trovi in alto a destra del documento.
Se hai dei dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it oppure contattarmi sulle mie pagine social di IG, FB o TT.
Nella pagina sono presenti link di affiliazione su cui si ottiene una piccola quota dei ricavi, senza variazioni dei prezzi.