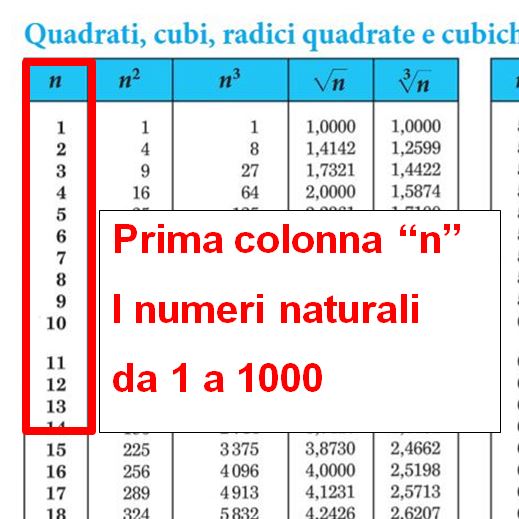
In questo articolo vedremo a cosa servono la terza, la quarta e la quinta colonna delle tavole numeriche. Vedremo anche come è possibile ricavare la radice quadrata di numeri maggiori di 1000. Inoltre a pagina 13 e 14 delle tavole vedremo i numeri primi dall’ 1 al 10000. Questi ti serviranno per esempio nella scomposizione in fattori primi.
Se hai perso le tavole numeriche non ti preoccupare, le puoi consultare e anche scaricare cliccando qui. Si aprirà una nuova pagina della Casa Editrice Zanichelli che offre appunto le tavole numeriche in formato pdf. Se invece vuoi ripassare cosa si trova nelle prime due colonne, potresti leggere il mio articolo come si usano le tavole numeriche.
iscriviti al nostro canale yotube
indice
- Terza colonna
- Quarta colonna
- Quinta colonna
- Radice quadrata di numeri maggiori di 1000
- Numeri primi da 1 a 10000
terza colonna
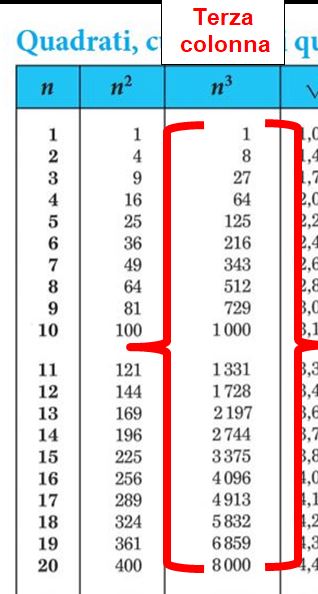
La terza colonna si chiama”n3 ” ( n sta per numero, in altre parole, la lettera n indica un numero qualsiasi). In questa colonna si trovano i cubi dei numeri naturali. Mi spiego meglio. Troviamo i numeri naturali elevati alla terza (si può anche dire elevati al cubo). Per esempio, se ci serve sapere quanto fa 4 elevato alla terza e non possiamo usare la calcolatrice e non ci va di fare i calcoli, possiamo usare le tavole.
43 = 4 · 4 · 4 = ?
Vediamo come si procede:
- Il primo passaggio da fare è andare a cercare il numero 4 nella prima colonna;
- troveremo il risultato nella terza colonna, cioè 43 = 64.
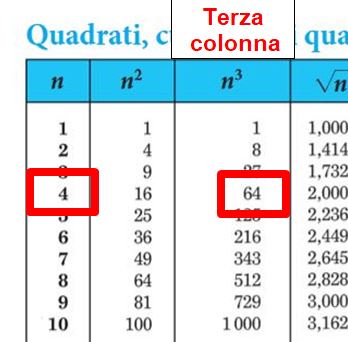
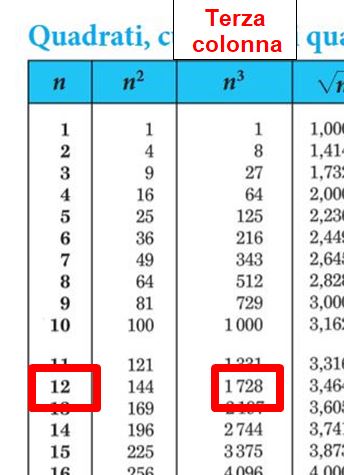
Facciamo un altro esempio: ci serve sapere quanto fa 123 ? Cerchiamo il 12 nella prima colonna, troveremo il risultato nella terza colonna. (Ricorda, le tavole possono essere utilizzate anche in classe anche durante le verifiche, per cui è molto importante saperle usare).
quarta colonna
Continuiamo a vedere come si usano la terza, la quarta e la quinta colonna delle tavole numeriche. Nella quarta colonna troviamo le radici quadrate. Questa colonna è particolarmente utile quando studierai il teorema di Pitagora. Facciamo un esempio. Vogliamo sapere la radice quadrata di 25.
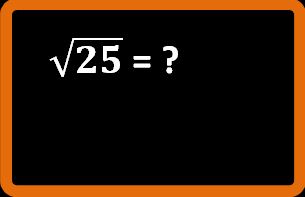
Cerchiamo il 25 nella prima colonna, troveremo il risultato nella quarta colonna.
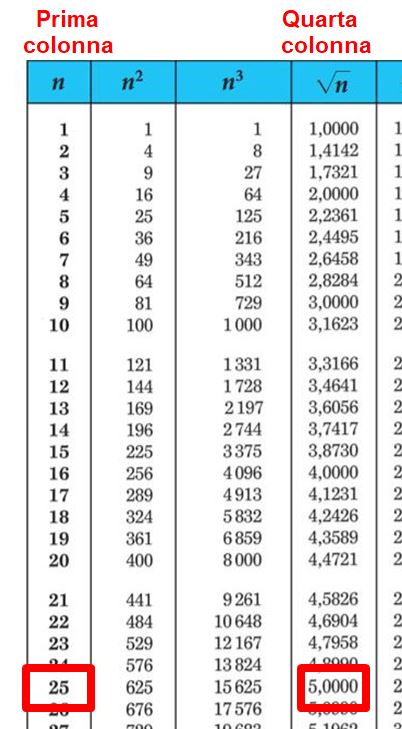
Il risultato che leggiamo è:
5,0000
Le tavole forniscono il risultato approssimato alla quarta cifra decimale (vuol dire che dopo la virgola ci sono 4 cifre). Questo è necessario perchè i risultati delle radici quadrate sono quasi sempre numeri decimali. Solo raramente i risultati sono numeri naturali. In questo caso le 4 cifre decimali sono quattro zeri. Ma noi sappiamo dalle scuole elementari che se dopo la virgola abbiamo solo zeri, questi zeri sono senza valore e non si scrivono.
5,0000 = 5
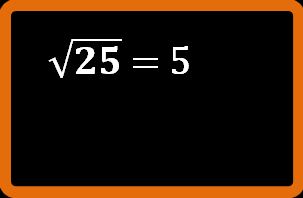
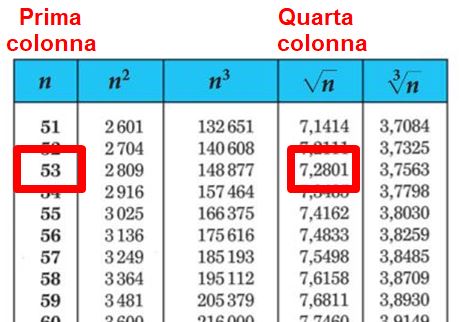
Facciamo un altro esempio. Vogliamo sapere la radice quadrata di 53. Quello che dobbiamo fare è andare a cercare il 53 nella prima colonna. Il risultato lo troveremo nella quarta colonna.
Il risultato che stiamo cercando è 7,2801.
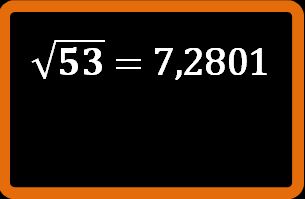
La prof poi, probabilmente, vi assegnerà un esercizio in cui si dovrà approssimare alla seconda cifra decimale oppure alla terza, ma questo è un altro discorso.
quinta colonna
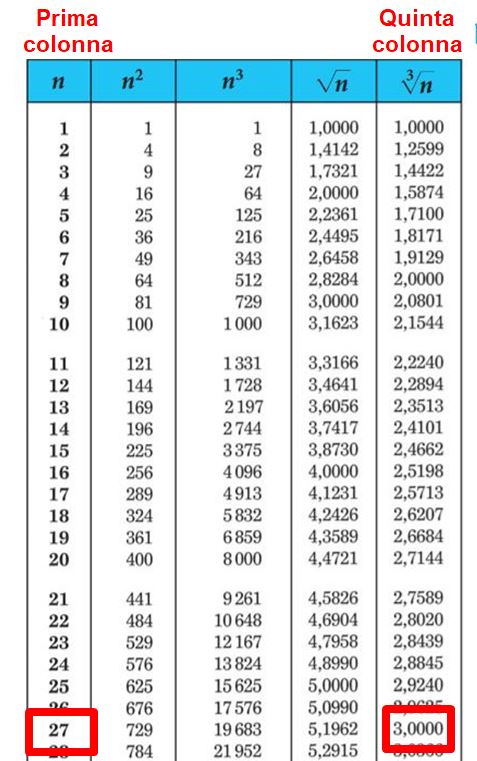
Andiamo avanti e cerchiamo di capire a cosa servono la terza, la quarta e la quinta colonna delle tavole numeriche. Nella quinta colonna troviamo la radice cubica che raramente si studia alle scuole medie. Ma dato che ci siamo diciamo cos’è.
5 è la radice quadrata di 25 perchè: 5 · 5 = 25
Seguendo un ragionamento molto simile si ha che:
3 è la radice cubica di 27 perchè: 3 · 3 · 3 = 27.
Radice quadrata di numeri maggiori di 1000
Nelle tavole troviamo la radice quadrata dei numeri da 1 a 1000.

ma con un piccolo ragionamento possiamo anche ricavare la radice quadrata di numeri più grandi di 1000. Vediamo come si fa.
Partiamo un po’ da lontano. Proviamo a determinare usando le tavole la radice quadrata di 100. Possiamo percorrere due strade.
La prima strada è questa: cerco il 100 nella prima colonna e la radice quadrata nella quarta colonna.
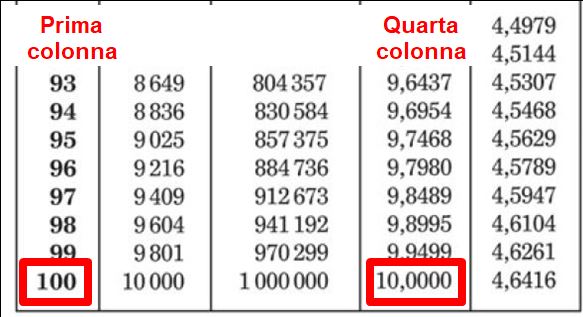
E fin qui niente di nuovo.
Vediamo ora la seconda strada. Posso cercare il 100 nella seconda colonna e leggere la sua radice quadrata nella prima colonna.
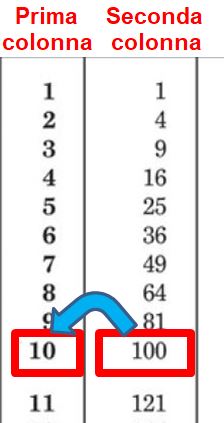
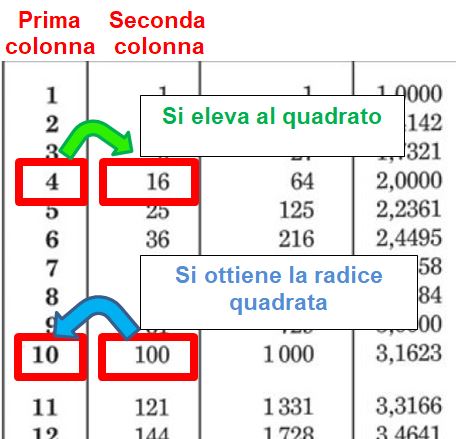
Cerchiamo di capire perchè. Ricordiamo che nella seconda colonna troviamo il quadrato del numero naturale presente nella prima colonna.
Quindi in altre parole, passando dalla prima alla seconda colonna, passiamo dal numero naturale al suo quadrato.
Facendo il percorso inverso (cioè dalla seconda colonna alla prima), eseguiamo l’operazione inversa. L’operazione inversa dell’elevamento al quadrato è la radice quadrata. Quindi passando dalla seconda colonna alla prima otteniamo la radice quadrata.
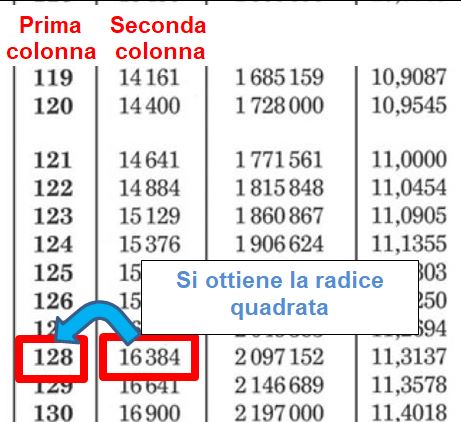
In questo modo è possibile, per esempio, ricavare la radice quadrata di 16384 = 128.
I numeri primi dall’ 1 a 10000
A pagina 13 e 14 delle tavole trovi i numeri primi da 1 a 10000. Ti saranno molto utili nella scomposizione in fattori primi o quando dovrai calcolare il minimo comune multiplo.
Se hai notato il primo numero primo non è il numero 1, ma il numero 2, che è anche l’unico numero primo pari.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati a quei lettori che segnaleranno eventuali errori presenti nell’articolo.