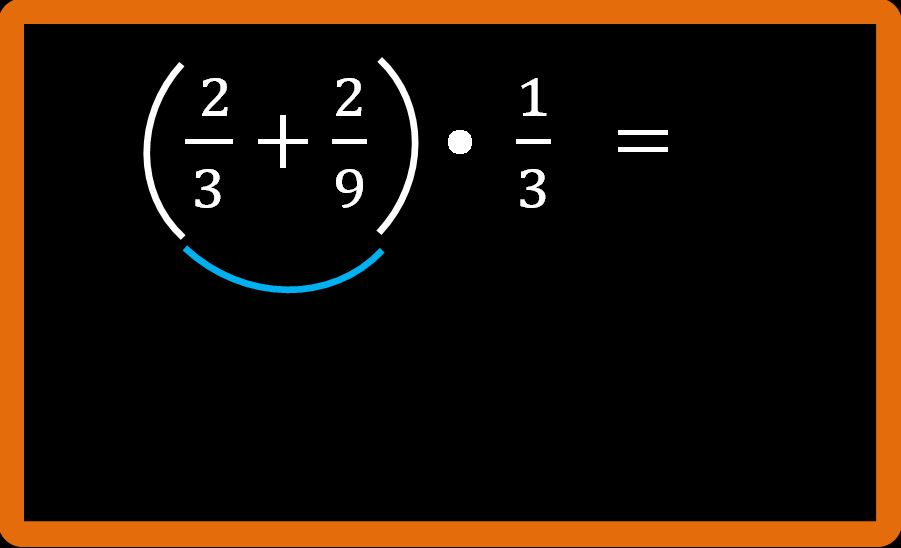Dopo avere visto una breve introduzione sulle espressioni con le frazioni, in questo articolo vedremo un esercizio svolto con le espressioni con le frazioni. Come abbiamo già detto ci sono delle precedenze che vanno rispettate. Sono solo poche regole da seguire, ma queste poche regole ti permetteranno di eseguire in modo corretto qualsiasi espressione. Non preoccuparti se all’inizio ti sembra di impiegare tanto tempo o se i primi esercizi non ti riescono. È normale, abbiamo iniziato tutti così. Non arrenderti e vai avanti.
Le precedenze da rispettare
- Ridurre ai minimi termini (quando possibile);
- Operazioni dentro le parentesi (tonde, quadre e graffe);
- Moltiplicazioni e divisioni;
- Addizioni e sottrazioni procedendo da sinistra verso destra.
Primo esercizio
Cominciamo con un esercizio piuttosto semplice. Proviamo a risolvere l’espressione che leggi nella lavagna sotto.
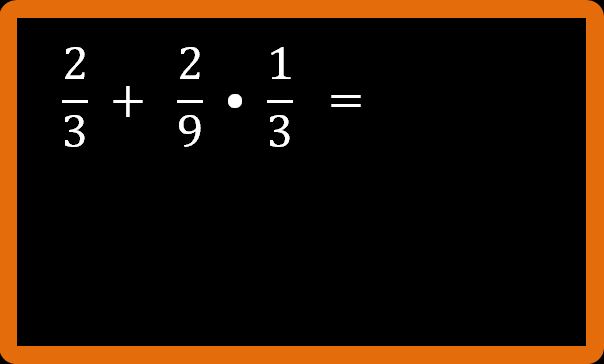
Prima di cominciare a eseguire i calcoli, osserviamo l’espressione che dobbiamo risolvere. Sono presenti un’ addizione e una moltiplicazione. Andiamo a guardare le precedenze. Non si può ridurre ai minimi termini nessuna frazione e non ci sono parentesi. La precedenza che dobbiamo rispettare è :
la moltiplicazione va eseguita prima dell’ addizione.
Per essere sicuri di fare bene, disegniamo un piccolo archetto sotto le frazioni interessate dalla moltiplicazione. In altre parole tracciamo un archetto sotto i fattori della moltiplicazione.
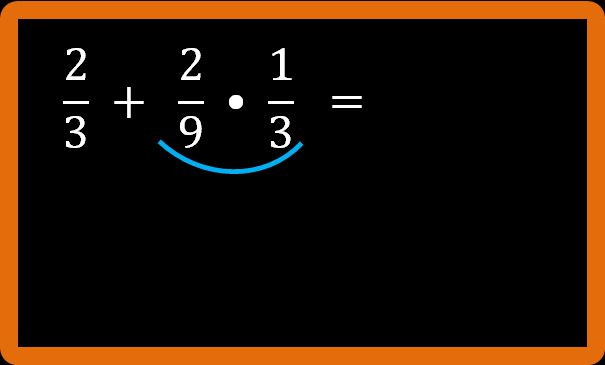
Non è possibile semplificare in croce, quindi possiamo ora andare a eseguire la moltiplicazione tra frazioni che si esegue: numeratore per numeratore (2 · 1) e denominatore per denominatore (9 · 3).
Io preferisco andare a capo dopo ogni passaggio. È una questione di ordine. Se vai a capo capisci quando termina ogni passaggio, in questo modo se commetti qualche errore è più facile accorgersene e rimediare. Quindi a costo di sprecare qualche foglio in più del tuo quaderno ti consiglio caldamente di andare a capo. Ricorda: si finisce il passaggio con un uguale ‘=’ e si comincia il nuovo passaggio con un ‘=’.
Riscriviamo la prima frazione, cioè due terzi e poi scriviamo il risultato della moltiplicazione, cioè due ventisettesimi.
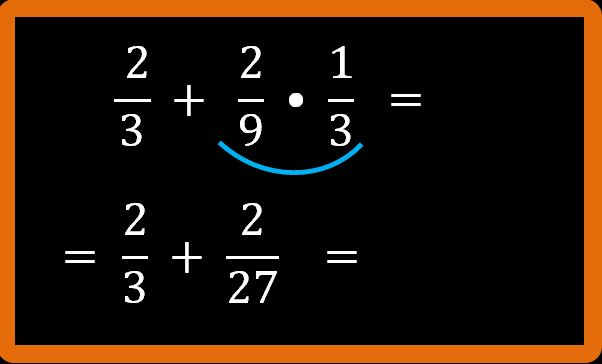
Proseguiamo con il nostro esercizio con le espressioni con le frazioni. Quello che dobbiamo fare è una addizione tra frazioni con denominatore diverso. Andrebbe calcolato il minimo comune multiplo tra i denominatori. Ma guardiamo con attenzione. I denominatori sono 3 e 27.
Il 27 è un multiplo di 3 (ricordando la tabellina del tre: 3 · 9 = 27). Quando calcoliamo l’ m.c.m. tra due numeri, e uno dei due numeri è multiplo dell’altro, allora possiamo dire anche che è anche il minimo comune multiplo.
Se non ti ricordi questa regola o non ti accorgi che 27 è multiplo di 3, poco male. Procedi normalmente con la scomposizione in fattori primi e il calcolo dell’ m.c.m..

Calcolato l’m.c.m.m possiamo proseguire con l’espressione. Il minimo comune multiplo diventa il denominatore comune della frazione:
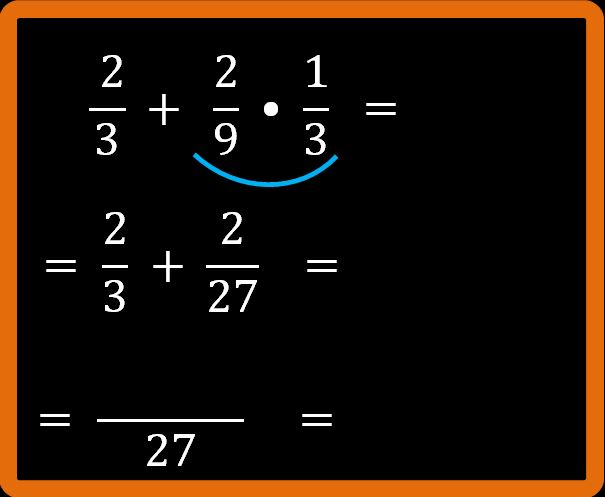
Procediamo come abbiamo imparato a fare quando abbiamo parlato di somma tra frazioni con denominatore diverso.
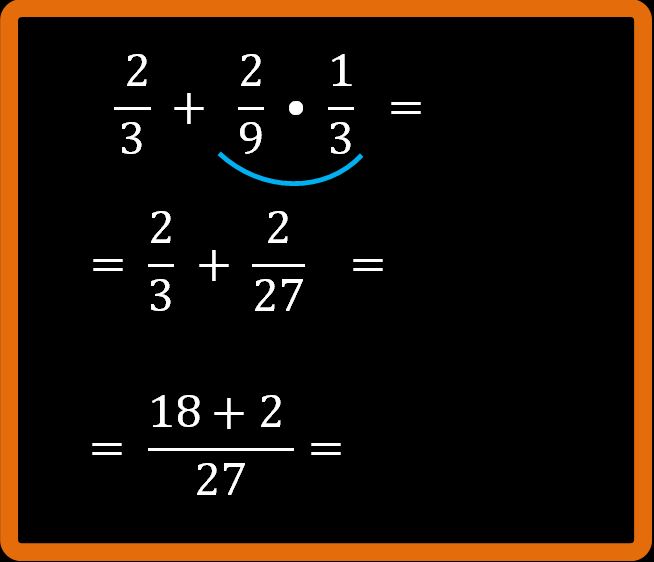
Adesso dobbiamo eseguire l’addizione al numeratore:

Siamo arrivati alla frazione 20 su 27. Non è possibile ridurre ai minimi termini, quindi abbiamo concluso. Venti ventisettesimi è il risultato che stavamo cercando. Ben fatto.
Le tavole numeriche sono uno strumento molto utile. Puoi usarle in classe e puoi anche usarle anche durante una verifica. Di solito si trovano all’interno del primo volume del libro di matematica, però può capitare di perderle (in realtà sono la prima cosa che gli studenti perdono). Se poi hai comprato il libro di seconda mano è quasi impossibile che tu le abbia trovate. Niente paura. Facendo click su questo link della Casa Editrice Zanichelli puoi consultare le tavole. Le puoi anche scaricare sul tuo pc come file pdf per poterle consultare off-line e averle sempre a disposizione. Se non ti ricordi come si scarica un file puoi seguire le istruzioni che trovi alla fine di questo mio articolo.
Se hai dubbi o vuoi segnalare un errorre puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori presenti nelle nostre pagine.