In un articolo precedente abbiamo iniziato a parlare della potenza di una frazione. Avrai notato che la frazione che viene elevata a potenza è contenuta all’interno di parentesi tonde. In questo articolo vedremo in particolare la potenza di una frazione e l’importanza delle parentesi.
Indice
Iscriviti al mio canale YouTube
Esempio 1
Iniziamo con questo esempio: tre quarti elevato alla seconda (si può anche leggere 3 su 4 tutto elevato alla seconda):
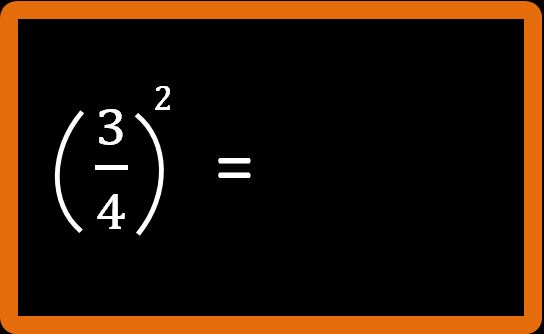
Le parentesi indicano che è tutta la frazione a essere elevata alla seconda, cioè sia il numeratore sia il denominatore. Calcoliamo questa frazione. Ti ricordo che tre quarti elevato alla seconda vuol dire tre quarti per tre quarti. Il significato della potenza è proprio questo.
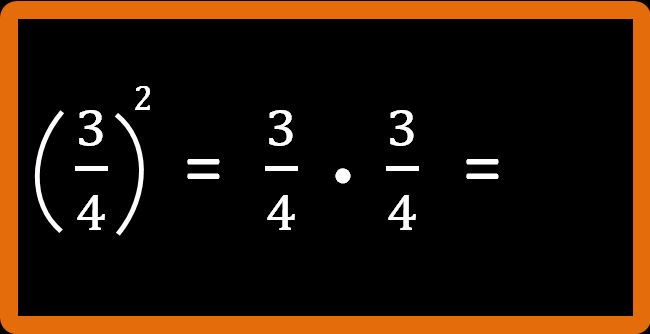
È una moltiplicazione tra frazioni che sappiamo eseguire. Non è possibile semplificare in croce, per cui quello che dobbiamo fare è moltiplicare:
- il numeratore della prima frazione per il numeratore della seconda, cioè 3 • 3 = 9 e
- il denominatore della prima frazione per il denominatore della seconda, cioè 4 • 4 = 16.
Quello che otteniamo allora è:
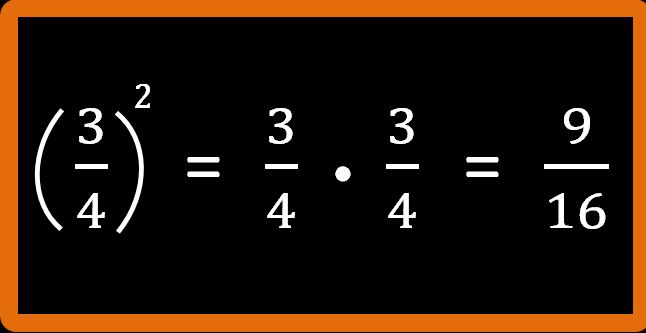
Il risultato che otteniamo è nove sedicesimi. Esercizio concluso.
Esempio 2
Proviamo ora a scrivere la stessa frazione con lo stesso esponente, ma senza parentesi:
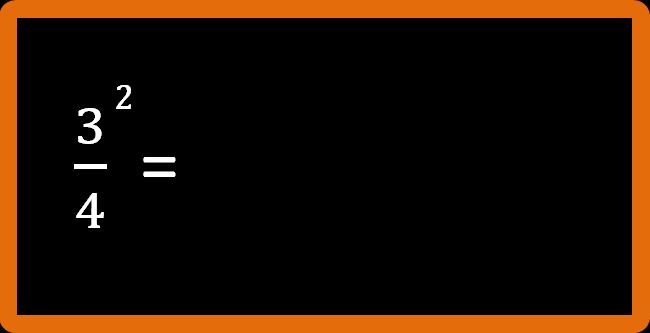
Proviamo a leggere questa frazione. Facciamo però molta attenzione. In questo caso l’esponente 2 si riferisce solo al numeratore e non al denominatore. Quindi il modo corretto di leggere questa frazione è:
3 elevato alla seconda fratto 4 oppure 3 elevato 2 su 4.
Leggere tre quarti elevato alla seconda è scorretto perchè non è tutta la frazione a essere elevata alla seconda, ma solo il numeratore.
Vediamo come si esegue questo calcolo. Al numeratore abbiamo una potenza che va sviluppata:
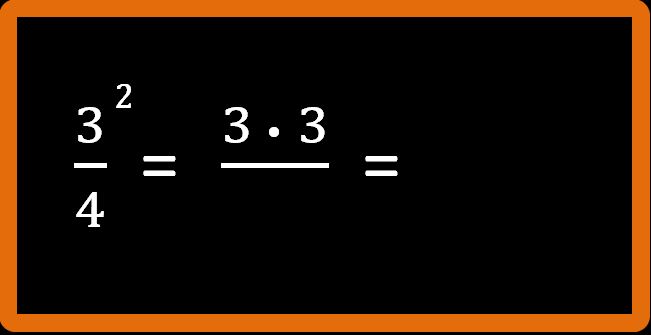
Il denominatore si può riscrivere perchè non c’è nessuna operazione da compiere.

Non ci rimane che eseguire i calcoli al numeratore (io sto eseguendo tutti i passaggi, ma se tu ti ricordi che 32 = 9 puoi anche scriverlo direttamente).
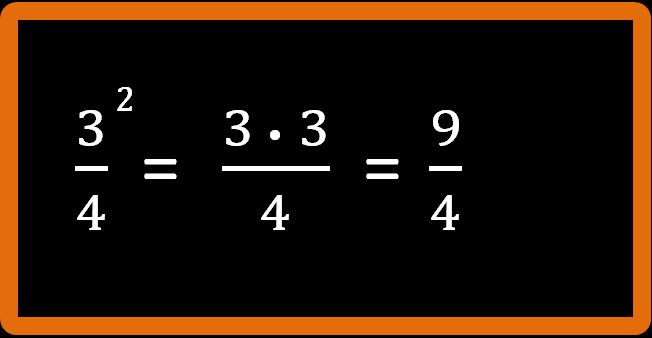
Il risultato che otteniamo è nove quarti, diverso da quello ottenuto nell’esempio 1 che era 9 su 16. Questo esempio ci fa capire l’importanza delle parentesi nella potenza di una frazione.
Esempio 3
Facciamo ancora altri due esempi con e senza parentesi.
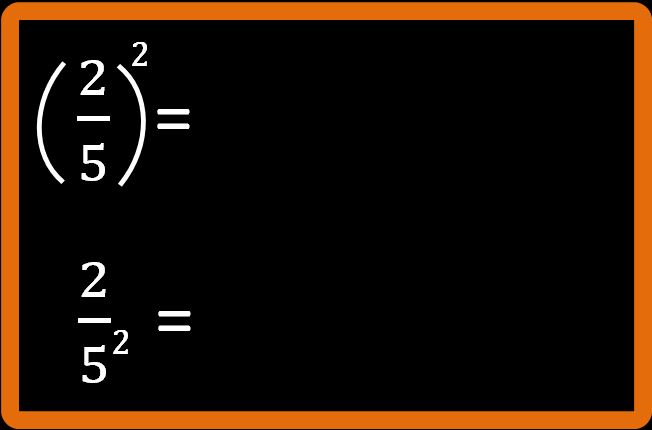
Abbiamo due frazioni diverse. Prova a leggerle. Attenzione alle parentesi.
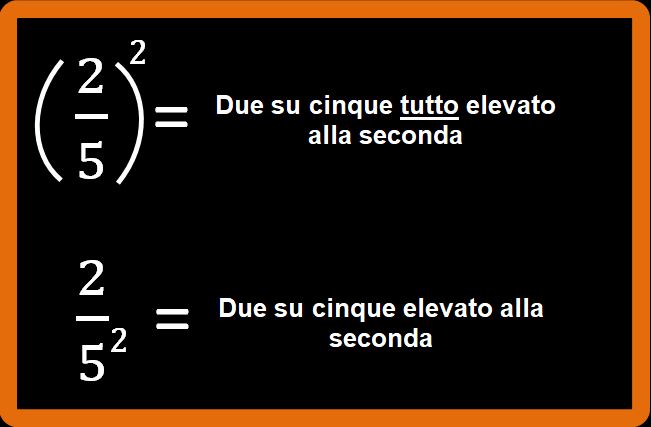
È la parola tutto che fa la differenza, infatti nella prima frazione ci fa capire che è proprio tutta la frazione a essere elevata alla seconda (cioè a 2). Invece nella seconda frazione è solo il denominatore a essere elevato alla seconda.
Andiamo a calcolare le nostre frazioni eseguendo i passaggi che abbiamo già visto negli esempi precedenti.
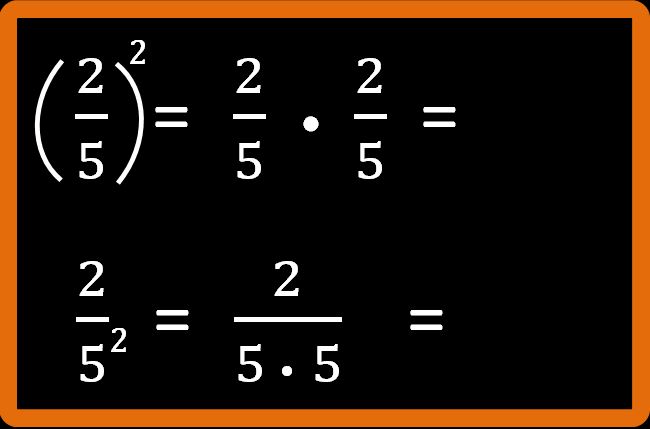
Quello che otteniamo è:

Otteniamo due risultati diversi perchè sono due frazioni diverse. Quindi facciamo molta attenzione alla presenza delle parentesi. Buon lavoro.
Esercizi
Adesso prova da solo a eseguire i tre esercizi che puoi leggere alla lavagna. Hai tutti gli strumenti e le conoscenze necessarie per eseguirli in modo corretto. Non avere premura, lavora con calma e non ti preoccupare se sbagli, nessuno verrà a rimproverarti. Alla fine dell’articolo trovi alcune soluzioni errate. Non ti do le soluzioni giuste e ti spiego perchè. Quando andrai a fare la verifica di matematica non avrai le soluzioni, non ci sarà nessuno a dirti se quelo che stai scrivendo è giusto o sbagliato. Devi acquisire sicurezza nei tuoi mezzi. Quindi armati di coraggio e prova. Se proprio non riesci a farne a meno puoi richiedere i risultati corretti alla casella mail che trovi sotto.

Esercizi in pdf
Se vuoi puoi scaricare e stampare gli esercizi in formato pdf che vedi sotto.
![]() Potenza di una frazione – Esercizi.pdf
Potenza di una frazione – Esercizi.pdf
![]() Potenza di una frazione – Esercizi 2.pdf
Potenza di una frazione – Esercizi 2.pdf
A questo link della Casa Editrice Zanichelli trovi le tavole numeriche. Puoi consultarle o scaricarle come file pdf per averle sempre a disposizione anche quando sei off-line.
Se hai dubbi o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori.
Alcune risoluzioni sbagliate