In un articolo precedente abbiamo visto cosa sono le frazioni e cosa indicano il numeratore e il denominatore. Se non lo ricordi sarebbe meglio andare a dare un’occhiata. In questo articolo invece cercheremo di capire quali sono le frazioni equivalenti.
Se non l’hai ancora fatto, iscriviti al mio canale Youtube 🙂.
Indice
- Cosa vuol dire equivalente
- Primo esempio
- Secondo esempio
- Passare da una frazione a un’altra frazione equivalente
- Ridurre ai minimi termini una frazione
- Fattore di riduzione e fattore di espansione di una frazione
- Esercizi in pdf
Cosa vuol dire “equivalente”
La parola equivalente vuol dire: ‘che ha lo stesso valore’. Facciamo un esempio aiutandoci con la geometria. Avrai sicuramente studiato che la formula per calcolare l’area del rettangolo è: base x altezza.

- dove A è la misura dell’area,
- B è la misura della base e
- h è la misura dell’altezza.
Se hai a disposizione un quaderno a quadretti disegna due rettangoli come quelli sotto. Nel primo rettangolo la base è lunga 3 quadretti e l’altezza misura 2. Invece nel secondo rettangolo la base misura 6 quadretti e l’altezza misura 1.
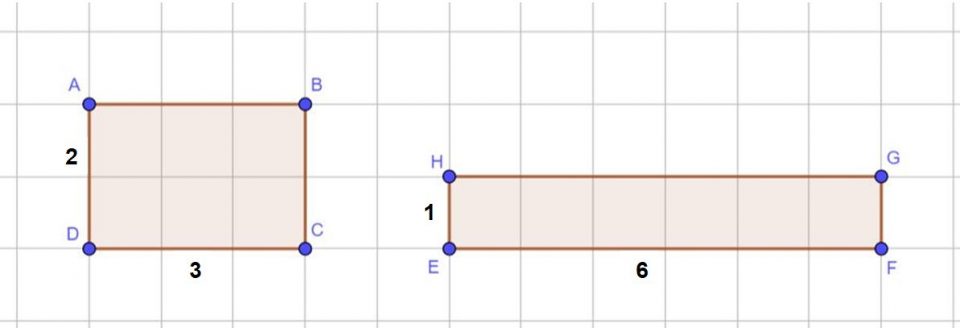
Andiamo a calcolare l’area dei due rettangoli (usando la formula che abbiamo letto sopra).
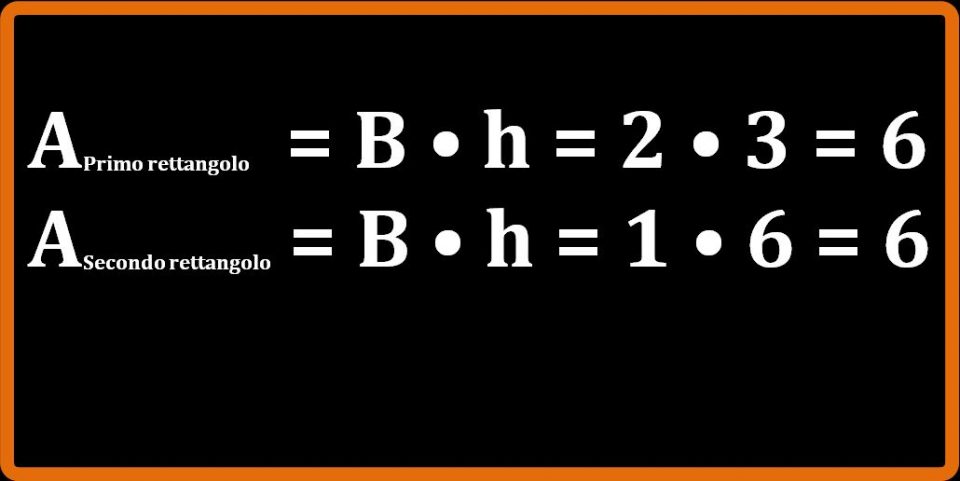
Vediamo che anche se i due rettangoli sono diversi, hanno le stesse aree. Si dice che i due rettangoli sono equivalenti, cioè le loro aree hanno lo stesso valore.

Esempio 1 – Frazioni equivalenti: le tavolette di cioccolato
Adesso che abbiamo spiegato cosa vuol dire equivalente cominciamo a lavorare con le frazioni.
Disegniamo due rettangoli come quelli che vedi sotto. Con un po’ di fantasia immaginiamo che siano due tavolette di cioccolato. La prima tavoletta è divisa in sei parti uguali, invece la seconda tavoletta è divisa in due parti uguali (è importante sottolineare che devono essere parti uguali altrimenti non è possibile usare le frazioni. Ricorda frazionare vuol dire dividere in parti uguali).
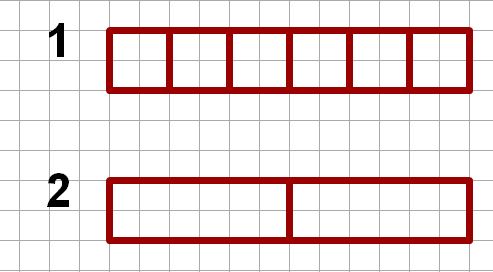
Della prima tavoletta ne mangio tre parti, che vado a colorare. La frazione che rappresenta le parti che ho mangiato è 3 su 6 oppure tre sesti. (Ripetiamo, l’intero era diviso in 6 parti e noi ne consideriamo 3, per cui 3 su 6.)
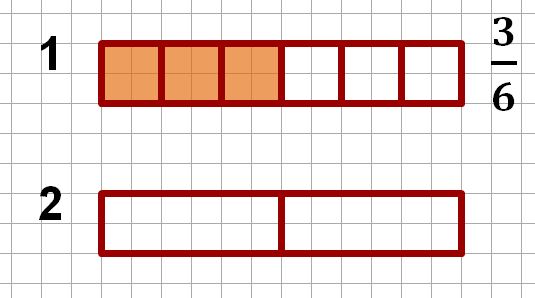
Della seconda tavoletta, invece mangio solo una parte, e vado a colorare anche questa. La frazione che indica la parte che mangio è 1 su 2 che si può anche leggere un mezzo.
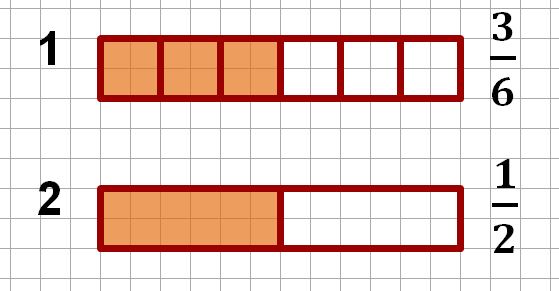
Fantastico. Abbiamo scritto in modo corretto le due frazioni che rappresentano le parti mangiate. Ma nella realtà dei fatti io ho mangiato la stessa quantità di cioccolato. Ho mangiato metà tavoletta.
Ce ne possiamo anche rendere conto, andando a contare i quadratini. Infatti i quadratini colorati sono 12 sia nella prima tavoletta, sia nella seconda tavoletta.
Allora possiamo dire che le frazioni tre sesti e un mezzo sono equivalenti perchè rappresentano la stessa quantità.

Tutto quello che stiamo dicendo ti sarà utile quando studierai le addizioni e le sottrazioni tra frazioni. Per il momento facciamo un altro esempio per essere sicuri di capire bene le frazioni equivalenti.
Esempio 2 – Frazioni equivalenti: le pizze
Molto bene, facciamo un altro esempio aiutandoci sempre con qualcosa di pratico. Immaginiamo di essere in pizzeria con i nostri compagni di classe. Due dei tuoi compagni: Lorenzo e Martina prendono la stessa pizza, ma Lorenzo la divide in 4 tranci uguali. Invece Martina la divide in 8 pezzi uguali.
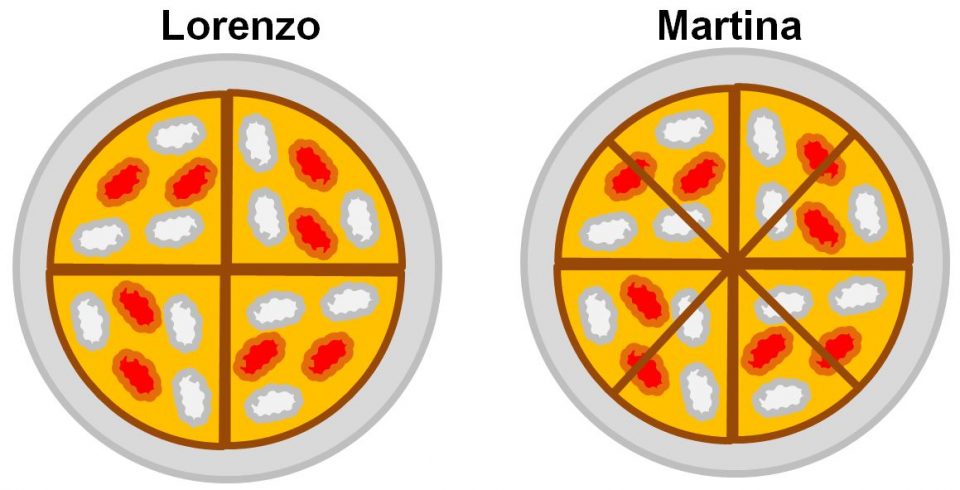
Nessuno dei due riesce a mangiare tutta la pizza. La situazione a fine serata è quella che vedi sotto.
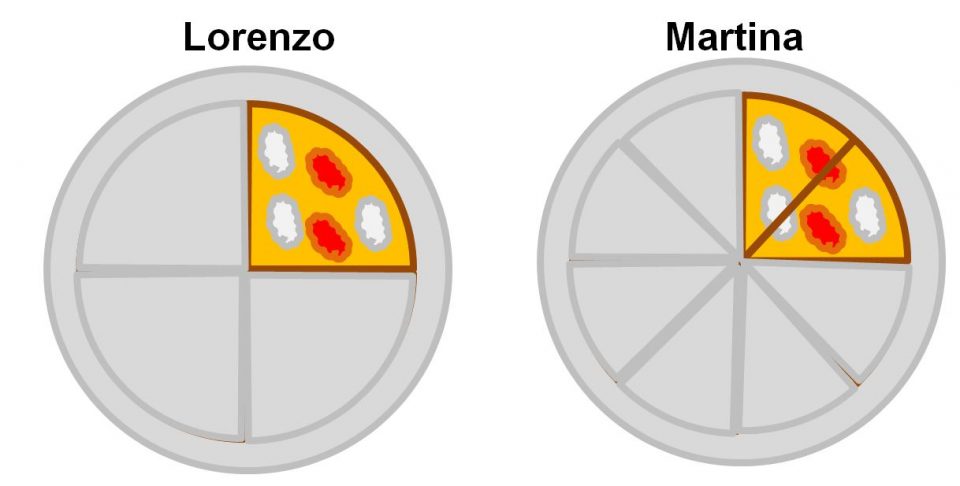
Rappresentiamo ora con una frazione la parte di pizza che Lorenzo non ha mangiato.

E con un’altra frazione la parte di pizza non mangiata da Martina.

Riassumendo abbiamo che:

Le frazioni che rappresentano le parti di pizza che Lorenzo e Martina non hanno mangiato, sono diverse, infatti hanno numeratori e denominatori diversi.
Ma se guardiamo con attenzione i due piatti a fine serata, ci rendiamo conto che, nella realtà dei fatti, hanno mangiato la stessa quantità di pizza. Solo che quella di Martina era tagliata in modo diverso.
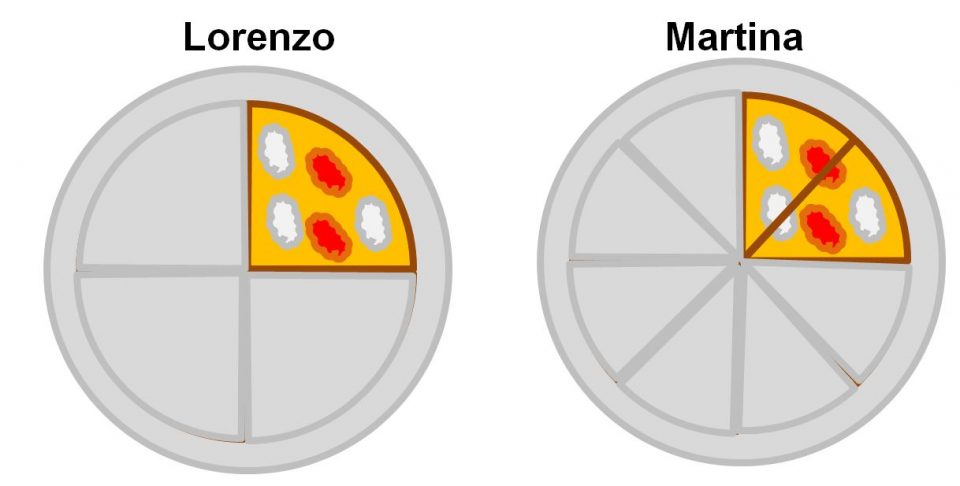
Allora possiamo concludere che le due frazioni un quarto e due ottavi rappresentano la stessa quantità, in altre parole hanno lo stesso valore, cioè sono frazioni equivalenti.

Passare da una frazione a un’altra frazione equivalente
Ok, adesso che abbiamo capito cosa sono le frazioni equivalenti, dobbiamo capire come si ottiene una frazione equivalente a partire da un’altra frazione qualsiasi. Non ti preoccupare, è molto semplice.
Partiamo subito con un esercizio numerico. Prendiamo in considerazione le frazioni dell’esempio precedente (quello delle pizze). Come possiamo passare matematicamente (quindi usando le operazioni matematiche) da un quarto a due ottavi? Dobbiamo moltiplicare numeratore e denominatore per lo stesso numero naturale. Procediamo passo passo. (Se non ti ricordi quali sono i numeri naturali, potresti dare un’occhiata al mio articolo).
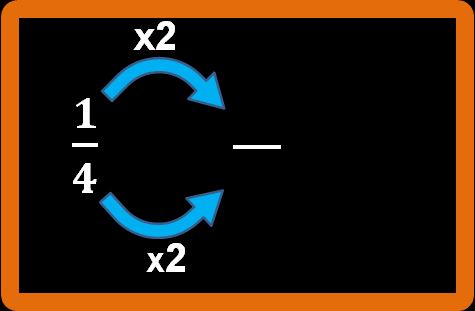
Il numeratore della nostra frazione è 1. L’operazione che dobbiamo eseguire è:
1 · 2 = 2
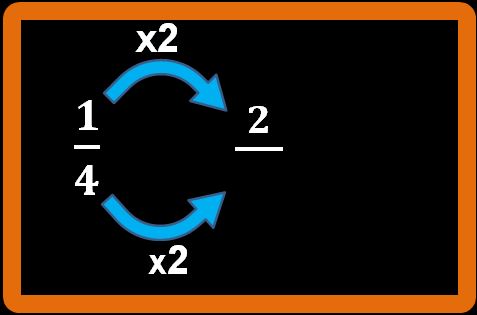
Il denominatore è 4. L’operazione che dobbiamo eseguire è:
4 · 2 = 8
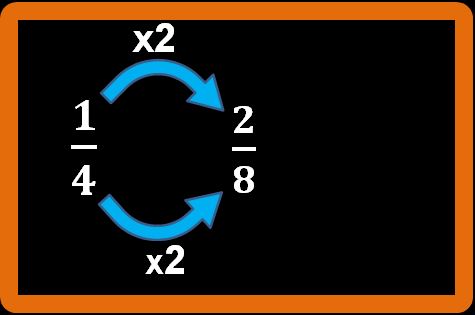
Abbiamo ottenuto la frazione due ottavi che è equivalente alla frazione un quarto.
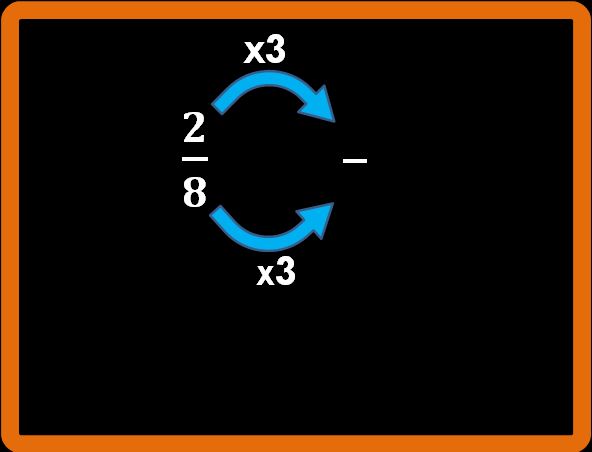
Partendo da due ottavi, possiamo ottenere altre frazioni equivalenti. Per esempio possiamo moltiplicare numeratore (2) e denominatore (8) per 3.
2 · 3 = 6; 8 · 3 = 24;
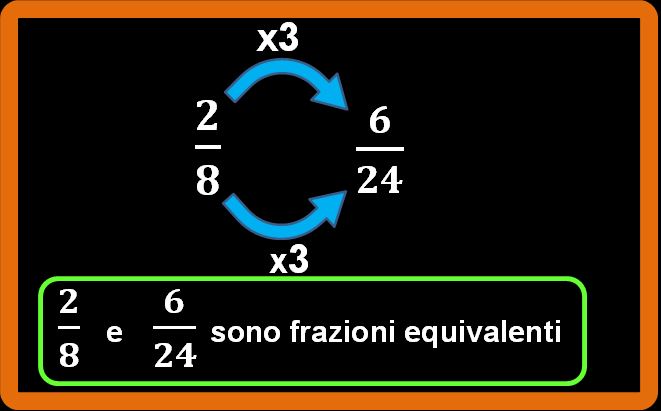
Per ottenere frazioni equivalenti è anche possibile dividere numeratore e denominatore per lo stesso numero. Per esempio:
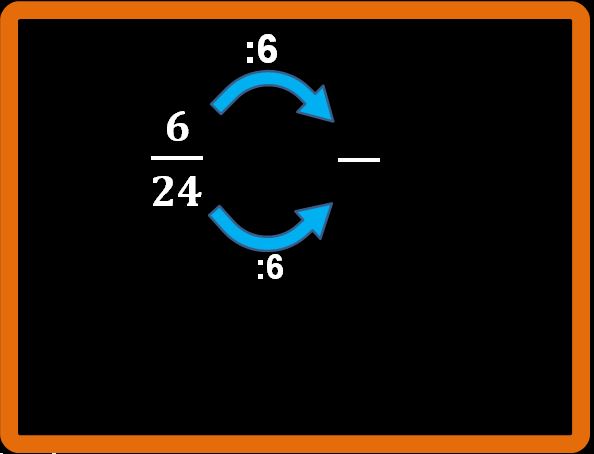
Le operazioni che dobbiamo fare sono per il numeratore:
6 : 6 = 1
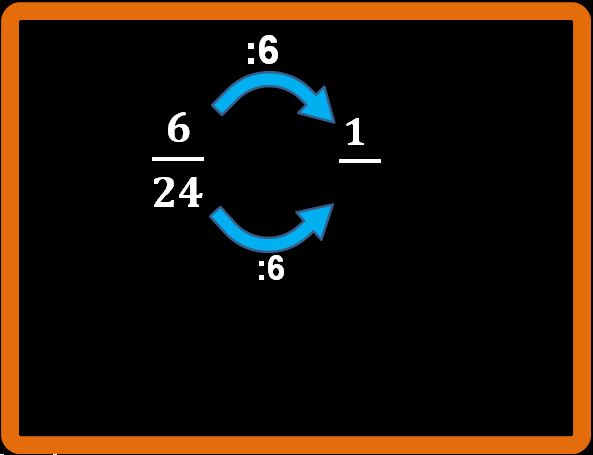
Invece per ottenere il denominatore della frazione equivalente dobbiamo eseguire la divisione:
24 : 6 = 4
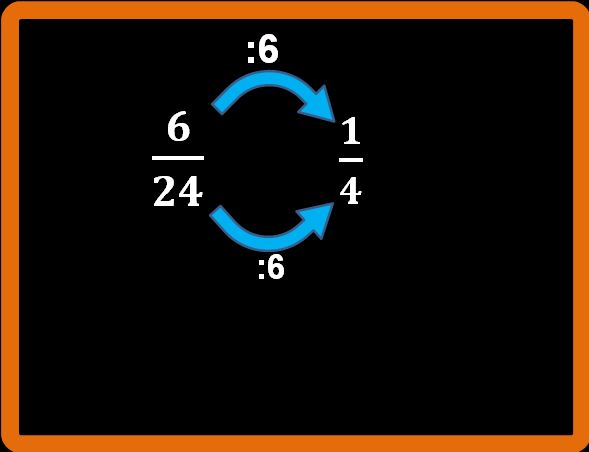
Abbiamo ottenuto che
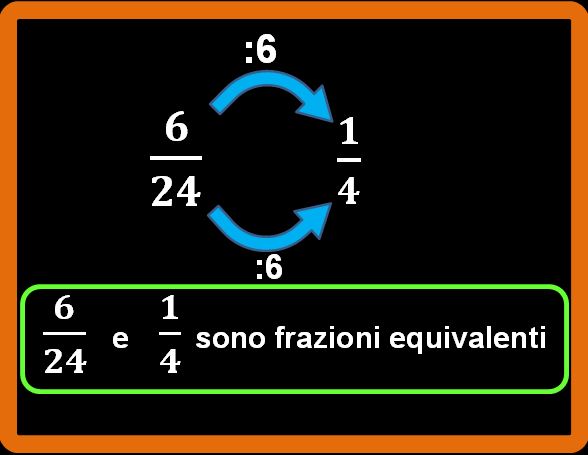
Tagliare una pizza in 24 pezzi è difficile, per cui avere un modello per capire questa equivalenza è poco agevole. Ma se ci ricordiamo il significato di frazione (la frazione è una divisione scritta in modo diverso), possiamo verificare che 6 su 24 e 1 su 4 sono effettivamente equivalenti.
Puoi usare una qualsiasi calcolatrice ed eseguire la divisione 6 : 24 = 0,25.
E poi eseguire la divisione 1 : 4 = 0,25.
Come vedi la calcolatrice restituisce lo stesso risultato, questo vuol dire che le due frazioni sono equivalenti.
Possiamo adesso enunciare la regola generale. “Per ottenere una frazione equivalente a un’altra frazione, si devono moltiplicare, o dividere, il numeratore e il denominatore della frazione di partenza per lo stesso numero naturale”.
Il procedimento tramite il quale si dividono il numeratore e il denominatore di una frazione per lo stesso numero viene detto ‘semplificazione‘. La semplificazione permette di ridurre una frazione ai minimi termini. Se vuoi maggiori chiarimenti sulla semplificazione e sulla riduzione ai minini termini, puoi dare un’occhiata al mio articolo.
Fattore di espansione e fattore di riduzione
Per evitare di scrivere le frecce che portano da una frazione a un’altra, è stato inventato un modo più veloce. Si usa il fattore di riduzione oppure il fattore di espansione, a seconda dei casi. Per saperne di più puoi leggere il mio articolo che trovi cliccando qui.
Buon lavoro e ricorda, se ti impegni puoi riuscire in tutto.
Esercizi in pdf
Adesso sai cosa sono le frazioni equivalenti e possiedi gli strumenti per eseguire qualsiasi esercizio che riguarda questo argomento. Se vuoi metterti alla prova puoi provare a eseguire gli esercizi che trovi subito sotto nel file pdf. Lavora con calma, senza fretta, non è una gara di velocità. Non ti preoccuapre se sbagli. Sbagliare è normale. Quando avrai terminato tutti gli esercizi potrai confrontare i tuoi risultati ocn le soluzioni.
![]() Frazioni equivalenti – Esercizi.pdf
Frazioni equivalenti – Esercizi.pdf
Buon lavoro.
A questo link della Casa Editrice Zanichelli trovi le tavole numeriche, puoi consultarle oppure puoi scaricarle come file pdf per averle sempre a disposizione anche quando sei off-ine.
Se hai domande o voui segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grato ai lettori che segnaleranno eventuali errori presenti nell’articolo.