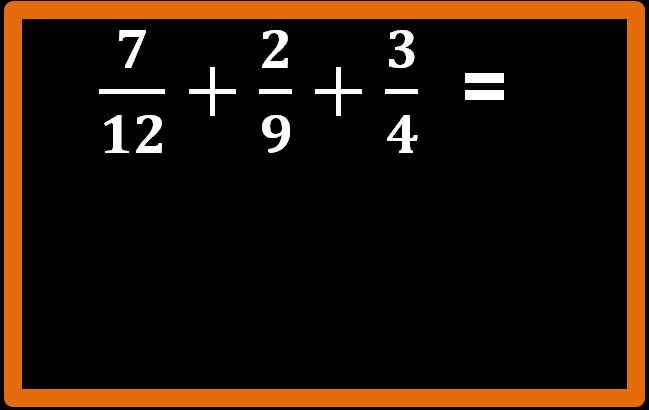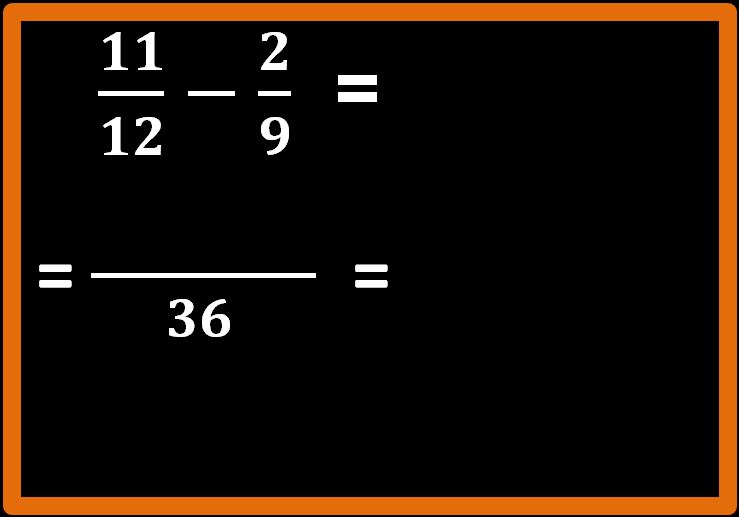Bene, hai imparato come si addizionano e si sottraggono le frazioni tra loro. Vediamo ora altri esempi di addizione e sottrazione tra frazioni. Supponiamo di voler sottrarre una frazione da un numero naturale. (Se non ti ricordi quali sono i numeri naturali potresti dare un’occhiata al mio articolo quali sono i numeri naturali.)
indice
esempio 1
Partiamo con un esempio. Ieri sera con i tuoi compagni di classe siete andati in pizzeria e hai ordinato la tua pizza preferita e l’hai tagliata in quattro parti uguali.
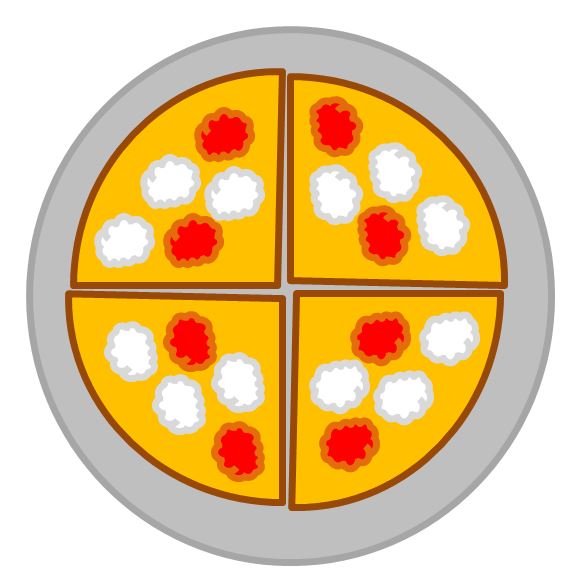
Ma non avevi molta fame e ne hai mangiato solo tre pezzi. Se vogliamo dirla in un altro modo hai mangiato tre pezzi su quattro. Abbiamo già usato una frazione 3 su 4, che si può leggere anche tre quarti.
Quanti pezzi ne sono avanzati? La risposta è molto semplice: ne è avanzato 1.
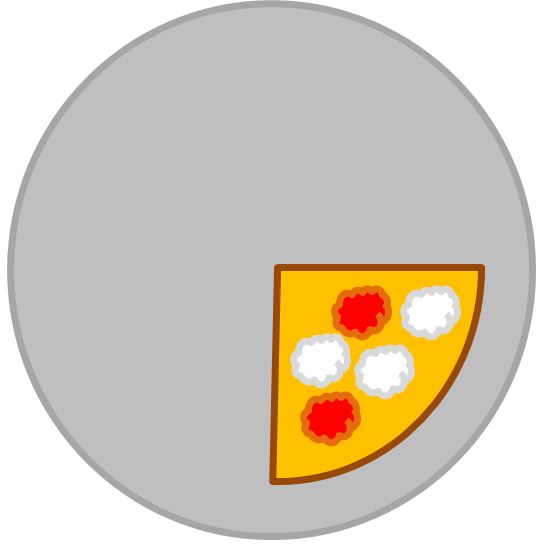
Tutto quello che abbiamo detto si può tradurre in linguaggio matematico (cioè con i numeri).
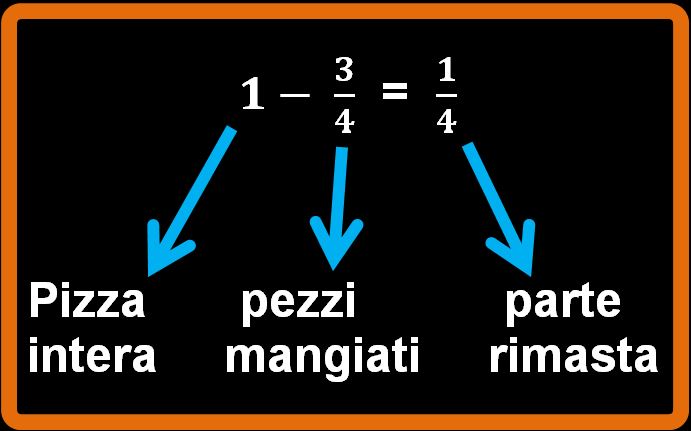
Se da una pizza intera togliamo tre quarti, quanto ne rimane? Ne rimane un quarto.
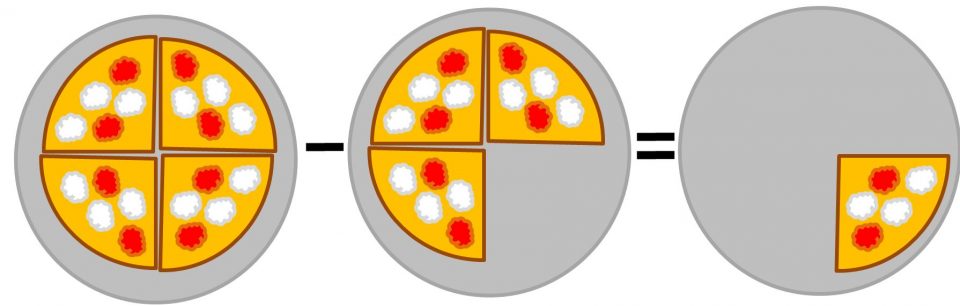
Passando ai numeri
Bene, con l’esempio della pizza è tutto chiaro. Ma se avessimo a che fare con questa sottrazione:
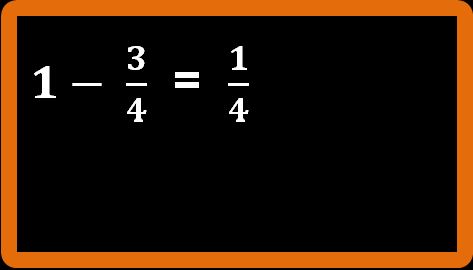
Come facciamo a ottenere il risultato esatto senza usare le pizze, ma usando dei calcoli? Vediamo come si procede facendo altri esempi di addizione e sottrazione tra frazioni.
esempio 2: Sottrazione e/o addizione tra un numero naturale e una frazione
Supponiamo di voler eseguire questa sottrazione:
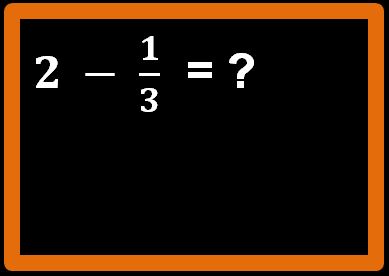
Potremmo aiutarci di nuovo con le pizze, ma è un procedimento lungo e non sempre conveniente.
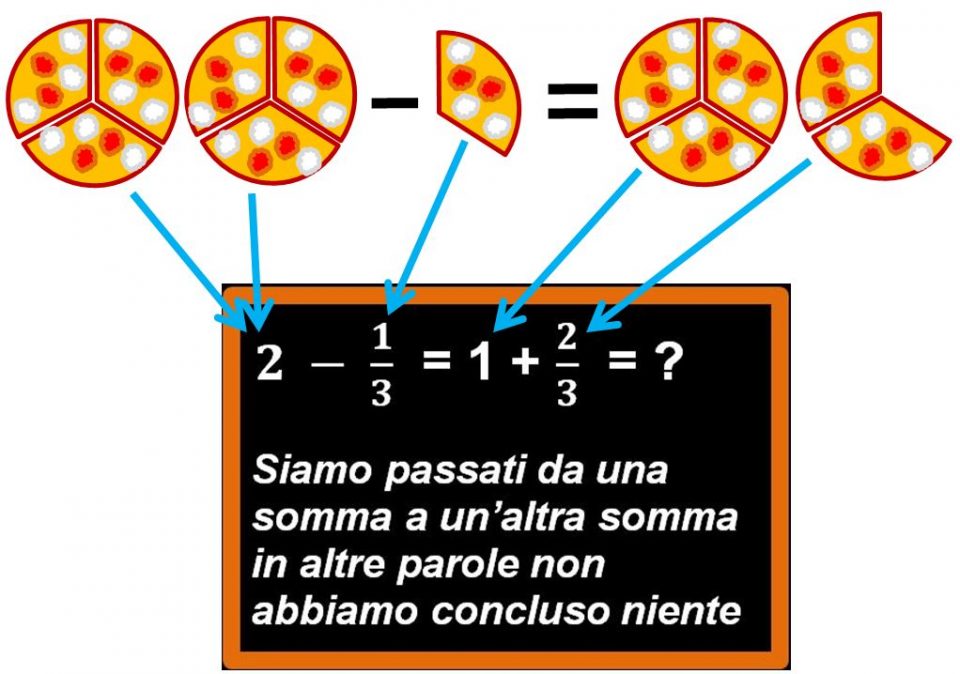
No. Non ci siamo. Dobbiamo trovare un altro metodo che sia più conveniente e più facile da eseguire.
Partiamo da questa premessa: ogni numero naturale, come per esempio il 2, può essere pensato come 2 fratto 1.
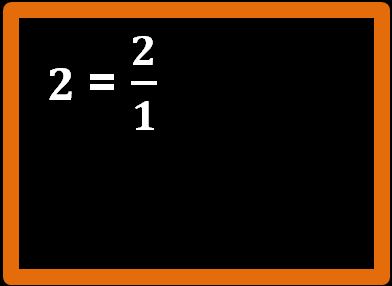
Allora possiamo riscrivere la nostra differenza di partenza nel modo che vedi sotto, sostituendo al numero 2 la frazione 2 fratto 1:
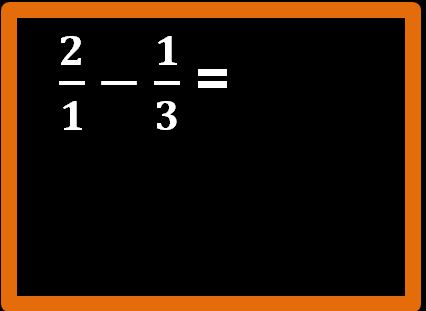
Questa è una differenza tra frazioni con denominatore diverso che noi sappiamo risolvere. Se non ti ricordi come si procede puoi dare una lettura al mio articolo somma tra frazioni con denominatore diverso.
Il primo passaggio da fare è determinare il minimo comune multiplo tra i denominatori, che nel nostro esempio sono i numeri 3 e 1.
Non è necessario scomporre in fattori primi perchè il 3 è un numero primo e il numero 1 non ha nessuna influenza nel calcolo dell’m.c.m. (ricorda che il numero 1 non è un numero primo).
Per essere proprio chiari chiari facciamo tutti i passaggi, ma solo questa volta.
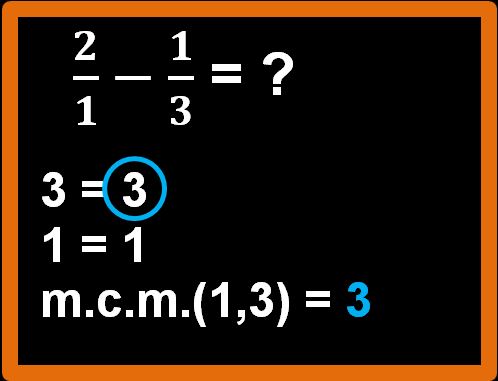
Il numero 1 non si considera nel calcolo dell’ m.c.m. perchè come sai che il numero 1 è l’elemento neutro della moltiplicazione. In altre parole vuol dire che : 5 x 1 = 5; 17 x 1 = 17.
Bene, abbiamo trovato l’m.c.m.. Tracciamo una linea di frazione sufficientemente lunga e mettiamo il nostro m.c.m. al denominatore.
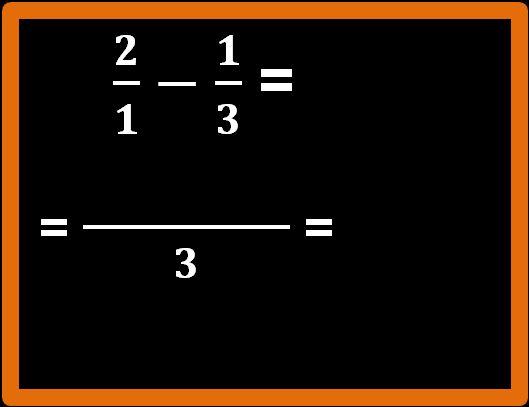
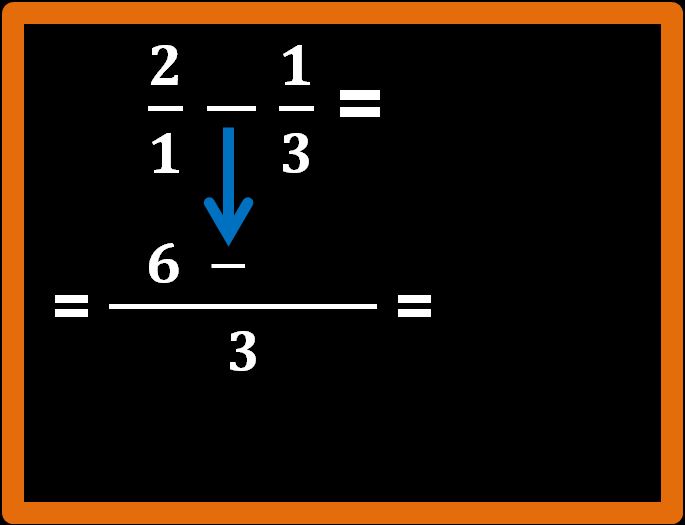
Adesso si procede come sappiamo: dividiamo l’m.c.m. per il denominatore della prima frazione e poi moltiplichiamo il risultato che abbiamo trovato per il numeratore della frazione:
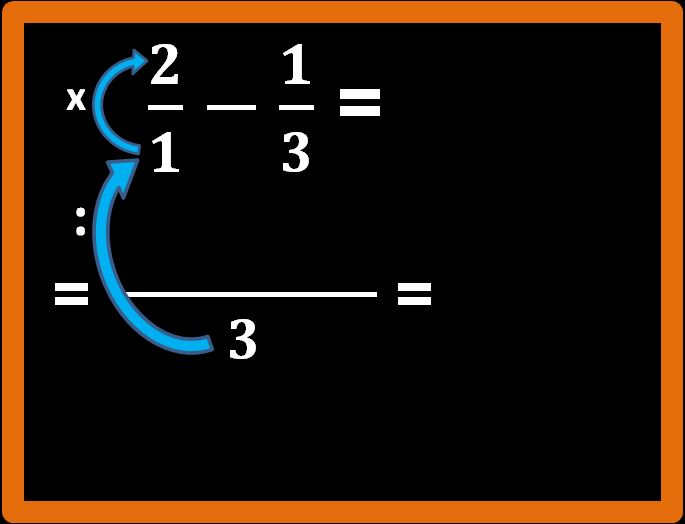
3 : 1 = 3; 3 · 2 = 6
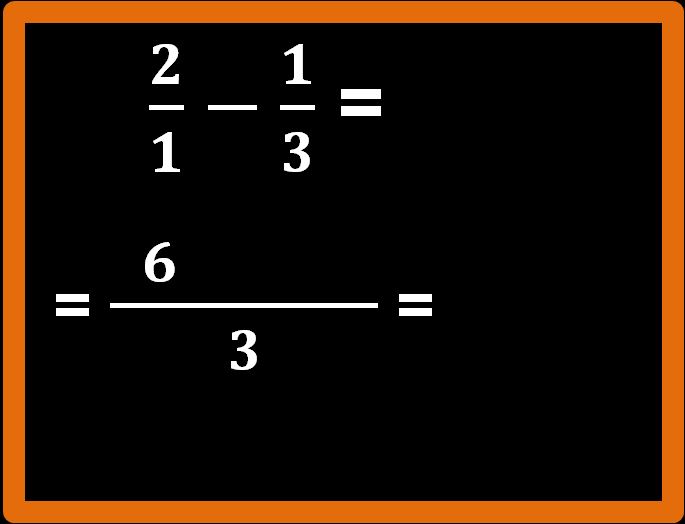
Facciamo attenzione al segno. Siamo partiti da una differenza (segno meno) e dobbiamo riscrivere il segno meno.
Adesso ripetiamo per la seconda frazione lo stesso procedimento seguito per la prima:
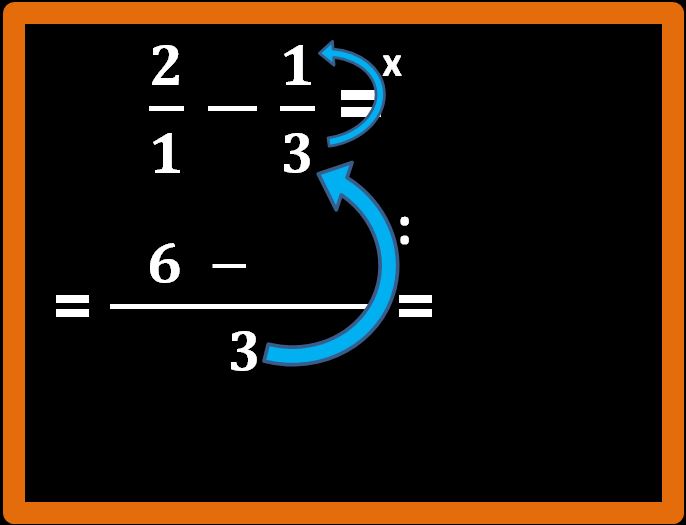
3 : 3 = 1; 1 · 1 = 1
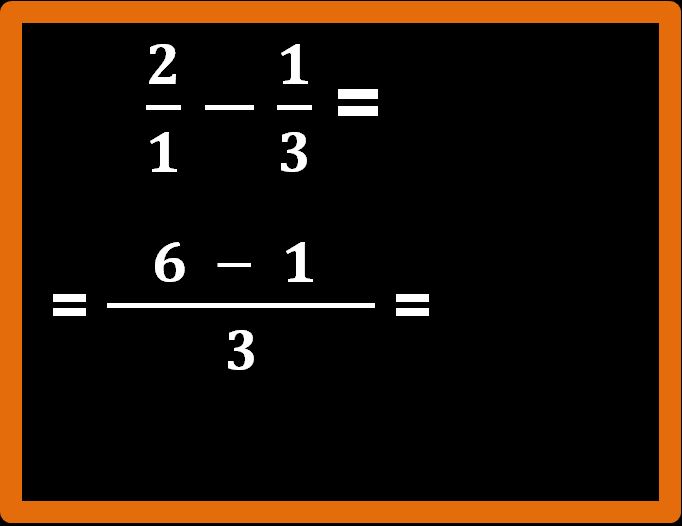
Adesso eseguiamo la differenza che troviamo al numeratore, cioè 6 – 1 = 5.
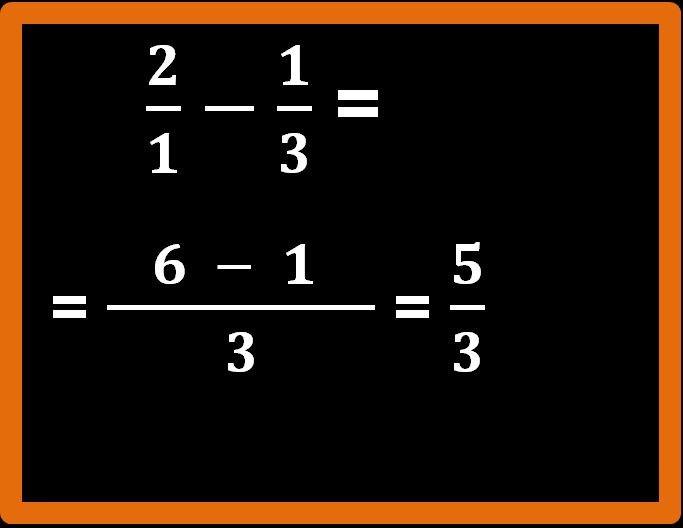
Abbiamo finito. Cinque terzi è il risultato che stavamo cercando. La frazione 5 su 3 è già ridotta ai minimi termini, per cui l’esercizio è concluso.
esempio 3
Andiamo avanti con altri esempi di addizione e sottrazione tra frazioni. Proviamo ora a calcolare la seguente espressione: due quindicesimi più 3 meno sette decimi:
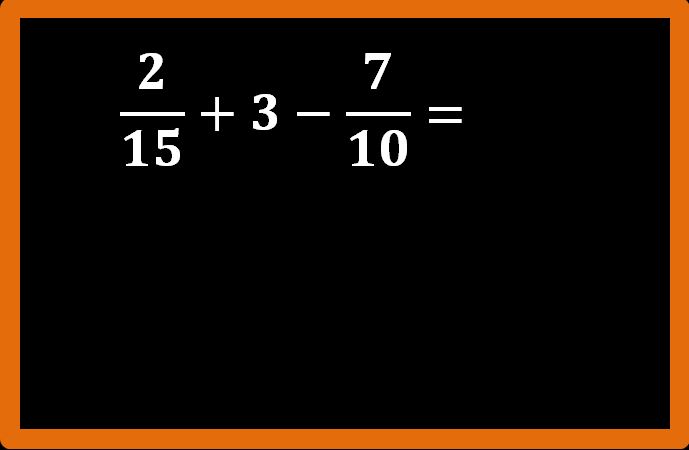
Abbiamo un’addizione e una sottrazione che coinvolge sia frazioni sia un numero naturale, il 3.
Niente paura, ricordiamoci che qualsiasi numero naturale può essere pensato come una frazione in cui il denominatoe è 1. Quindi il numero naturale 3 può essere pensato come 3 fratto 1.
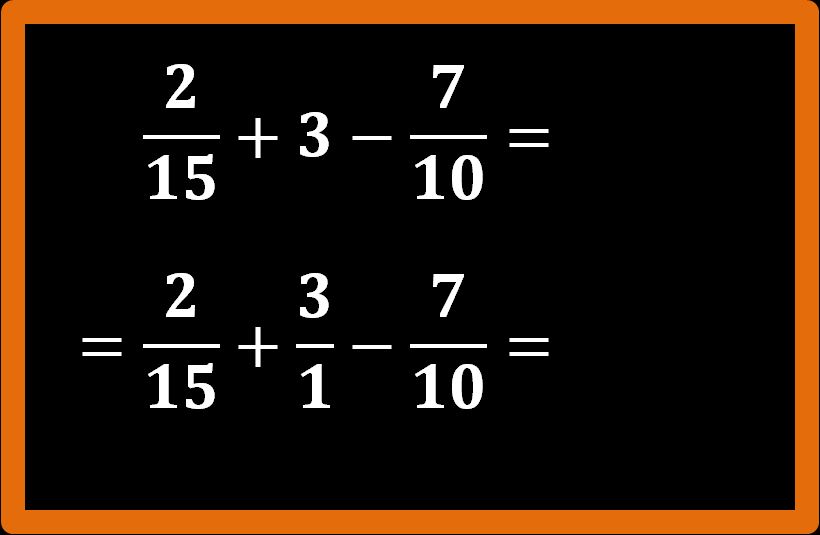
Ora, potrà anche essere che alla tua prof non piaccia questo modo di scrivere, ma non è scorretto. E poi penso che sia il modo migliore per imparare a eseguire operazioni del genere. In questo caso la mia opinione è che il fine giustifica i mezzi.
Procediamo normalmente ed eseguiamo l’addizione e la sottrazione tra frazioni che adesso sappiamo calcolare.
Per prima cosa scomponiamo in fattori primi i denominatori per calcolare l’m.c.m..
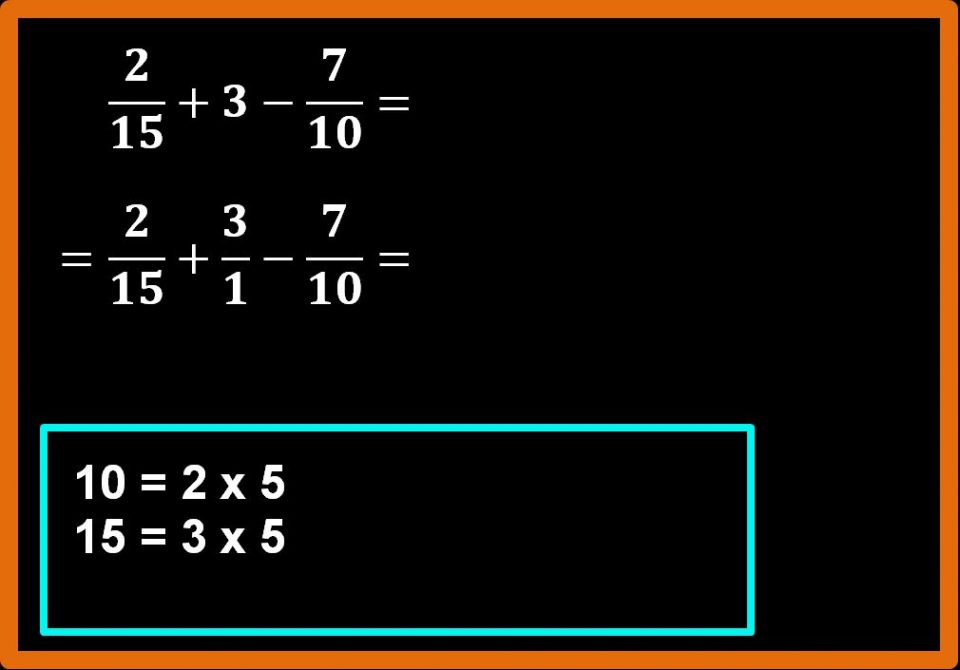
Scegliamo i fattori corretti e calcoliamo il minimo comune multiplo.

Adesso che abbiamo trovato l’m.c.m., tracciamo una bella linea di frazione e scriviamo al denominatore l’m.c.m. che abbiamo trovato.
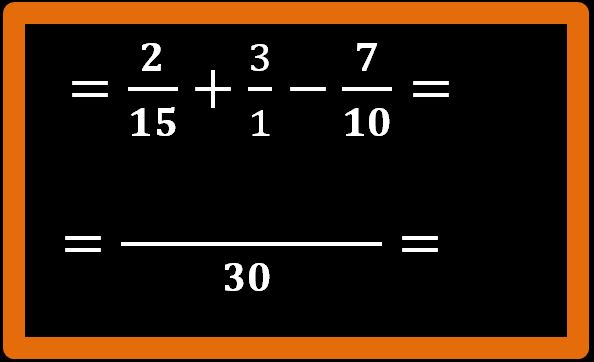
Procediamo come sappiamo:
30 : 15 = 2; 2 · 2 = 4;
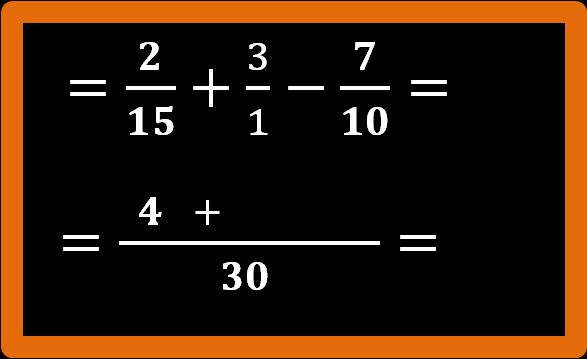
Stesso procedimento per la seconda frazione:
30 : 1 = 30; 30 · 3 = 90;
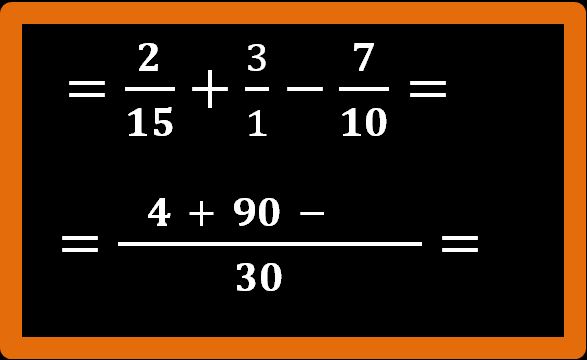
Ripetiamo il procedimento per l’ultima frazione.
30 : 10 =3; 3 · 7 = 21;
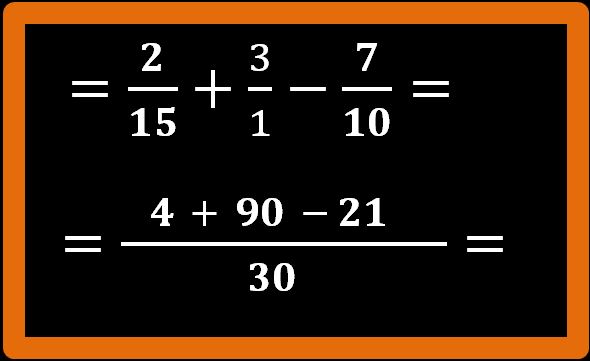
Eseguiamo adesso le operazioni che ci sono al numeratore:
4 + 90 – 21 = 73
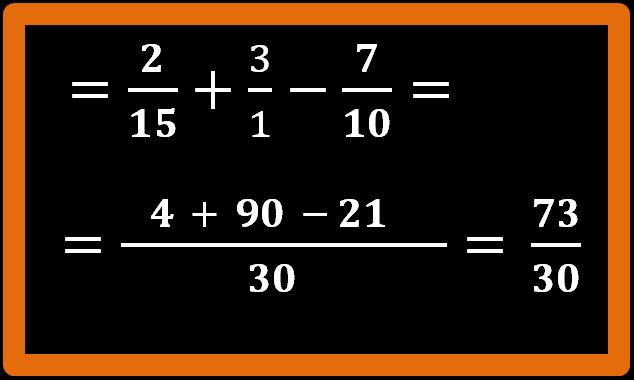
Perfetto, per essere sicuri di avere finito dobbiamo determinare se è possibile ridurre ai minimi termini il risultato che abbiamo ottenuto. Dobbiamo cercare di dividere per lo stesso numero sia il numeratore che il denominatore.
Però non sempre è possibile ridurre ai minimi termini, questo succede per esempio quando il numeratore o il denominatore sono numeri primi. Il 30 non è un numero primo, infatti è divisibile per 3, per 5 e per 10. Se vuoi ripassare i criteri di divisibiltà puoi leggere il mio articolo.
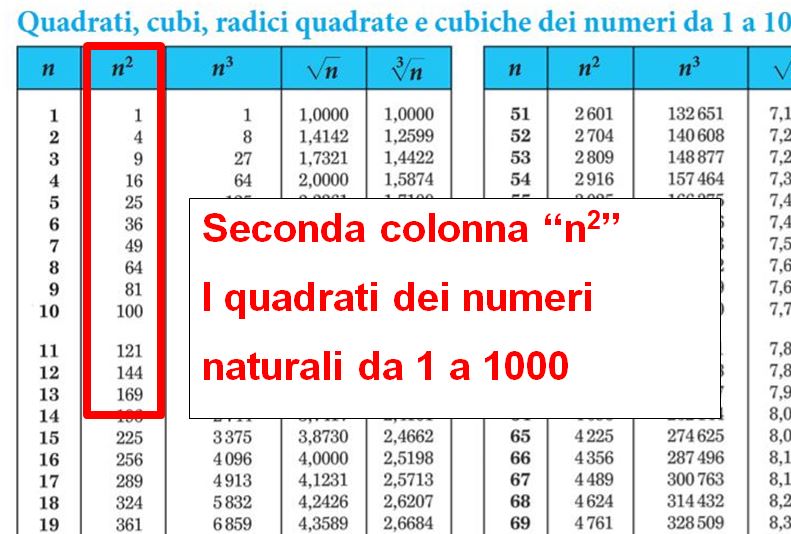
Il 73 potrebbe essere un numero primo. Solo le persone dotate di una memoria eccezionale possono ricordare i numeri primi fino al 100. Per tutte le altre persone (come me) esistono le tavole numeriche, che puoi portare in classe (a patto che non abbiano le formule) e puoi anche usarle durante le verifiche. Normalmente le tavole si trovano all’interno del primo volume del tuo libro di matematica. Ma se le hai perse o non ti ricordi più dove le hai posate non ti preoccupare. A questo link della Casa Editrice Zanichelli trovi le tavole in formato pdf. Le puoi consultare o scaricare.
Nelle tavole sono elencati i numeri primi fino al 10000. A pagina 11 troviamo quello che stavamo cercando.

Il numero 73 è un numero primo. Questo vuol dire che la frazione 73 fratto 30 è già ridotta ai minimi termini.
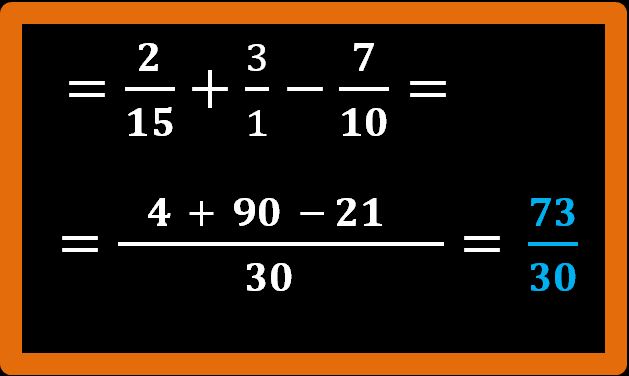
Quindi 73 su 30 è il risultato che stavamo cercando. Esercizio concluso.
esercizi in pdf
Se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf subito sotto. Puoi solo consultarlo oppure puoi anche stamparlo. Non ci sono tutti i risultati, ma solo quelli del primo e dell’ultimo esercizio. Per gli altri esercizi devi avere fiducia nelle tue capacità. Se il primo esercizio ti risulta, non c’è motivo per cui non ti risulti anche il secondo. E poi quando farai le verifiche in classe mica li avrai i risultati, quindi è meglio abituarsi.
![]() Addizioni e sottrazioni tra frazioni – Esercizi.pdf
Addizioni e sottrazioni tra frazioni – Esercizi.pdf
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.