Dopo avere fatto una introduzione alle proporzioni e avere visto la proprietà fondamentale delle proporzioni è arrivato il momento di usare questa proprietà per eseguire il calcolo del termine incognito di una proporzione.
Partiamo subito con un esempio numerico.
indice
esempio 1
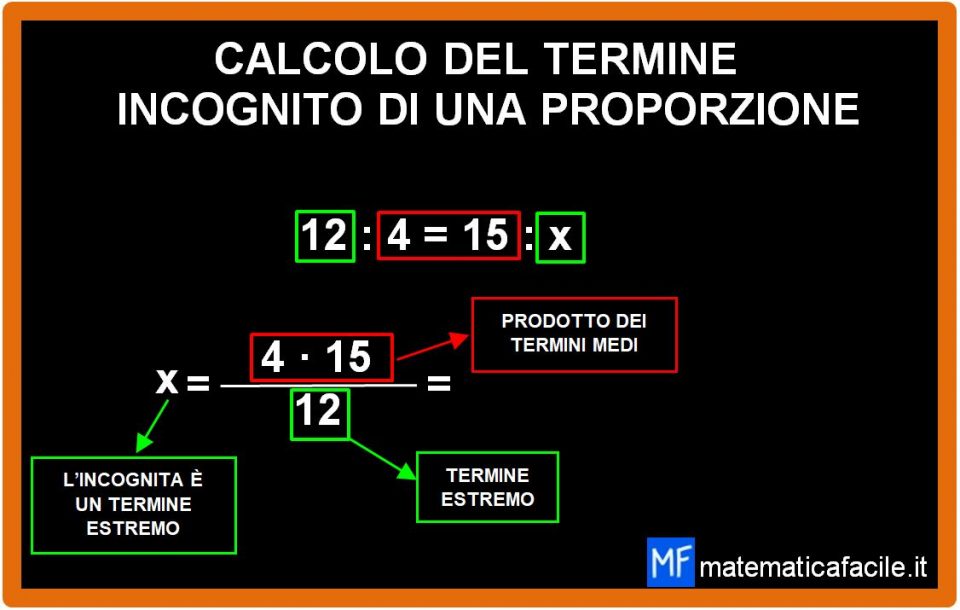
Consideriamo la proporzione scritta nella lavagna:
12 sta a 4 come 15 sta a x

Per calcolare il termine incognito dobbiamo:
- Capire se l’incognita è un termine medio o un termine estremo (se non ti ricordi quali sono i medi e gli estremi in una proporzione, potresti dare un’ occhiata al mio articolo introduzione alle proporzioni). Nel nostro caso la x è un estremo quindi dobbiamo
- moltiplicare tra loro i termini medi e
- dividerli per l’altro estremo.

Facciamo una cosa alla volta. Riscriviamo la x è tracciamo una linea di frazione.

Dato che la x è un estremo, al numeratore dobbiamo scrivere i termini medi moltiplicati tra loro.
Detto in altre parole, visto che la x è un estremo, al numeratore mettiamo il prodotto dei termini medi.

Bene, adesso al denominatore scriviamo l’altro termine estremo, cioè il 12.
Benissimo, adesso possiamo passare ai calcoli. Ci sono diversi modi per eseguire questi calcoli. Il modo che preferisco è semplificare il più possibile. Per esempio possiamo dividere per 3 sia il 15 al numeratore, sia il 12 al denominatore.

Fantastico, adesso possiamo dividere per 4 sia il 4 al numeratore, sia il 4 al denominatore.

Benissimo, al numeratore abbiamo la moltiplicazione
1 · 5 = 5
Invece al denominatore è rimasto solo il numero 1.

Benissimo. Abbiamo trovato il valore della x, cioè
x = 5
Andiamo quindi a scrivere al posto della x il numero 5.

Possiamo verificare se abbiamo lavorato bene applicando la proprietà fondamentale delle proporzioni, cioè il prodotto dei medi deve essere uguali al prodotto degli estremi.
Prodotto dei termini medi → 4 · 15 = 60
Prodotto dei termini estremi → 12 · 5 = 60
I due risultati sono uguali, per cui abbiamo lavorato bene. Il valore da dare alla x è 5. Abbiamo eseguito correttamente il calcolo del termine incognito di una proporzione.
Esercizio concluso.
esempio 2: la casa in affitto risolto senza usare le proporzioni
In un esempio presente in un altro articolo avevamo questa situazione: Linda e Andrea decidono di prendere in affitto una casa vicino al mare nel mese di giugno. L’ affitto per un mese costa 600 €, ma loro prendono in affitto la casa solo per 3 settimane, cioè 21 giorni. Quanto dovranno pagare?
La risposta a questa domanda si può trovare in diversi modi, per esempio si può seguire questo ragionamento: dividiamo il costo di un mese per 30 (i giorni totali del mese di giugno)
600€ : 30 giorni = 20 €/giorno (leggi 20 euro al giorno)
In questo modo abbiamo ottenuto il costo di un giorno di affitto. Adesso moltiplichiamo il costo di un giorno per 21, cioè i giorni in cui Linda e Andrea hanno deciso di prendere la casa in affitto.
20 €/giorno · 21 giorni = 420 €
Abbiamo ottenuto come risultato 420€, che è il risultato corretto.
esempio 2 usando le proporzioni
Cerchiamo adesso di usare le proporzioni e applichiamo la proprietà fondamentale per eseguire il calcolo del termine incognito di una proporzione.
La nostra domanda è:
Se 30 giorni costano 600 €, 21 giorni quanti euro costano?
Usando una proporzione:
30 : 600 = 21 : x
che ti ricordo si legge: 30 sta a 600 come 21 sta a x.
Benissimo. Dobbiamo calcolare la x. Abbiamo imparato che in una proporzione si possono individuare termini medi e termini estremi.
Nel nostro esempio la x, cioè la quantità che non conosciamo (l’incognita) è un termine estremo.
Per calcolare il valore della x dobbiamo :
- scrivere la x e tracciare una linea di frazione;
- al numeratore scrivere il prodotto dei termini medi, cioè 600 · 21;
- al denominatore scrivere l’altro termine estremo, cioè 30.

Abbiamo seguito lo stesso procedimento dell’esempio 1, ma i numeri sono diversi, infatti in questo caso abbiamo a che fare con numeri un po’ più grandi.
Anche in questo caso, si possono percorrere tante strade per effettuare i calcoli, ma credo che la via più conveniente sia semplificare fin quando è possibile.
Per esempio possiamo dividere per 10 sia il 600 al numeratore sia il 30 a denominatore, che detto in parole povere vuol dire eliminare uno zero dai due numeri.

Continuiamo a semplificare, possiamo infatti dividere per 3 sia il 21 al numeratore sia il 3 al denominatore.

Molto bene, non è più possibile semplificare, possiamo solo eseguire la moltiplicazione che compare al numeratore, 60 · 7. (Ricordiamoci che il numero 1 al denominatore non si scrive).

Bene, abbiamo ottenuto come risultato 420. Questa è la quantità di soldi che Linda e Andrea pagheranno per 3 settimane di affitto.
Possiamo riscrivere la proporzione di partenza sostituendo alla x il numero 420.

Esercizio concluso.
Esempio 3
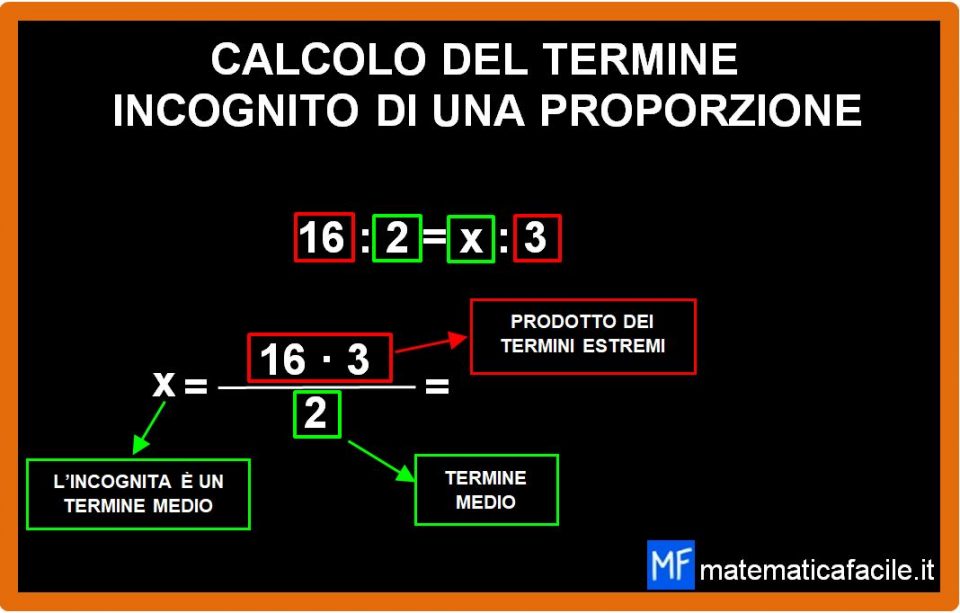
Facciamo ancora un esempio per essere sicuri di avere capito bene come si esegue il calcolo del termine incognito di una proporzione. Scriviamo la proporzione 16 sta a 2 come x sta 3.

Bene, i passaggi che dobbiamo seguire per determinare l’incognita sono sempre gli stessi:
- Capire se l’incognita è un termine medio o un termine estremo. Nel nostro caso la x è un medio quindi dobbiamo
- moltiplicare tra loro i termini estremi e
- dividerli per l’altro medio.
Passiamo ai calcoli. Semplifichiamo il 16 al numeratore e il 2 al denominatore dividendo tutto per 2.

Adesso eseguiamo il prodotto che compare al numeratore.

Abbiamo concluso. Abbiamo trovato il valore della x. Possiamo riscrivere la proporzione scrivendo al posto della x il numero 24.

Possiamo verificare se abbiamo lavorato bene applicando la proprietà fondamentale delle proporzioni, cioè il prodotto dei medi deve essere uguali al prodotto degli estremi.
Prodotto dei termini medi → 2 · 24 = 48
Prodotto dei termini estremi → 16 · 3 = 48
I due risultati sono uguali, per cui abbiamo lavorato bene. Il valore da dare alla x è 24. Abbiamo eseguito correttamente il calcolo del termine incognito di una proporzione.
Esercizio concluso.
esercizi in pdf
Adesso possiedi gli strumenti necessari per calcolare il termine incognito di una proporzione. Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Lavora con calma e non avere fretta di finire. Non ti preoccupare se sbagli. Sbagliare è normale. I risultati ti servono per capire se hai fatto bene.
![]() Calcolo del termine incognito di una proporzione – Esercizi.pdf
Calcolo del termine incognito di una proporzione – Esercizi.pdf
Buon lavoro
su youtube
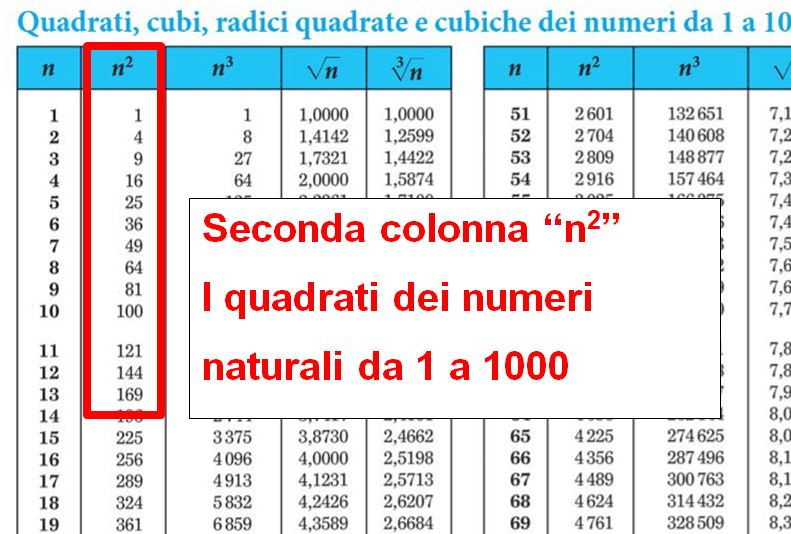
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare e/o scaricare le tavole numeriche.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.