Oggi la tua prof di matematica ha spiegato le unità di misura di superficie e lineari. Tu eri attento, ma non sei riuscito proprio a capire cosa sono i centimetri quadrati. Non preoccuparti, è una difficoltà comune. Con 5 minuti di impegno ti sarà tutto più chiaro. Ma basta con le parole, cominciamo con qualche esempio.
indice
area del rettangolo: formula diretta
Calcoliamo l’area del rettangolo in figura. Ti ricordo che l’area è la parte colorata di viola, cioè la zona interna della figura. Invece il contorno, quello arancione, è chiamato perimetro.
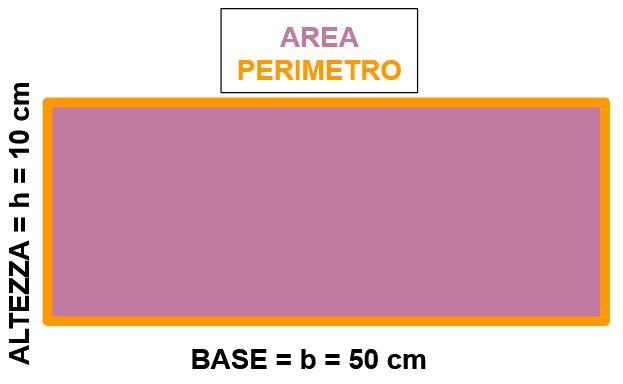
La formula che ci permette di calcolare l’area del rettangolo è :
Area del rettangolo → ARETT = base · altezza = b · h
Molto bene. Adesso passiamo ai numeri e vediamo cosa otteniamo.

Il risultato che abbiamo ottenuto è 500 cm2 (si legge cinquecento centimetri quadrati oppure 500 centimetri alla seconda).
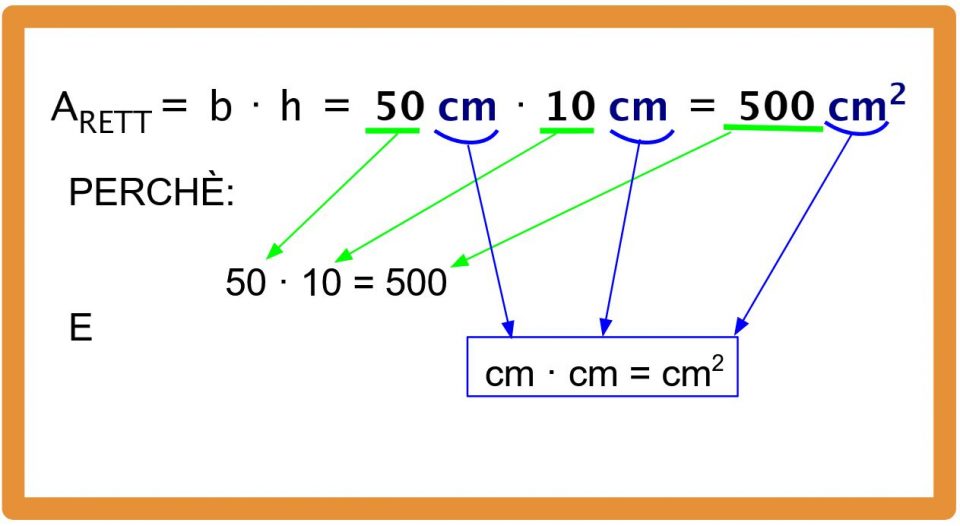
Bisogna fare un po’ di attenzione alle unità di misura.
Come abbiamo visto nell’esercizio appena svolto
cm · cm = cm2
Naturalmente il discorso vale anche per le altre unità di misura, per esempio:
m · m = m2
cioè metri per metri uguale metri quadrati,
oppure
km · km = km2
cioè chilometri per chilometri uguale chilometri quadrati.
formula inversa
Facciamo un altro esempio per cercare di capire le unità di misura di superficie e lineari. Guardiamo l’immagine in basso.
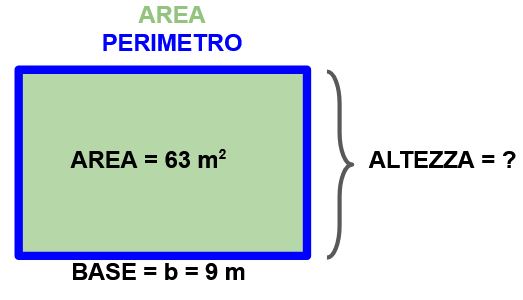
Del rettangolo in figura, conosciamo:
- l’area= A = 63 m2
- la base = b = 9 m
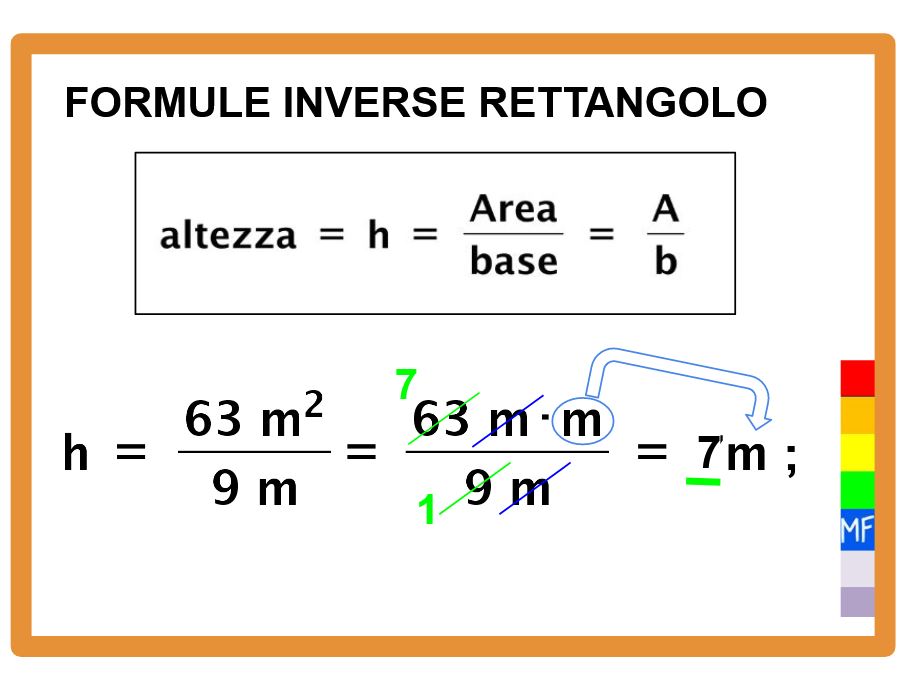
Vogliamo conoscere l’altezza. La formula per determinare l’altezza conoscendo l’area e la base la puoi leggere nella lavagna sotto.

Passiamo ai numeri:
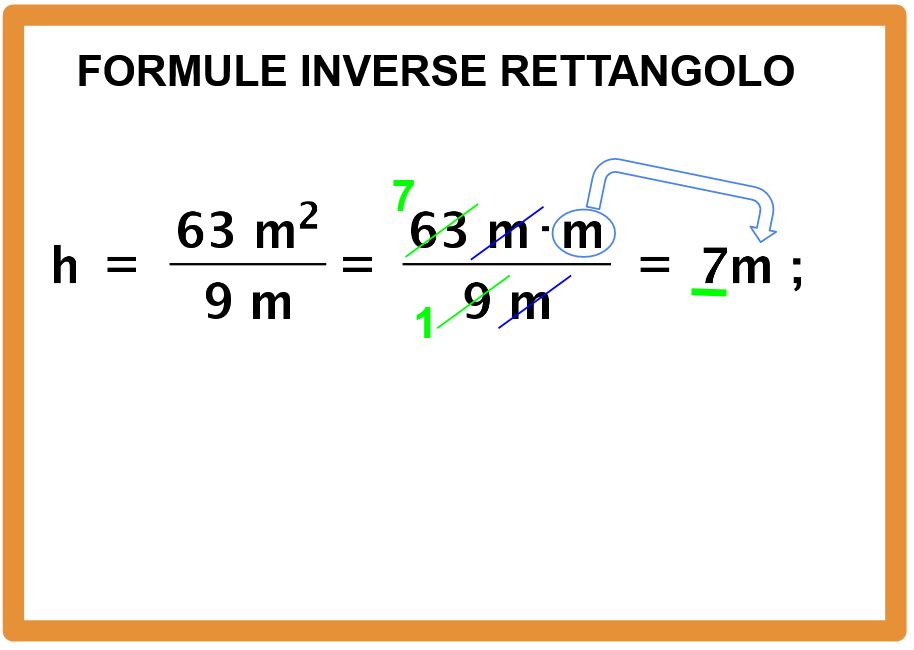
Il risultato che stavamo cercando è 7 m.
Riassumendo:
esercizi in pdf
Se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf in basso. Lavora con calma e non ti preoccupare se sbagli. Nessuno verrà a rimproverarti.
![]() Formule dirette e inverse – Esercizi.pdf
Formule dirette e inverse – Esercizi.pdf
Buon lavoro.
Cliccando qui si aprirà una nuova pagina in cui potra scaricare gratuitamente le tavole numeriche.
Se hai delle domande o vuoi segnalare un errore puoi scrivere alla casella mail matematica.facile@libero.it; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.