Se sei finito su questa pagina vuol dire che il primo criterio di congruenza dei triangoli ti sta dando qualche problema. Non ti preoccupare è una cosa comune, ma niente paura con 5 minuti di impegno capirai quando si usa e come si applica.
indice
- A cosa servono i criteri di congruenza
- Primo criterio di congruenza
- Primo esempio
- Secondo esempio
- Terzo esempio
- Esercizi
- Soluzioni
A cosa servono i criteri di congruenzA
I criteri di congruenza servono per capire se due triangoli sono uguali oppure no ( e servono anche per ottenere un buon voto nella verifica 😊).
La tua prof probabilmente avrà detto:
“Servono per determinare se due triangoli sono congruenti“.
Se ti stai chiedendo qual è la differenza tra uguale e congruente potresti leggere il mio articolo: differenza tra uguale e congruente.
In questo articolo vedremo cosa dice e come si applica il primo criterio di congruenza.
primo criterio di congruenza
Prima di vedere cosa dice il primo criterio, diamo un’occhiata ai due triangoli in basso e cerchiamo di determinare se sono uguali oppure sono diversi. Ricordati che la loro posizione non ha nessuna importanza quando dobbiamo determinare se sono uguali oppure no. Pensa a due gemelli identici. Anche se uno di loro è in piedi e l’altro è seduto, sono sempre due gemelli identici indipendentemente dalla loro posizione. Vale la stessa cosa per i triangoli.
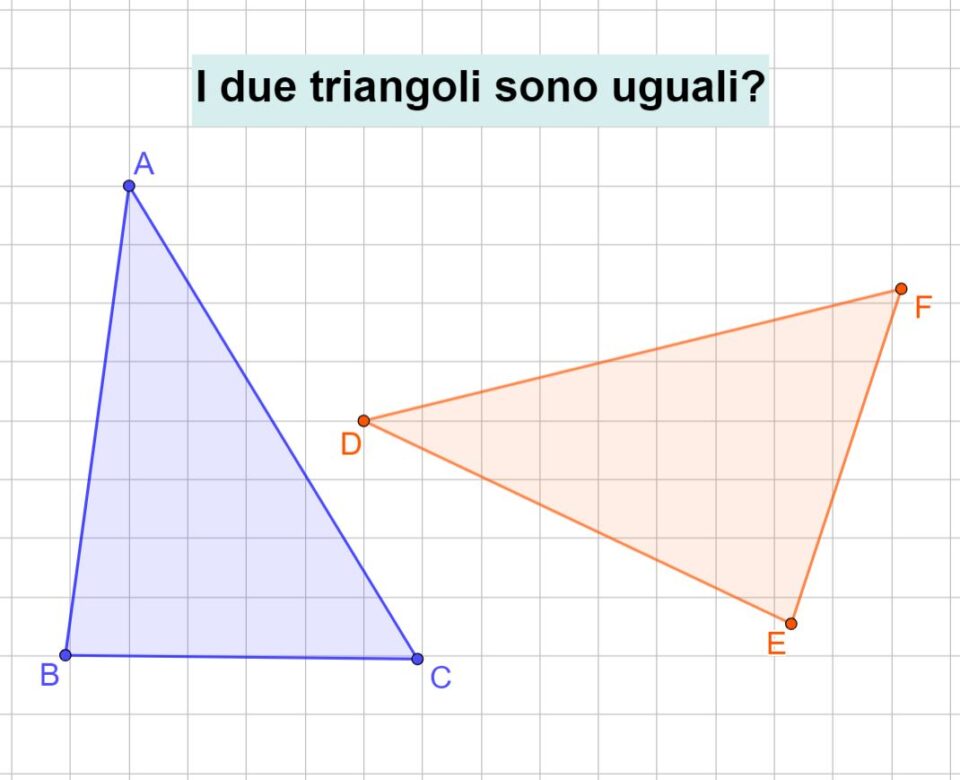
Non dobbiamo avere fretta di rispondere. Prima di dire sì oppure no, bisogna ricordare cosa si intende per uguali in geometria:
“due triangoli (ma vale anche per gli altri poligoni) sono uguali ( si potrebbe anche dire sono congruenti) se sono sovrapponibili, cioè se mettendoli l’uno sull’altro tutti i lati e tutti gli angoli corrispondono”.
Primo esempio
Torniamo ai due triangoli del nostro esempio. Per essere congruenti devo poterli sovrapporre e uno deve essere la copia esatta dell’altro. Il breve video in basso illustra quello che hai apena letto. Se non l’hai ancora fatto, potresti iscriverti al nostro canale YouTube cliccando su “Iscriviti”.
Anche se a prima vista sembrano diversi, i due triangoli grazie a una rotazione e una traslazione possono essere sovrapposti e i loro vertici corrispondono perfettamente, questo vuol dire che i due triangoli sono congrunti.
Però capisci bene che se lavoriamo con il quaderno, l’unico modo per ruotare e traslare le figure sarebbe ritagliare la pagina e di sicuro la tua prof non sarebbe contenta.
Dobbiamo trovare un metodo che ci permetta di determinare se due triangoli sono uguali senza usare GeoGebra e senza ritagliare la pagina del tuo quaderno 😉🤔.
Questo metodo è il primo criterio di congruenza. Però per applicarlo dobbiamo conoscere la lunghezza di due lati del triangolo e l’ampiezza dell’angolo che questi due lati formano. È poco chiaro? Non ti preoccupare. Aiutiamoci con l’immagine in basso.

I due triangoli hanno i lati AB e DE uguali, infatti hanno la stessa lunghezza, cioè 8.

Se guardiamo con attenzione, anche il lato BC del triangolo blu e il lato EF del triangolo rosa sono uguali e misurano 6.

Ma non solo, l’angolo in B del triangolo blu e l’angolo in E del triangolo rosa sono uguali.
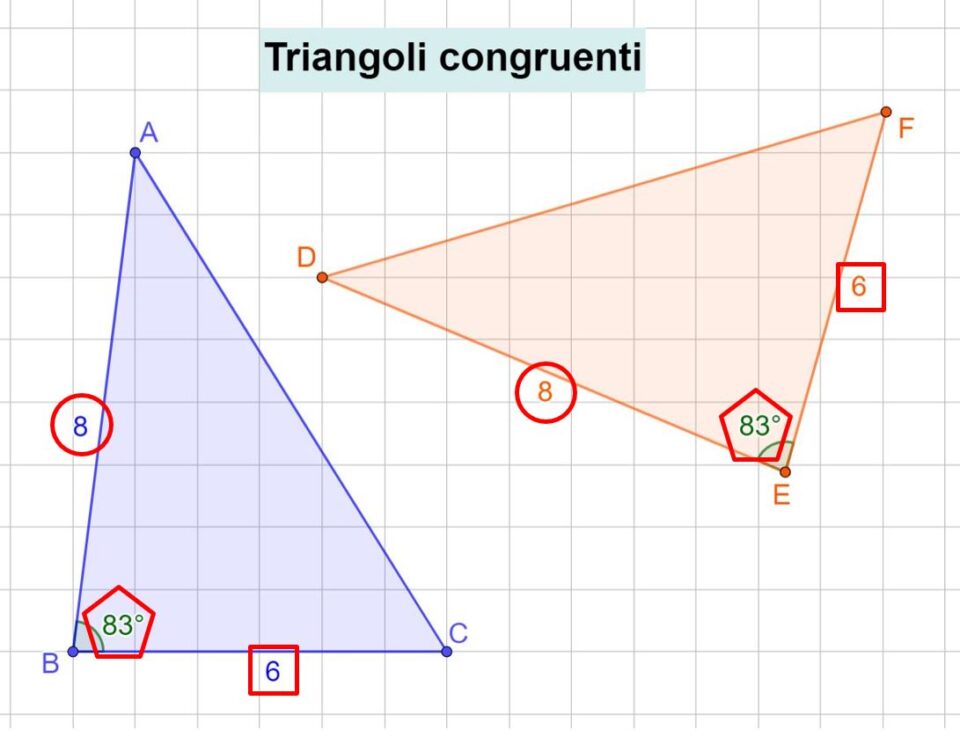
In conclusione, i due triangoli hanno due lati uguali e l’angolo che questi due lati formano uguale. Allora possiamo affermare che i due triangoli sono uguali per il primo criterio.
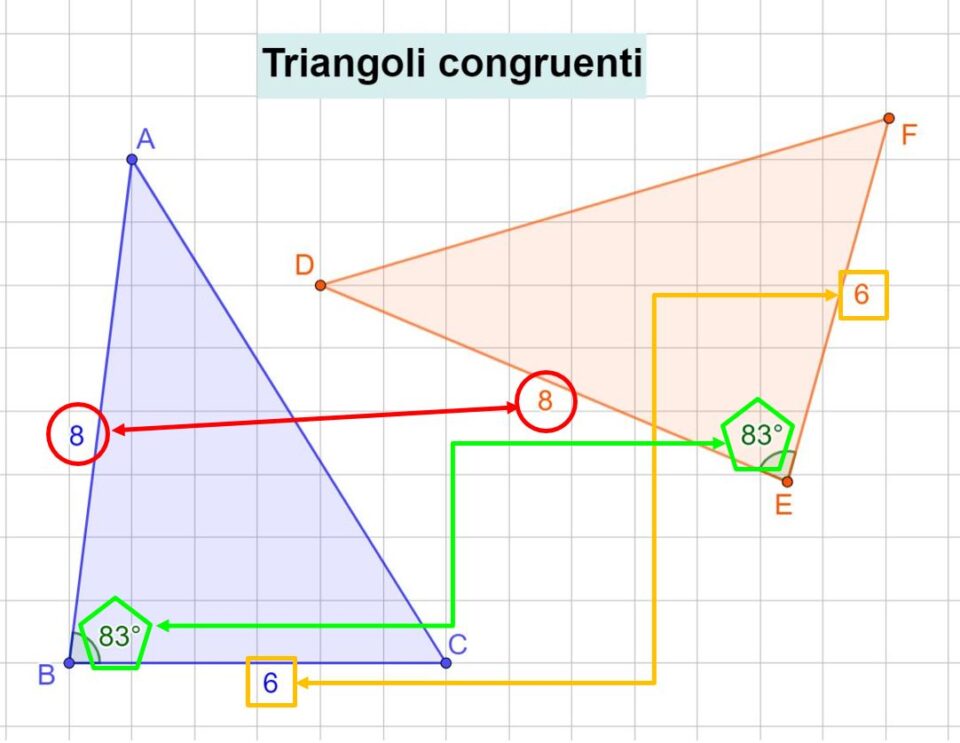
Secondo esempio
Vediamo un altro esempio di applicazione del primo criterio di congruenza dei triangoli. Cerchiamo di determinare se i due triangoli nella figura sono congruenti oppure no.
Ricorda, dobbiamo osservare la lunghezza dei lati e l’ampiezza degli angoli.
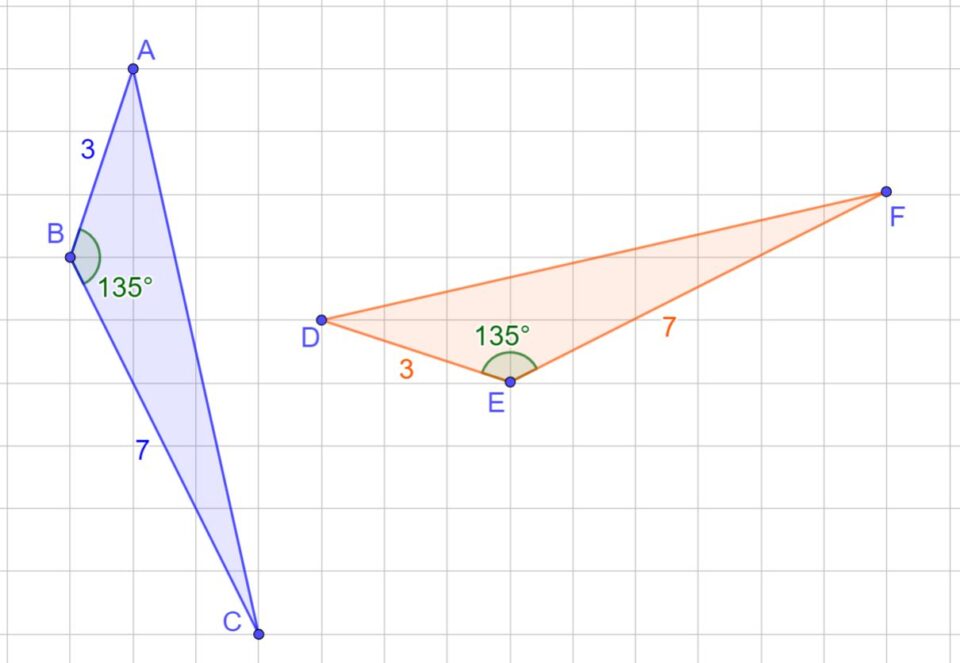
I due triangoli della figura hanno due lati uguali, infatti
AB = DE
e anche
BC = EF
ma abbiamo anche l’angolo che questi lati formano è uguale, infatti
l’angoli in B è uguale all’angolo in E → 135°.
I due triangoli, hanno due lati uguali e l’angolo tra essi compreso uguale.
Terzo esempio
Cerchiamo di determinare se i due triangoli in figura sono congruenti oppure no. Bisogna vedere se è possibile applicare il primo criterio di cpngriuenza, cioè due lati dei triangoli devono essere uguali e deve essere uguale anche l’angolo che essi formano.
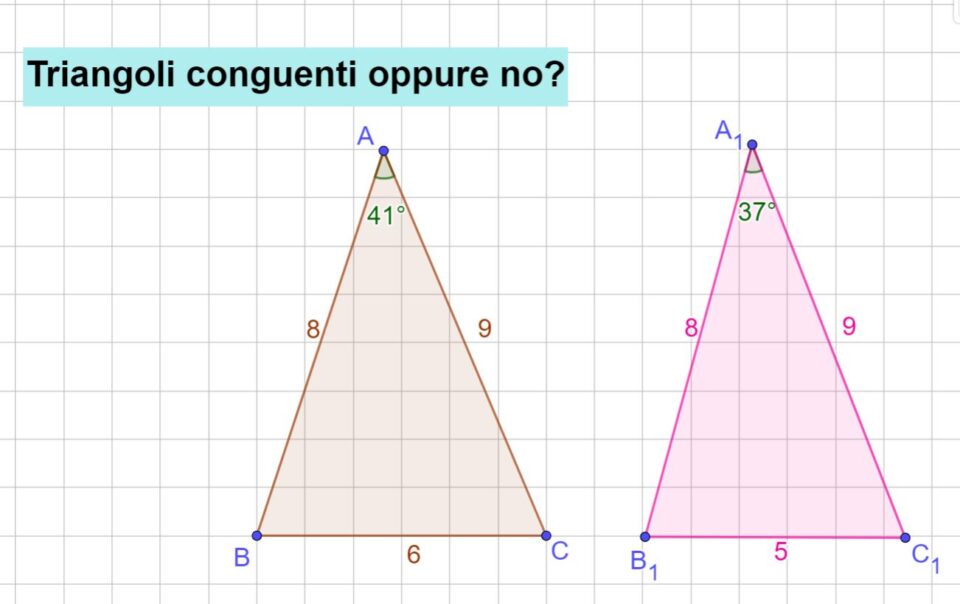
Il breve video in basso illustra il procedimento seguito e il risultato.
iscriviti al nostro canale YouTube
Esercizio 1
Guarda con attenzione le immagini che seguono e dopo aver ripassatoil primo criterio di congruenza, rispondi alla domanda.

Quale elemento dei due triangoli è necessario conoscere per poter applicare il primo criterio? Solo una risposta è quella corretta.
- Il lato AC e il lato FD;
- L’ angolo in B e l’angolo in E;
- L’ angolo in F e l’ angolo in C.
Esercizio 2
Guarda con attenzione le immagini che seguono e dopo aver ripassatoil primo criterio di congruenza, rispondi alla domanda.

Quale elemento dei due triangoli è necessario conoscere per poter applicare il primo criterio?
esercizio 3
Osserva i due triangoli e stabilisci se sono congruenti oppure no. Motiva la tua risposta.

Soluzioni
- Esercizio 1 → è necessario conoscere l’ampiezza degli angoli in B e in E.
- Esercizio 2 → è necessario conoscere la lunghezza dei lati AC e FD che assieme ai lati BC e EF formano gli angoli retti.
- Esercizio 3 → i due triangoli non sono congruenti. Infatti anche se hanno un lato uguale e un angolo uguale, l’altro lato che forma l’angolo (di cui conosciamo l’ampiezza) nei due triangoli ha lunghezza diversa, nel prim 7,5 e nel secondo 8,3.