In questo articolo vedremo come si calcola l’area del cerchio. Useremo anche le formule inverse, quindi riusciremo a determinare la lunghezza del raggio conoscendo l’area. Ma basta con le parole, facciamo subito un esempio.
Indice
Primo esempio
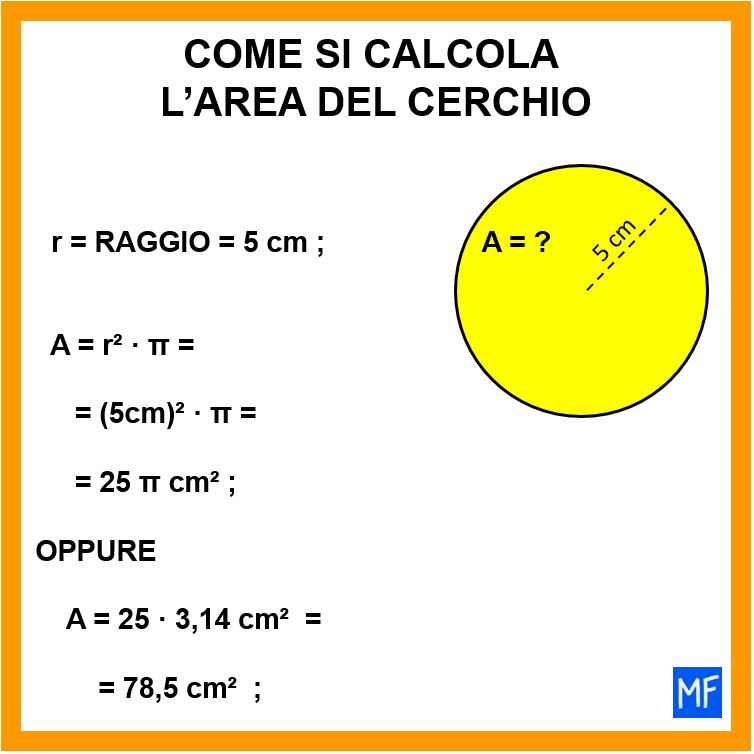
Calcoliamo l’area del cerchio che vedi alla lavagna. Il raggio è lungo 5 cm.

La formula che ci permette di calcolare l’area del cerchio è
A = π · r² → (si legge pi greco per erre alla seconda)
che scritta in un altro modo diventa
A = π · r · r → (si legge pi greco per erre per erre)
Al posto di r sciviamo 5 cm e otteniamo
A = π · 5 cm · 5 cm
Eseguiamo le moltiplicazioni lasciando il π indicato.
A = 25 π cm²
Questo è il risultato che stavamo cercando.
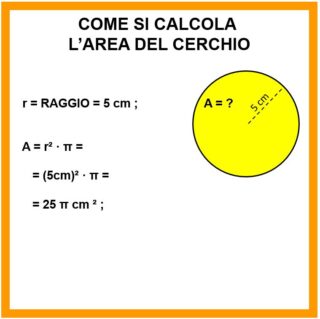
Se diamo al π il valore di 3,14 otteniamo come risultato
A = 78,5 cm²
Bisogna tenere presente che A = 25 π cm² e A = 78,5 cm² sono entrambi risultati corretti. Devi solo fare attenzione a rispettare la consegna. Se ti chiede di lasciare indicato il pi greco allora va lasciato indicato. Se invece ti chiede di dare al pi greco il valore di 3,14 devi fare i calcoli usando quel valore.
Esercizio concluso.
Secondo esempio
Facciamo un altro esempio per cercare di capire come si calcola l’area del cerchio. Guardiamo la figura alla lavagna e con i dati che abbiamo a disposizione cerchiamo di calcolare l’area del cerchio.
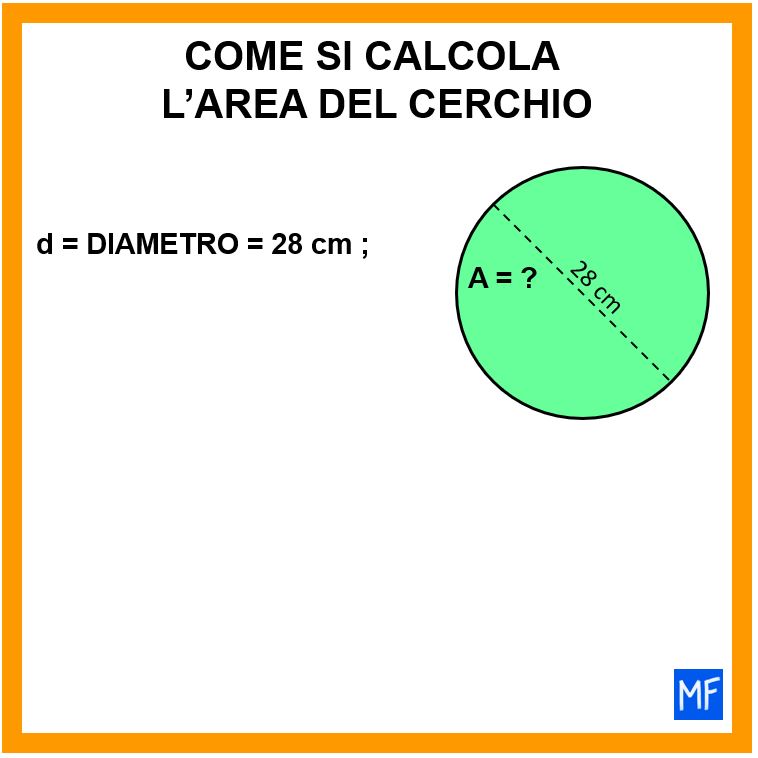
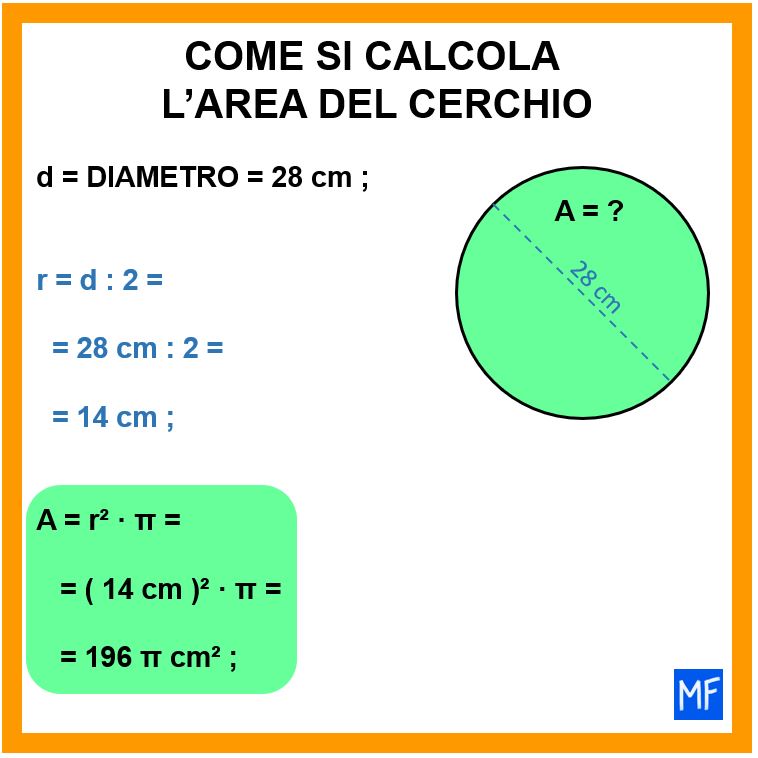
Sappiamo che il diametro misura 28 cm. Per potere calcolare l’area ci serve la misura del raggio e non quella del diametro. Ma possiamo ottenere il raggio dividendo il diametro per 2, infatti il raggio è la metà del diametro.
raggio = diametro : 2
Usando i simboli si ha che
r = d : 2
Al posto della “d” inseriamo il valore 28 cm
r = 28 cm : 2 = 14 cm
Adesso che abbiamo ottenuto la misura del raggio, possiamo calcolarci l’area del cerchio. La formula è sempre la stessa:
A = r² · π
Sostituiamo mettendo “14 cm” al posto di “r”
A = (14 cm)² · π =
Aiutandoci con le tavole numeriche oppure con la calcolatrice, otteniamo che
A = 196 π cm² (si legge 196 pi greco centimetri alla seconda oppure centrimetri quadrati)
oppure
A = 615,44 cm²
Terzo esempio
Facciamo ancora un esempio che riguarda l’area del cerchio. Guardando la figura in basso sappiamo quanto misura l’area del cerchio. Dobbiamo ricavare il raggio.
A = 169 π cm²
Ci dobbiamo servire della formula inversa che leggi alla lavagna. Le formule inverse possono essere ricordate oppure possono essere ricavate dalle formule dirette.
La formula inversa che ci serve è raggio = radice quadrata di area fratto pi greco → è scritta nella lavagna in basso.
Il π al numeratore e il π al denominatore si possono semplificare poichè sono la stessa quantità.
La radice quadrata di 169 è 13 e quindi…
Il risultato che stavamo cercando è r = 13 cm .

Quarto esempio
Facciamo ancora un esempio per cercare di capire meglio come si calcola l’area del cerchio. Osservando la lavagna in basso, vedi che conosciamo la lunghezza della circonferenza (CRF alcuni libri per indicare la cirnconferenza usano la lettera maiuscola C, io preferisco usare CRF. Tu usa il simbolo che utilizza la tua prof.)

Per calcolare l’area, ci serva sapere la lunghezza del raggio. Quindi dobbiamo usare la formula inversa che dalla cirocnferenza ci permette di calcolare il raggio. Guardiamo la lavagna sotto.
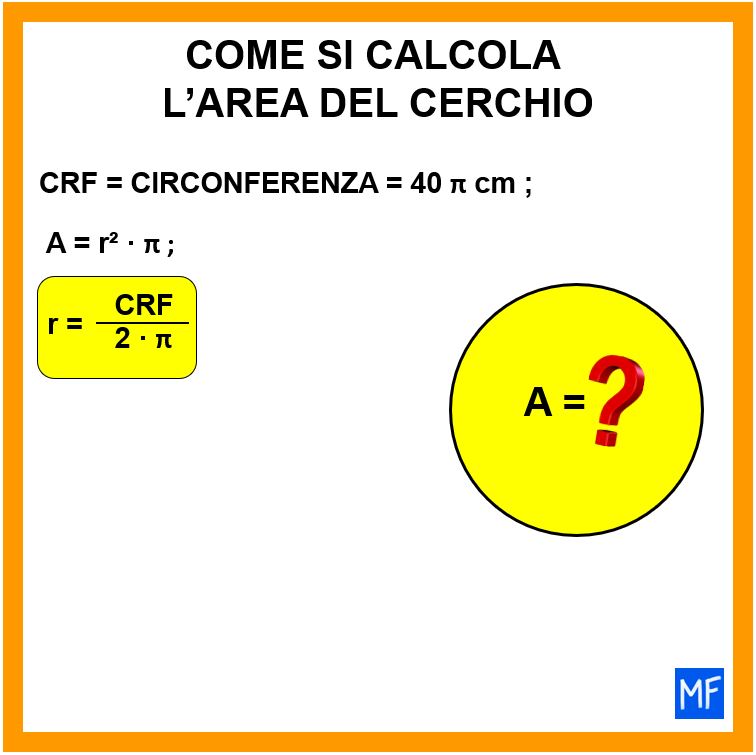
Ora che abbiamo individuato la formula da usare, non ci rimane che sostituire al posto di CRF il valore della lunghezza della circonferenza ed eseguire i calcoli.

Abbiamo finalmente ottenuto la lunghezza del raggio che è 20 centimentri. Adesso possiamo usare questo dato per calcolare l’area, con la formula che abbiamo visto negli esempi precedenti.

Esercizio concluso. L’area del cerchio misura 400 π cm² (si legge 400 pi greco centimetri quadrati).