Mentre scrivo questo articolo il termometro della farmacia che vedo dalla mia finestra segna la temperatura di -3° C (si legge meno tre gradi Celsius). Il numero che hai appena letto ha il segno meno davanti. I numeri che sono preceduti da un segno ( che può essere più “+” oppure meno “–“) in matematica sono chiamati numeri relativi (qualche libro li chiama anche numeri interi, io ti consiglio di utilizzare il nome usato dalla tua prof). In questo articolo cercheremo di capire cosa sono e come si confrontano i numeri relativi.
In inglese sono chiamati signed numbers, cioè numeri segnati. Il nome è appropriato perchè i numeri relativi sono quei numeri che davanti hanno il segno + oppure il segno – .
iscriviti al nostro canale Youtube
indice
qualche notizia sui numeri relativi
I numeri relativi possono essere positivi (se hanno davanti il segno più, ad esempio +25) oppure negativi (se hanno davanti il segno meno, ad esempio -3). A noi sembrano numeri normali, la loro esistenza ci sembra banale, anzi senza numeri negativi come faremmo a indicare le temperature quando fa molto freddo? Ma non è sempre stato così. Nei secoli passati i numeri negativi venivano considerati “numeri surdi”, cioè numeri assurdi. Infatti per molti matematici del passato i numeri negativi non avevano proprio senso. Dobbiamo ricordarci che il termometro è un invenzione recente (inventato da Galileo nel 1600 circa).
Uno dei pochi matematici ad accorgersi dell’utilità dei numeri relativi fu Raffaele Bombelli, nato a Bologna qualche anno dopo l’approdo di Colombo in America.

Bombelli dice:
“Se sono in debito con un mio amico di 25 € (ai suoi tempi c’erano gli scudi), ma ho in tasca solo 20 €, vuol dire che devo ancora restituire 5 €”.
Usando i numeri potremmo scrivere:
20€ – 25€ = -5€
Quindi i numeri relativi possono essere usati per tenere la contabilità, oppure per sapere che temperatura c’è fuori. Ma ti ripeto, in passato, anche grandi matematici (G. Cardano, A. Arnauld) ritenevano i numeri relativi quasi impossibili o inaccettabili.
Di contro, molti matematici arabi già nel 1100 operavano con i numeri negativi. Questo non deve sorprendere. Con molta probabilità, il capitolo del tuo libro di matematica che parla dei numeri relativi è il terzo volume (quello che si usa in terza media) e sul terzo volume quasi sicuramente c’è scritto Algebra. La parola ‘algebra‘ è di origine araba, deriva da al-giabr. Ricordiamoci che sono stati gli arabi che hanno portato i numeri che noi usiamo in Europa dall’India, per questo motivo sono chiamati numeri indo-arabi.
primo esempio
Dopo questa premessa di storia della matematica, vediamo come si confrontano i numeri relativi. Ti ricordo che in matematica confrontare vuol dire stabilire quale numero è maggiore. In un altro articolo avevamo visto per esempio come confrontare le frazioni. In altre parole vogliamo capire quale numero è più grande tra -3 e -8.
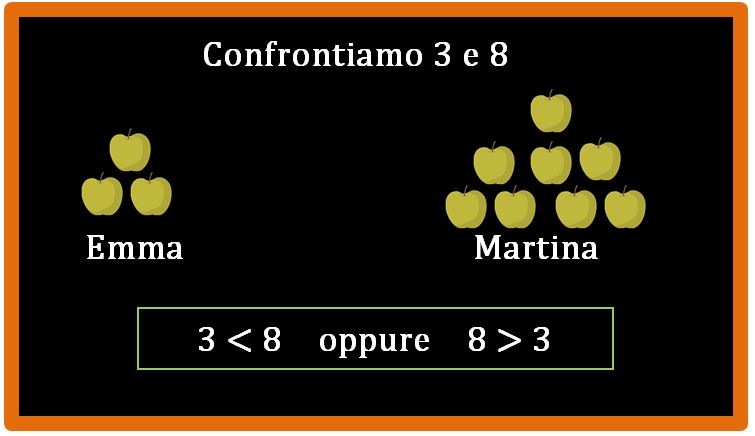
Se ti chiedessi quale numero è più grande tra 3 e 8, sono sicuro che non avresti dubbi sulla risposta. È più grande il numero 8. Alle elementari forse ti hanno fatto questo esempio: “Se Emma ha 3 mele e Martina ha 8 mele. Chi ha più mele?” La risposta è Martina, perchè 8 è maggiore di 3.
Ma se ti chiedo:
“Qual è il numero più grande tra -3 e -8?”
La risposta non è per niente banale. Non possiamo fare lo stesso ragionamento con le mele, perchè non ha senso dire: “Emma ha -3 mele”. Per rispondere in modo corretto possiamo aiutarci con la retta numerica.

È arrivato il momento di chiarire un concetto. Quando si ha a che fare solo con i numeri positivi, spesso il segno “+” non viene scritto. Usando i numeri si può dire che:

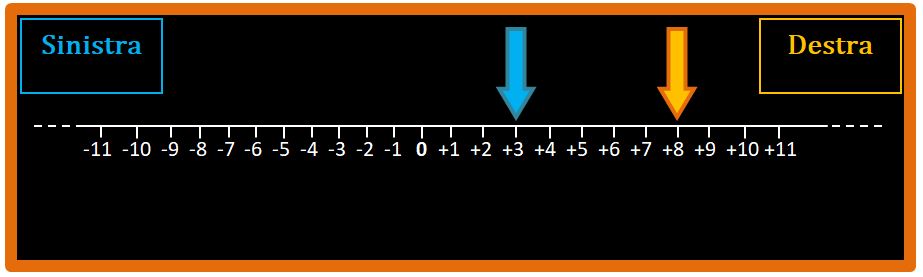
Molto bene. Chiarito questo, torniamo alla retta numerica e alle mele. Se voglio trovare sulla retta il numero 3 (le mele possedute da Emma) devo cercare il numero +3. Allo stesso modo, se voglio trovare il numero 8 (le mele possedute da Martina) devo cercare il numero +8. Andiamo a cercare i numeri che ci interessano e tracciamo due frecce per evidenziarli.

La regola generale, che vale sempre per tutti i numeri è questa:
“Il numero maggiore è quello che si trova più a destra“.
Possibilmente qualcuno potrebbe confondere la destra con la sinistra. Per evitare questa confusione è possibile ricordare che tutti noi scriviamo da sinistra → verso destra →. In questo momemto stai leggendo le parole spostando il tuo sguardo da sinistra e verso destra.
(Invece Leonardo da Vinci scriveva da destra ← a sinistra ←, cioè esattamente al contrario di come facciamo noi).
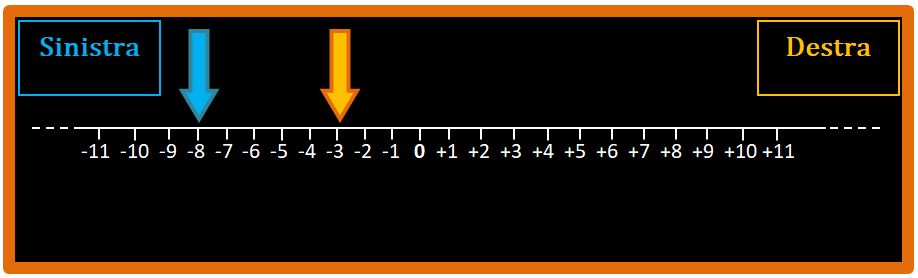
Benissimo, adesso siamo in grado di dire quale numero è più grande tra -3 e -8. Per prima cosa andiamo a individuarli sulla retta numerica.
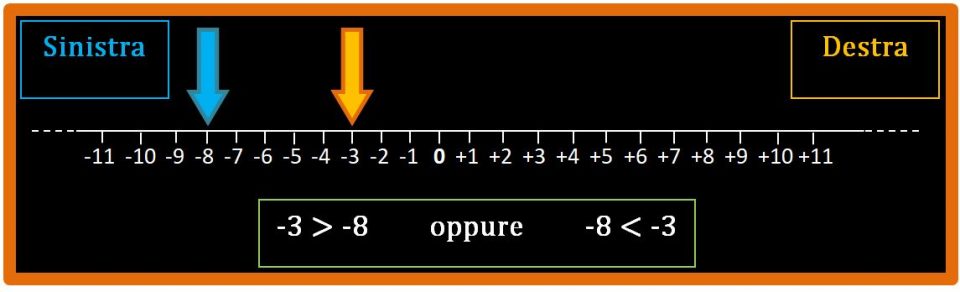
Fantastico. Ora, aiutandoci anche con le frecce di colore diverso dobbiamo stabilire quale dei due numeri si trova più a destra. Se guardiamo la retta ci rendiamo conto che il numero che si trova più a destra è il -3. Possiamo quindi affermare con sicurezza che -3 è più grande di -8.
secondo esempio
Facciamo un altro esempio per essere sicuri di avere capito bene cosa sono e come si confrontano i numeri relativi. Confrontiamo i numeri -7 e -1. Ci aiutiamo sempre con la retta numerica. Per prima cosa andiamo a individuare i due numeri.
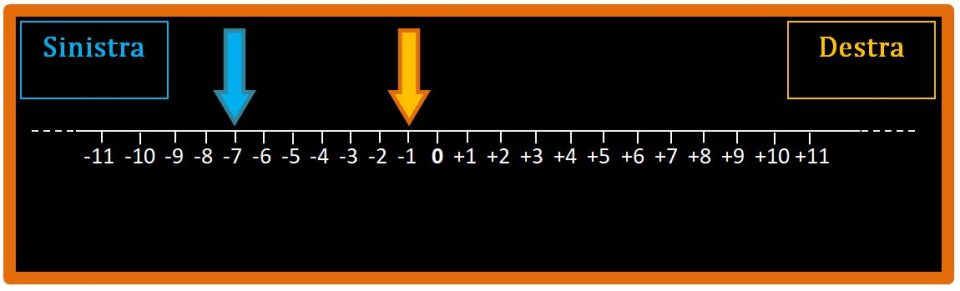
Fantastico. Il numero che si trova più a destra tra i due, sarà il numero maggiore.

Si legge così:
-1 è maggiore di -7 oppure -7 è minore di -1
Esercizio concluso.
esercizi
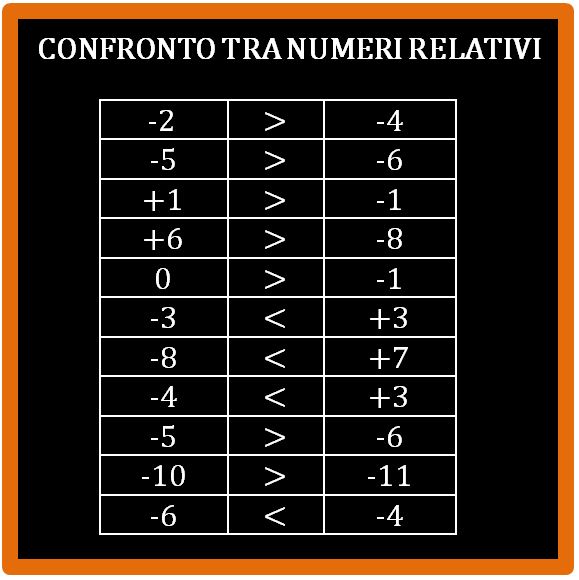
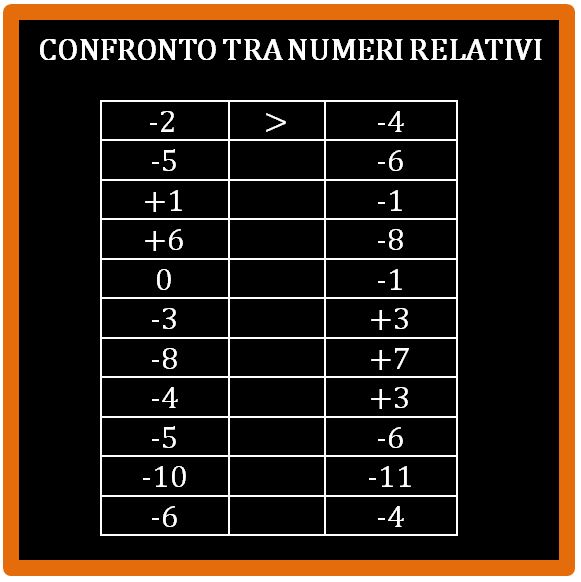
Adesso se vuoi puoi metterti alla prova, per vedere se hai capito cosa sono e come si confrontano i numeri relativi. Meglio se prendi carta e penna. Nella tabella che vedi sotto devi inserire il simbolo corretto, sceglieno tra < e >. Usa la retta dei numeri, lavora senza premura e non ti preoccupare se sbagli. Nessuno verrà a rimproverarti e poi sbagliando si impara. La prima riga è già svolta, completa le altre. Trovi i risultati alla fine della pagina.
Esercizi in pdf
Se vuoi, puoi anche allenarti con gli esercizi che trovi nel file pdf sotto. E ti ripeto: lavora senza fretta e anche se sbagli, non ti preoccupare. Sbagliando si impara.
![]() Confronto tra numeri relativi – Esercizi.pdf
Confronto tra numeri relativi – Esercizi.pdf
Buon lavoro.
Se hai domande o vuoi segnalare un errore puoi scrivere alla nostra casella mail: matematica.facile@libero.it ; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’ articolo.
Risultati