Oggi la prof ha spiegato la proporzionalità inversa, ma tu eri distratto e non sei riuscito a capire tanto bene. Niente paura con 5 minuti di impegno saprai cosa si intende per grandezze inversamente proporzionali.
Esempio 1
La migliore cosa da fare per capire le grandezze inversamente proporzionali è partire con un esempio numerico.
Giulia e Sofia sono due alunne della 2ª B e decidono di fare un regalo alla loro prof di matematica che il prossimo anno andrà in pensione. Nella loro classe sono in 24. Il regalo che decidono di comprare alla prof costa 96 €. Vediamo quanti soldi deve mettere ognuno di loro.
Se le uniche due persone che vogliono fare il regalo alla prof sono Sofia e Giulia, ognuna di loro deve versare 48€, dato che il regalo che hanno scelto costa 96€
96 € : 2 = 48 €
Cominciamo a realizzare una tabella che ci aiuterà a tenere a mente i numeri.
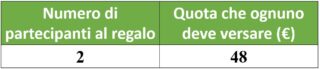
Supponiamo adesso che Sofia e Giulia riescano a convincere anche Martina.
La quota sarà:
96 € : 3 = 32 €
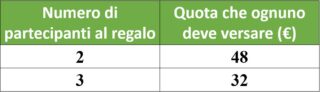
Martina a sua volta ne parla con Aurora e anche lei è d’accordo. Quindi saranno in 4 a partecipare al regalo.
Dato che sono in 4 la quota che ognuna di loro dovrà versare diminuisce.
96 € : 4 = 24 €
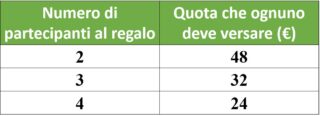
La voce del regalo si sparge e altri 8 compagni decidono di partecipare. Adesso in totalei partecipanti sono 12. Il costo del regalo è sempre lo stesso, ma la quota che ognuno di loro deve versare si abbassa.
96 € : 12 = 8€
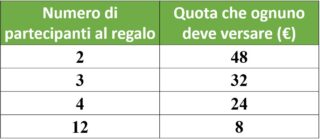
Anche gli altri compagni non vogliono essere esclusi dal regalo e alla fine tutta lclasse decide di partecipare, quindi la quota procapite ( procapite significa “a testa”; sinonimo → cadauno ) sarà di
96 € : 24 = 4€
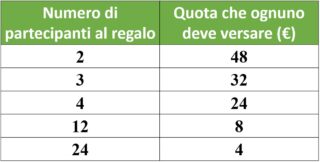
Come avrai intuito, più sono i partecipanti al regalo, più piccola è la quantità di soldi che ognuno di loro dovrà mettere. Detto in altre parole:
se il numero di partecipanti aumenta, la quota che ognuno deve versare diminuisce.
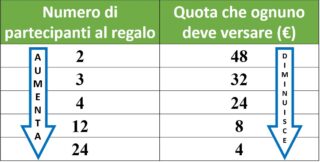
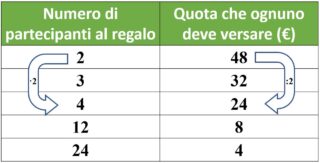
Non solo, se il numero di partecipanti raddopia, la quota per ognuno di loro diventa la metà.
Se moltiplichiamo per 6 la prima quantità, la seconda sarà divisa per 6.
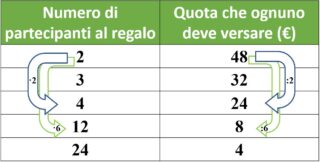
Questo tipo di quantità (una raddopia e l’altra dimezza) sono dette grandezze inversamente proporzionali.
Grafico
Realizziamo il grafico di queste due grandezze: numero di partecipanti e quota di partecipazione e vediamo cosa otteniamo.
Puoi vedere la realizzazione del grafico cliccando sul video del nostro canale YouTube che vedi in basso.
