Oggi la tua prof ha spiegato un argomento che proprio non hai capito. Hai sentito parlare di quadrilateri inscrivibili e di circonferenza, ma non sei riuscito a seguire bene. Non ti preoccupare, con 5 minuti di impegno saprai determinare quando un quadrilatero è inscrivibile in una circonferenza.
Indice
- Cose da sapere
- Piccolo esercizio
- Criterio per determinare se un quadrilatero è inscrivibile
- Il rettangolo
- Il quadrato
- Il parallelogramma
- Il rombo
- Il trapezio
- Esempio
- Esercizio in pdf
- Soluzioni esercizio
Cose da sapere
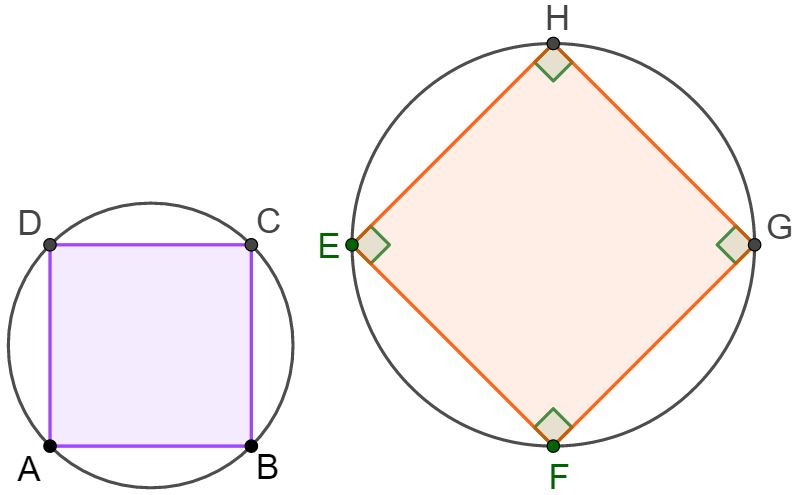
Prima di partire con alcuni esempi per capire quando un quadrilatero è inscrivibile a una circonferenza, bisogna sapere cosa vuol dire inscrivibile. La cosa migliore è dare un’occhiata all’ immagine sotto.
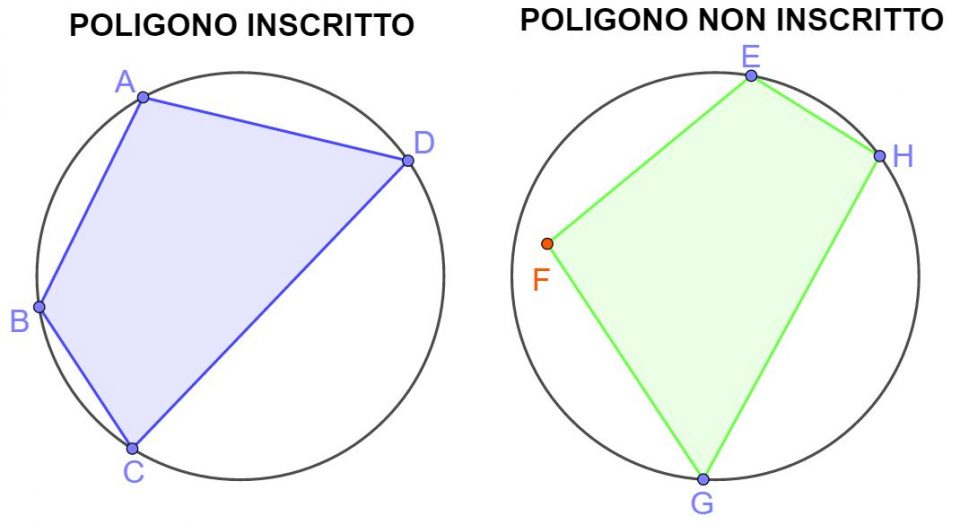
Osserviamo attentamente i due quadrilateri. Quello a sinistra, cioè quello di colore celeste, cioè il quadrilatero ABCD è inscritto alla circonferenza perchè tutti i suoi vertici toccano la circonferenza (probabilmente la tua prof ha detto: “tutti i vertici del quadrilatero giacciono sulla circonferenza oppure appartengono alla circonferenza).
Invece la figura a destra, cioè il quadrilatero EFGH non è inscritto alla circonferenza perchè i suoi vertici non toccano tutti la circonferenza, infatti il vertice F non tocca la circonferenza (la tua prof probabilmente ha detto :“il vertice F non appartiene alla circonferenza oppure non giace sulla circonferenza”.
Piccolo esercizio
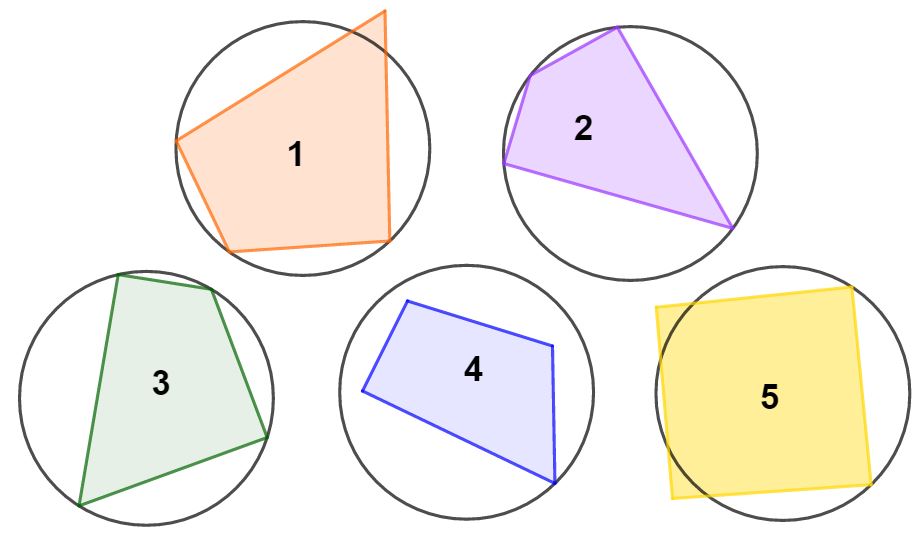
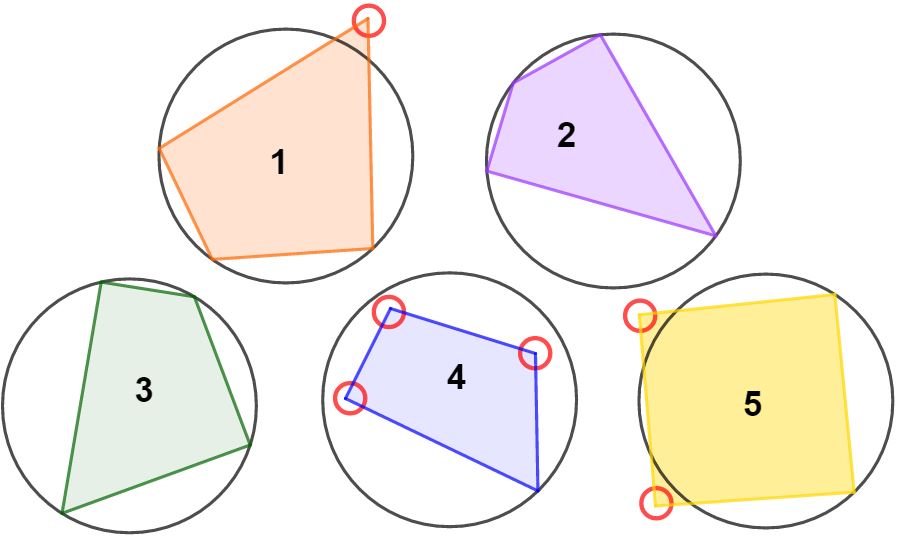
Prima di andare avanti, facciamo un piccolo esercizio per sicuri di aver capito quando un quadrilatero è inscritto in una circonferenza. Osserva l’immagine in basso e stabilisci quali sono i quadrilateri inscritti in una circonferenza. Trovi la risposta alla fine dell’articolo.
Criterio per capire se un quadrilatero è inscrivibile in una circonferenza
Molto bene, dopo avere capito cosa vuol dire “inscritto in una circonferenza”, cerchiamo di capire se un qualsiasi quadrilatero può essere inscritto oppure no in una circonferenza. Infatti ci sono alcuni quadrilateri che possono essere inscritti e altri che non lo possono essere. Per capire meglio quello che hai appena letto, guardiamo la figura in basso.
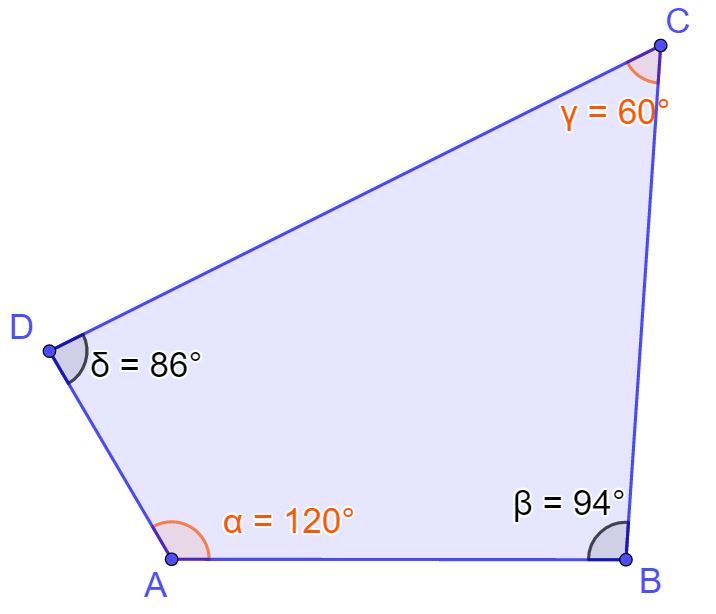
Quello in figura è un poligono che ha 4 lati, quindi è un quadrilatero. Come puoi vedere sono segnate le ampiezze dei lati. Sono proprio gli angoli che ci permettono di capire se un quadrilatero è inscrivibile in una circonferenza. In particolare gli angoli opposti. Nel quadrilatero dell’esempio, gli angoli opposti sono:
α e γ (alfa e gamma)
e poi
β e δ (beta e delta)
Per capire se un quadrilatero è inscrivibile in una circonferenza bisogna addizionare gli angoli opposti. Se la somma delle loro ampiezze dà 180°, allora il quadrilatero è inscrivibile.
Verifichiamo se il quadrilatero del nostro esempio è inscrivibile. Addizioniamo due angoli opposti.
α + γ = 120° + 60° = 180° → il quadrilatero è inscrivibile.
Espressa in un altro modo la regola dice:
“Un quadrilatero è inscrivibile a una circonferenza se gli angoli opposti sono supplementari”
Andiamo a disegnare la circonferenza.
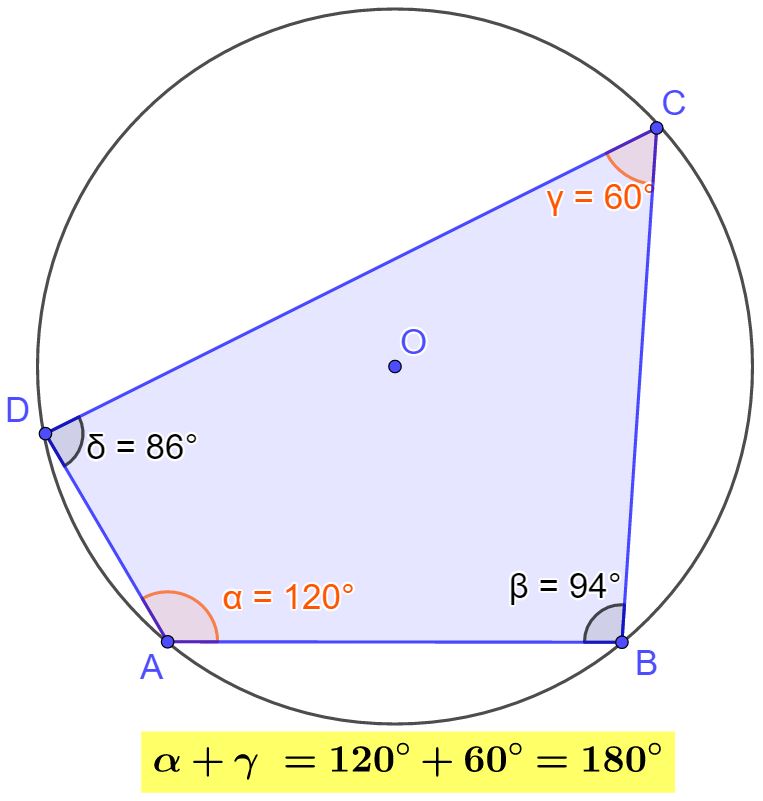
Il punto O è il centro della circonferenza. La circonferenza tocca tutti i vertici del quadrilatero, quindi il quadrilatero ABCD è inscritto alla circonferenza.
Poligoni particolari
Tenendo presente la regola (somma degli angoli opposti = 180°) cerchiamo di capire se i quadrilateri che si usano più spesso a scuola (rettangolo, quadrato, parallelogramma, rombo, trapezio isoscele) sono inscrivibili in una circonferenza oppure no.
Il rettangolo
Il rettangolo può sempre essere inscritto in una circonferenza. Qualsiasi sia il rettangolo che disegni, lo puoi sempre inscrivere in una circonferenza. Facciamo alcuni esempi.
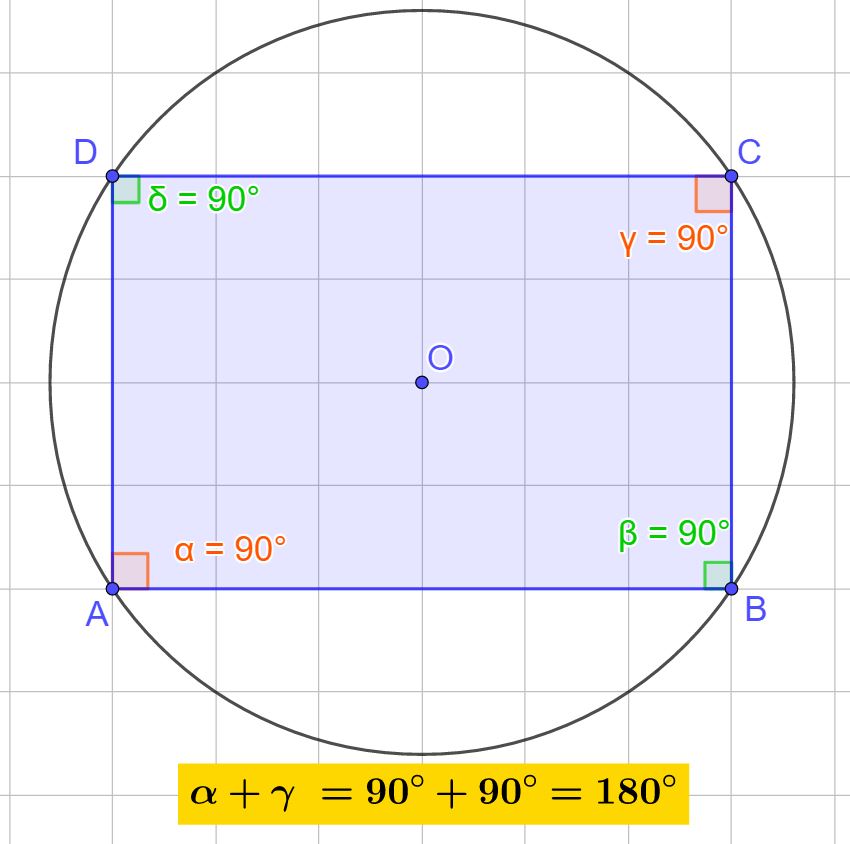
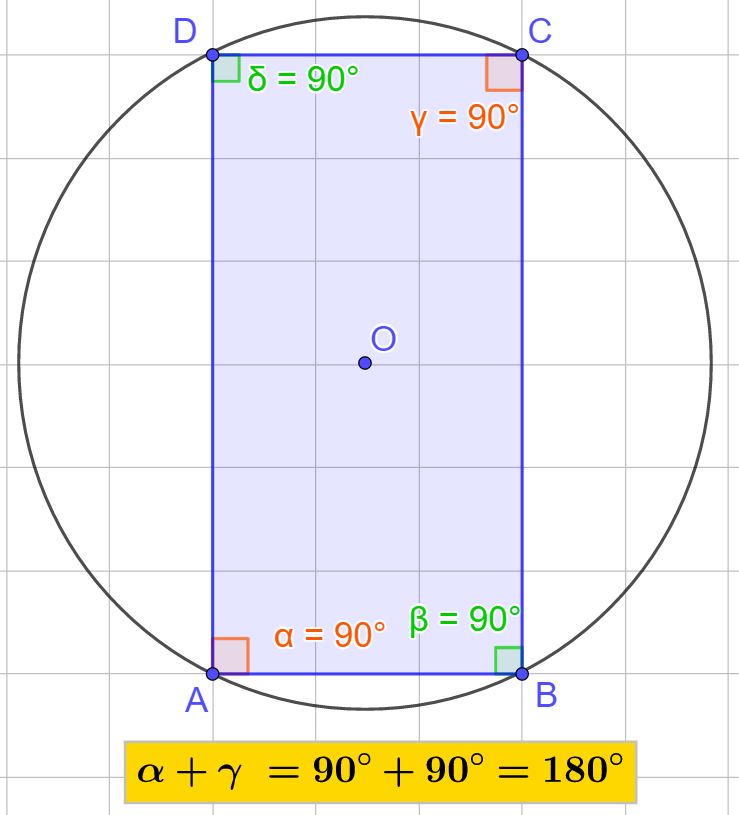
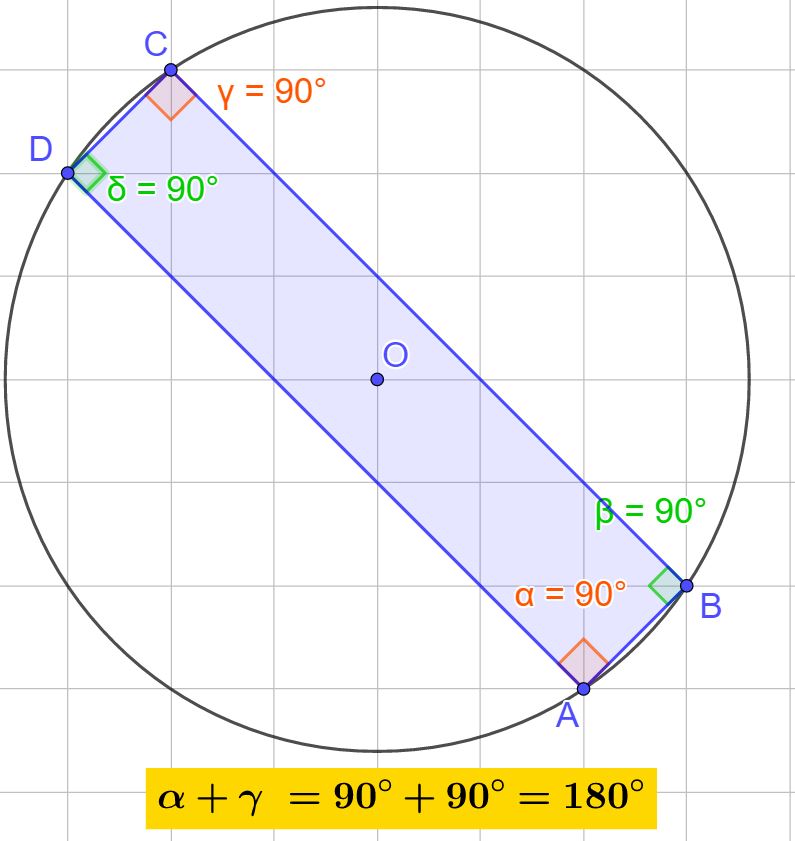
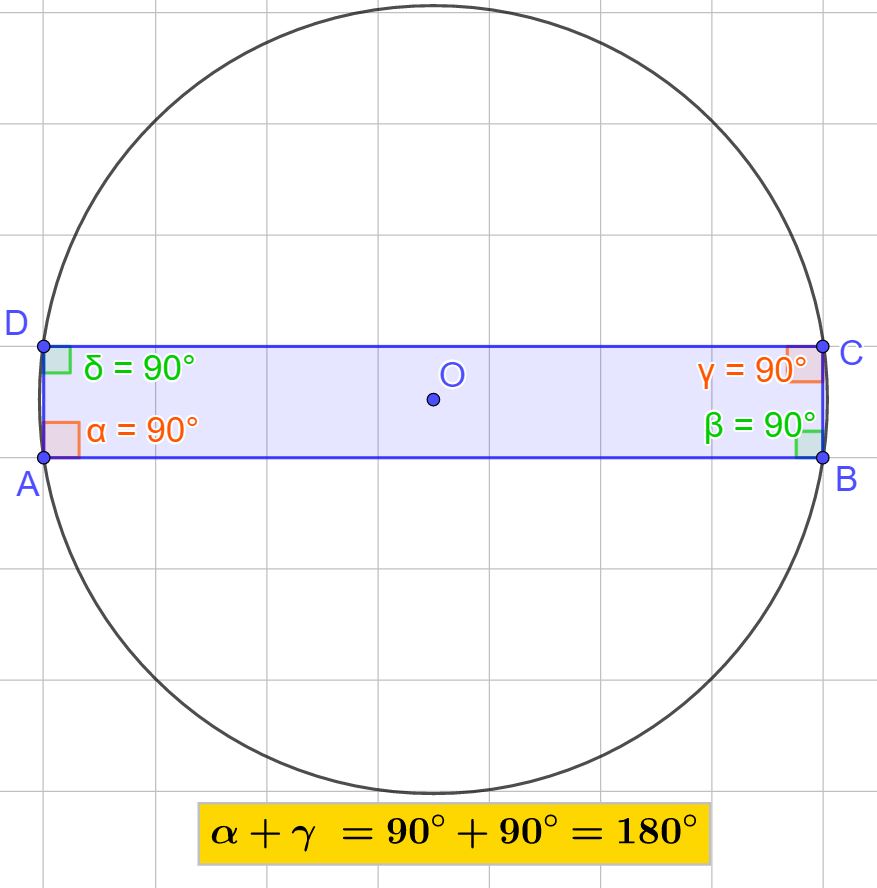
Se ci fermiamo un attimo a ragionare, ci appare chiaro il motivo che ci permette di inscrivere sempre un rettangolo in una circonferenza. Per definizione il rettangolo ha tutti e 4 gli angoli retti (altrimenti non sarebbe un rettangolo). Se addizioniamo due angoli opposti, che saranno tutti e due retti, otterremo come risultato sempre 180°, infatti:
90°+ 90° = 180°
E questo è vero per qualsiasi rettangolo.
Il quadrato
Lo stesso discorso fatto per il rettangolo, vale anche per il quadrato. Anche questo quadrilatero può sempre essere inscritto in una circonferenza. Vediamo alcuni esempi nelle immagini sotto.
Anche nei quadrati gli angoli opposti sono sempre supplementari visto che tutti gli angoli sono retti.
Il parallelogramma
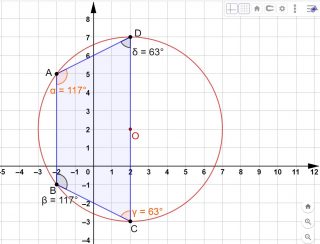
Vediamo ora di capire se un qualsiasi parallelogramma è inscrivibile in una circonferenza. Ti ricordo che il parallelogramma è quel quadrilatero che ha i lati opposti paralleli, ma non ha angoli retti, come quello che vedi in basso.
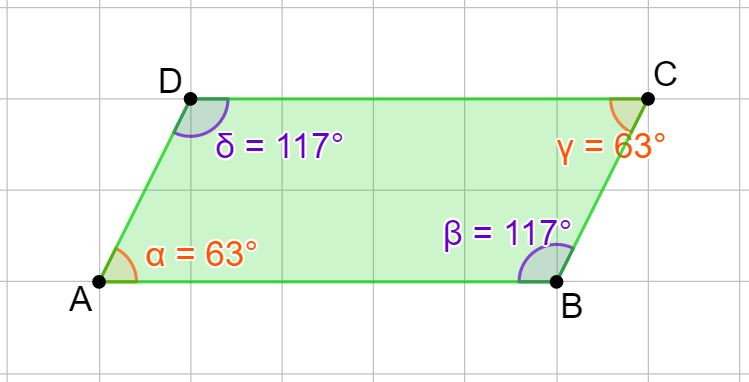
Ti ricordo che per capire se un quadrilatero è inscrivibile in una circonferenza si devono addizionare gli angoli opposti. Nel nostro parallelogramma gli angoli opposti sono quelli di colore arancione
α e γ → angoli opposti (entrambi acuti)
e anche quelli di colore viola
β e δ → angoli opposti (entrambi ottusi)
Proviamo ad addizionarili:
α + γ = 63° + 63° = 126° → non 180°, quindi non è inscrivibile
Nei parallelogrammi gli angoli opposti sono o entrambi acuti, oppure entrambi ottusi. Quindi la somma degli angoli opposti in un parallelogramma non darà mai come risultato 180°. Questo vuol dire che nessun parallelogramma è inscrivibile in nessuna circonferenza.
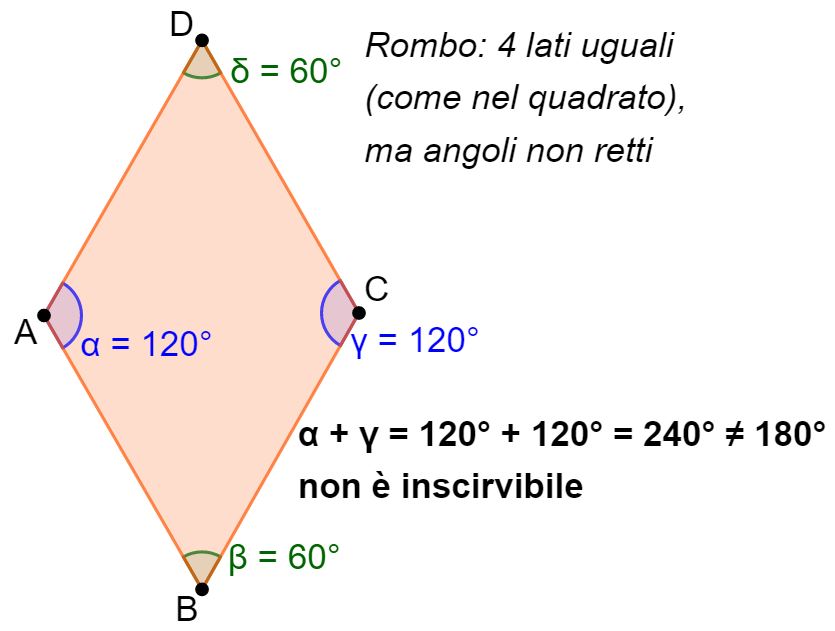
Il rombo
Lo stesso discorso fatto per il parallelogramma, vale il rombo. In qualsiasi rombo, gli angoli opposti sono o tutti e due acuti oppure tutti e due ottusi. Quindi nessun rombo sarà mai inscrivibile in una circonferenza.
La figura in basso illustra quello che hai appena letto.
Il trapezio isoscele
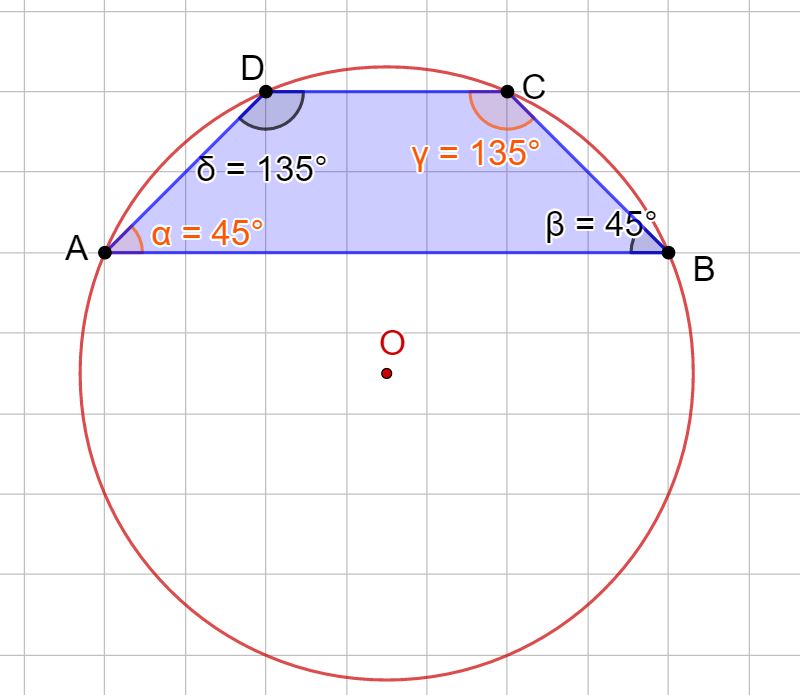
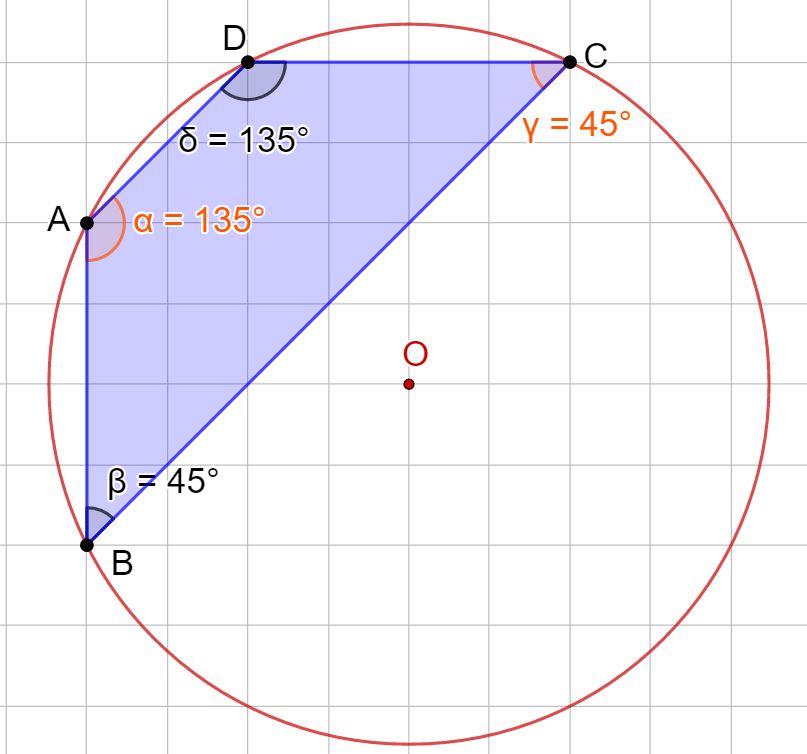
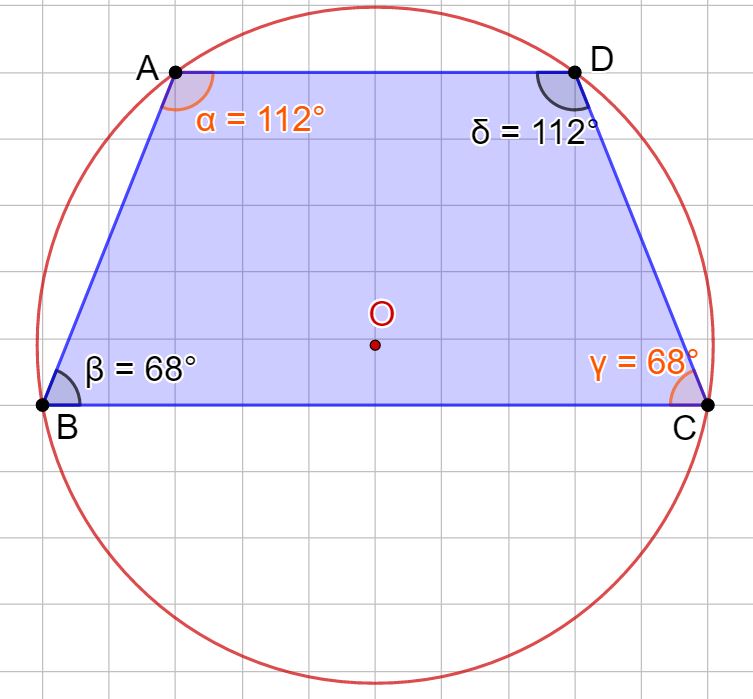
Tra i trapezi (isoscele, rettangolo e scaleno) solo quello isoscele è sempre inscrivibile in una circonferenza. Invece trapezio rettangolo e trapezio scaleno non lo sono mai.
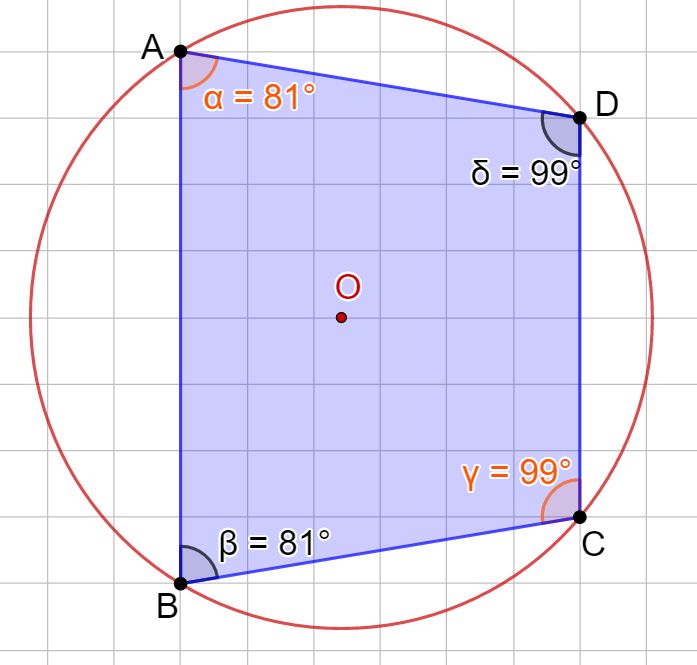
Esempio
Adesso guardiamo la figura in basso e cerchiamo di capire se il quadrilatero è inscrivibile in una circonferenza.
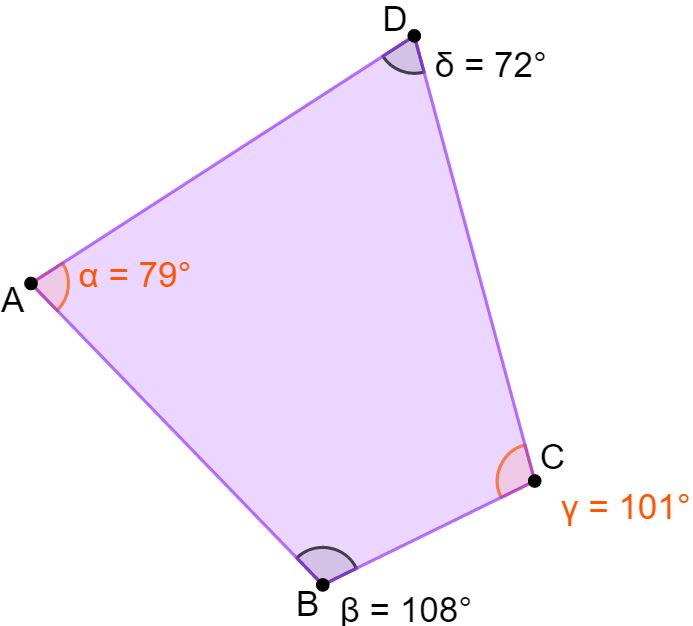
Ormai hai imparato che dobbiamo sommare gli angoli opposti.
α + γ = 79° + 101° = 180° → il quadrilatero è inscrivibile
Andiamo a disegnare la circonferenza.
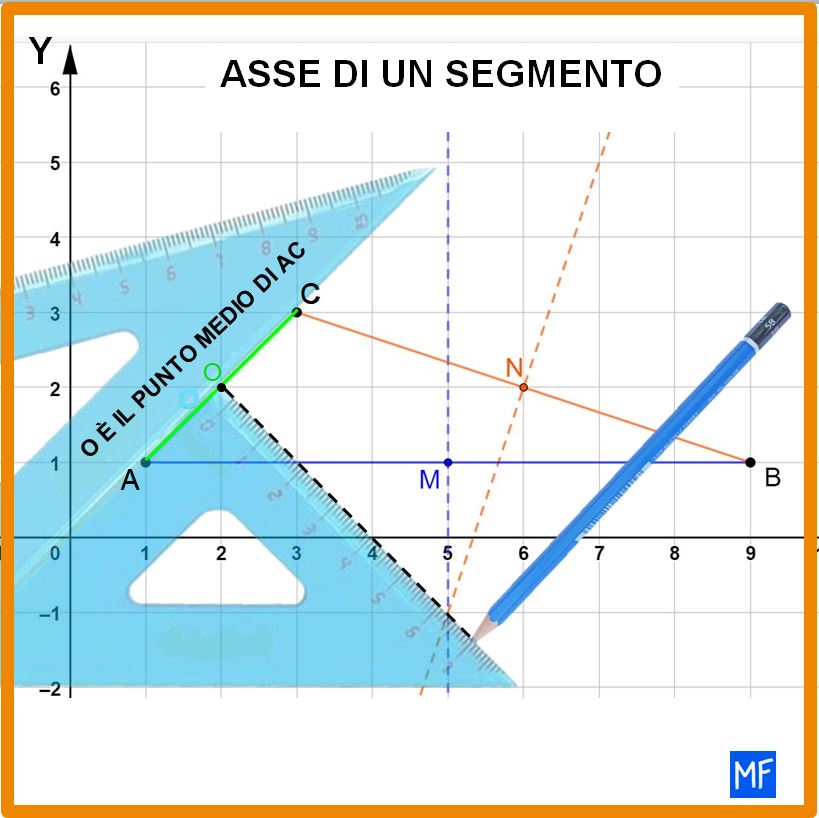
Per disegnare la circonferenza usando il compasso devi prima tracciare l’asse di ogni lato. Se non ti ricordi come si traccia un asse potresti leggere il mio articolo: tracciare l’asse di un segmento. Vedrai che i 4 assi si incontrano in un unico punto. Quello sarà il centro della circonferenza.
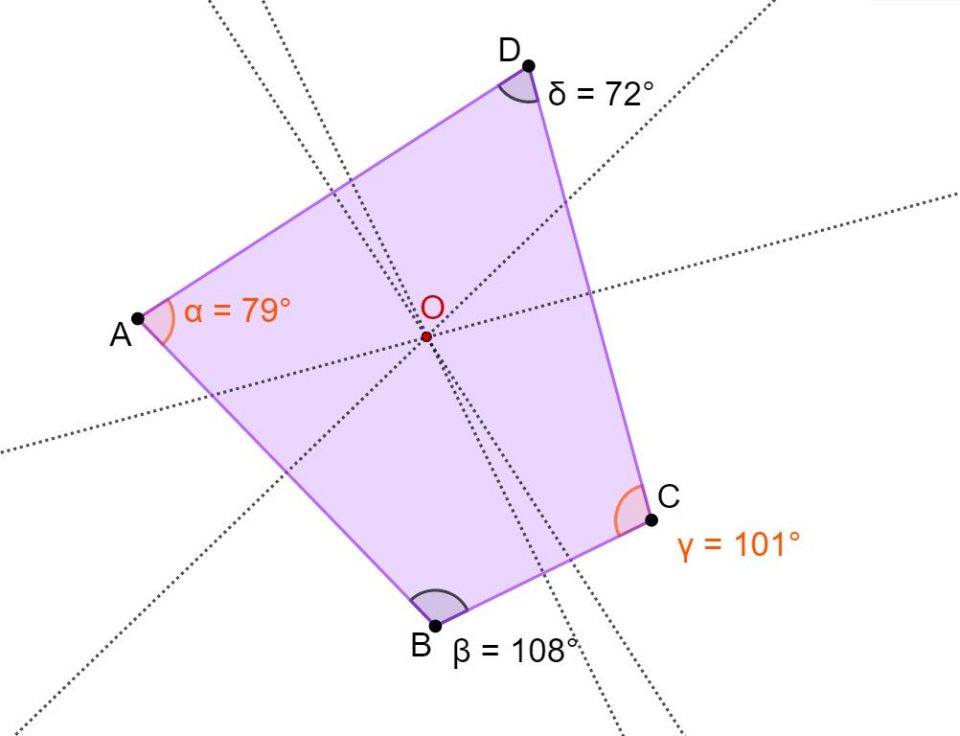
Se usi il compasso, dovrai puntare il compasso in O, e l’apertura deve essere OA. Tracciando la circonferenza otterrai un risultato come quello che vedi in basso.
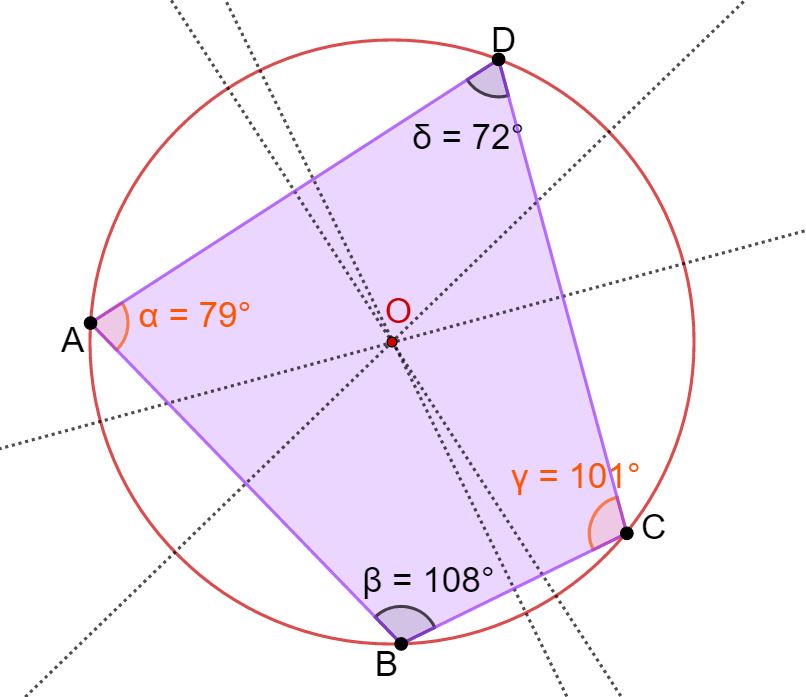
Vedi come la circonferenza tocca tutti e 4 i vertici del quadrilatero. Quindi il quadrilatero è inscritto nella circonferenza. Se la vogliamo dire in modo diverso, la circonferenza è circoscritta al quadrilatero e il punto O è chiamato circocentro.
Esercizio in pdf
Adesso se vuoi puoi metterti alla prova con l’esercizio che trovi nel file pdf in basso. Lavora senza fretta e non ti proeccupare se sbagli. Sbagliando si impara. Trovi il grafico con il disegno alla fine dell’articolo.
![]() Quadrilatero inscrivibile – Esercizio.pdf
Quadrilatero inscrivibile – Esercizio.pdf
Buon lavoro.
Risposta al piccolo esercizio
I poligoni inscritti sono il numero 2 e il numero 3. Infatti solo in questi due quadrilateri tutti i vertici toccano la circonferenza.
- Nel numero 1, uno dei vertici è esterno alla circonferenza.
- Nel numero 4, solo uno dei vertici tocca la circonferenza, ma gli altre 3 no.
- Nel numero 5 solo due vertici toccano la circonferenza, ma gli altri due no.
risultato esercizio
Per tracciare le figure geometriche è stato usato il software GeoGebra che è gratis e liberamente scaricabile dal sito ufficiale di GeoGebra.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.