Se sei arrivato in questa pagina vuol dire che forse hai qualche difficoltà con gli esercizi che ha assegnato la tua prof di matematica. Gli esercizi riguardano le espressioni con le frazioni e le potenze. Niente paura, con 5 minuti di impegno ti sarà tutto più chiaro.
Indice
Cose da sapere
Non ti farò false promesse, per sapere eseguire le espressioni con le frazioni e le potenze è prima necessario sapere alcune cose:
Dopo che avrai capito questi due argomenti, potrai passare alle espressioni con frazioni e potenze che, come dice il nome stesso, riuniscono in un solo esercizio sia le frazioni, sia le potenze. Lo so che può essere un po’ difficile, ma non puoi costruire il terzo piano di una casa se prima non hai costruito il primo e il secondo piano.
Esempio 1
Cominciamo con qualche esempio numerico per capire come si eseguono le espressioni con potenze e frazioni. Partiremo da espressioni facili e poi pian piano arriveremo a espressioni più difficili. Eseguiamo cinque sesti meno un quarto tutto al quadrato.

Anche in queste espressioni ci sono delle precedenze da rispettare:
- prima si eseguono le operazioni dentro le parentesi (tonde, quadre e graffe),
- poi si eseguono le potenze,
- poi moltiplicazioni e divisioni da sinistra a destra e
- poi addizioni e sottrazioni da sinistra a destra.
In questo esempio abbiamo solo parentesi tonde. All’interno delle parentesi c’è solo una sottrazione tra frazioni che si risolve calcolando il minimo comune multiplo tra i denominatori. Se non ti ricordi come si calcola il minimo comune multiplo potresti dare un’occhiata al mio articolo: il minimo comune multiplo.
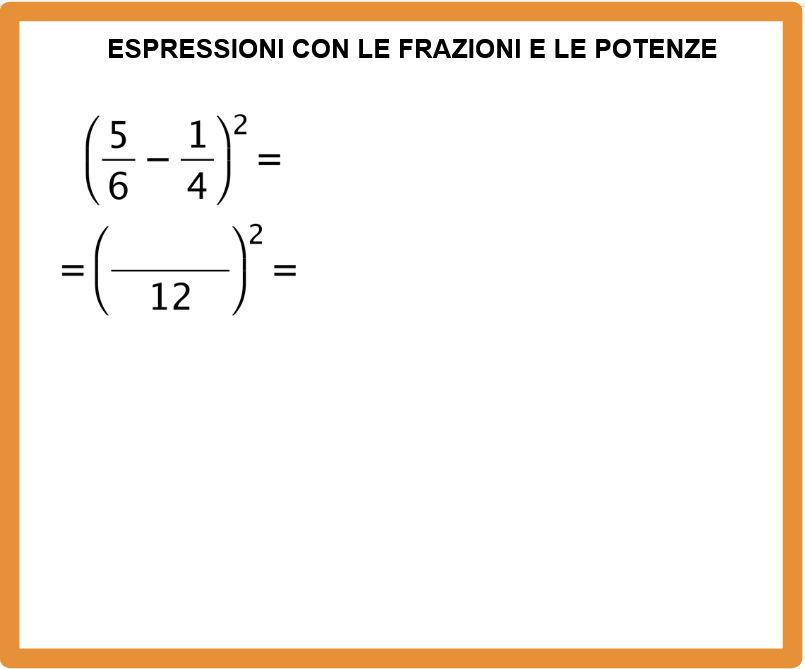
Dato che prima dobbiamo eseguire le operazioni dentro le parentesi, possiamo riscrivere le parentesi e scriviamo anche l’esponente (cioè il 2 piccolino in alto a destra).
Il minimo comune multiplo tra 4 e 6 è 12. Lo scriviamo al denominatore della frazione. Adesso procediamo eseguendo la sottrazione tra frazioni, se vuoi andare a ripassare come si fa, potresti dare un’occhiata al mio articolo addizioni e sottrazioni tra frazioni.
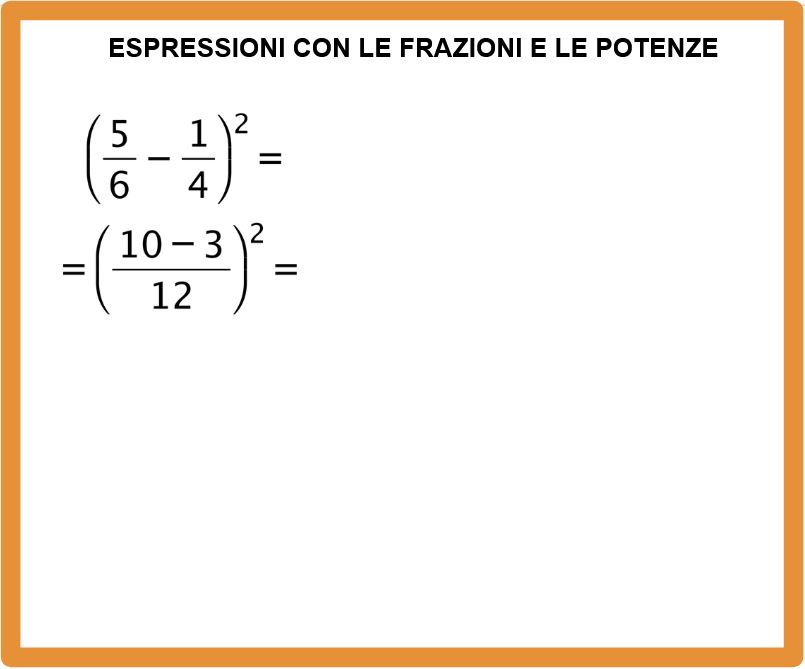
Adesso eseguiamo la sottrazione al numeratore, cioè 10-3 e otteniamo come risultato 7 che scriviamo al numeratore.

Benissimo, adesso dobbiamo eseguire la potenza di una frazione, se vuoi puoi ripassare la potenza di una frazione leggendo questo articolo: la potenza di una frazione.
Elevare alla seconda sette fratto dodici, vuol dire eseguire una moltiplicazione in cui la frazione sette dodicesimi si moltiplica due volte.
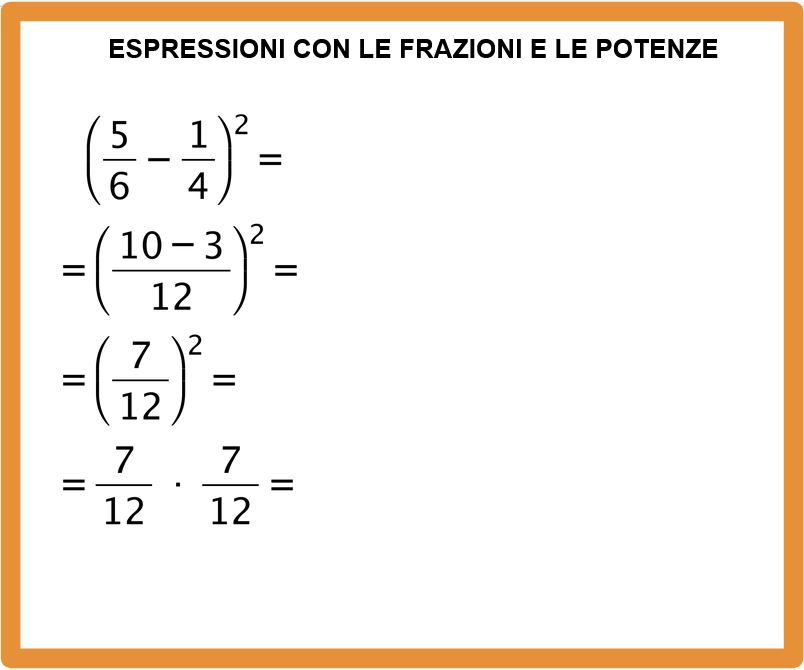
Dobbiamo moltiplicare numeratore per numeratore e denominatore per denominatore.

Benissimo, abbiamo ottenuto la frazione quarantanove fratto centoquarantaquattro. Abbiamo concluso.
Esempio 2
Passiamo ora ad un altro esempio per essere sicuri di avere capito come si eseguono le espressioni con le frazioni e le potenze. Usiamo gli stessi numeri dell’esempio precedente, ma con le parentesi posizionate in modo diverso. Questo ci aiuterà a capire l’importanza delle parentesi.
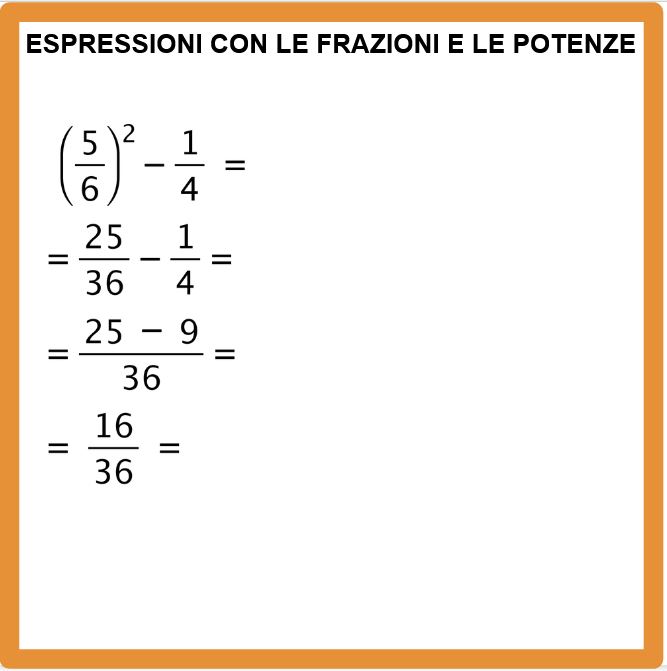
Eseguiamo l’espressione: cinque sesti tutto al quadrato, meno un quarto.

In questo esempio la prima cosa da fare è la potenza, perchè all’interno delle parentesi tonde non abbiamo altre operazioni.
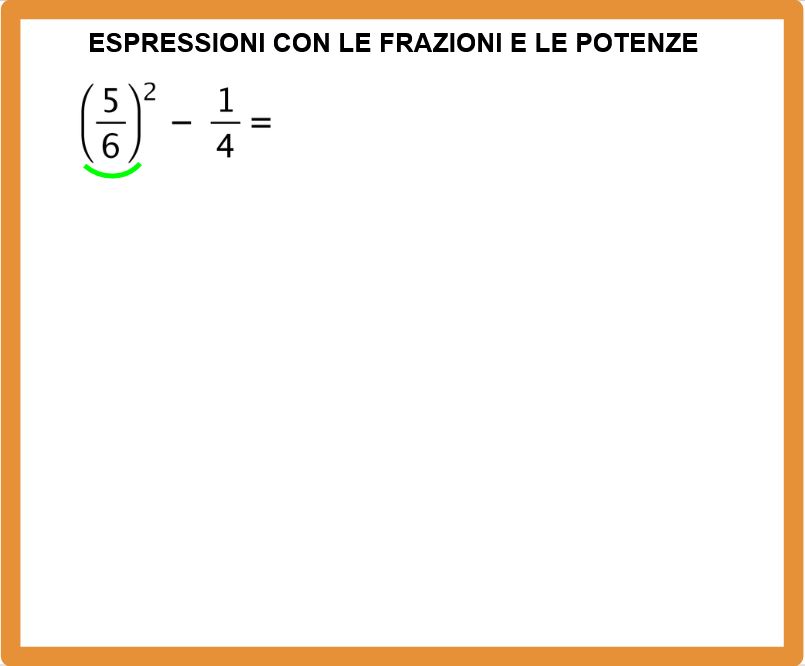
Cinque sesti elevato a due (si può anche dire elevato al quadrato) è uguale a venticinque trentaseiesimi. E poi riscriviamo meno un quarto.
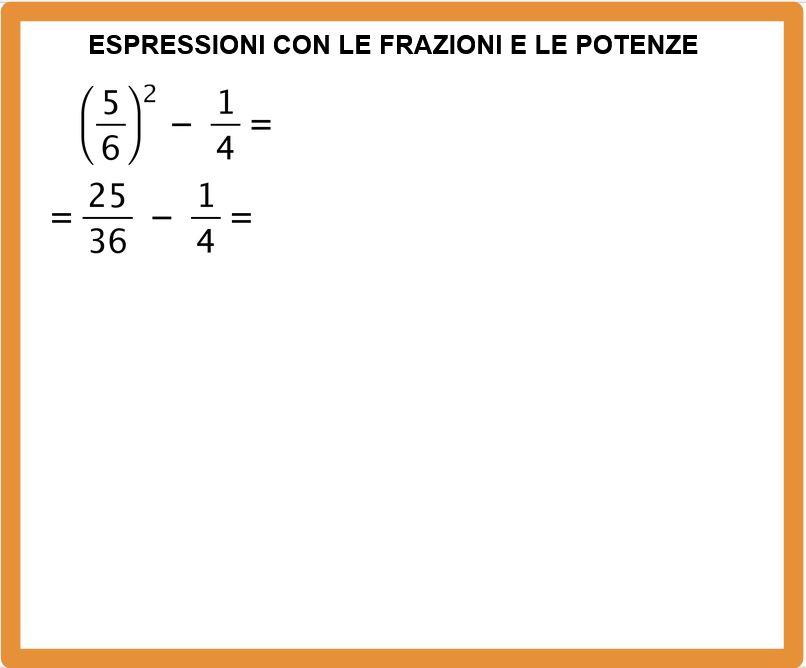
Adesso dobbiamo calcolare il minimo comune multiplo tra i denominatori 36 e 4 e procedere con la sottrazioni tra frazioni.
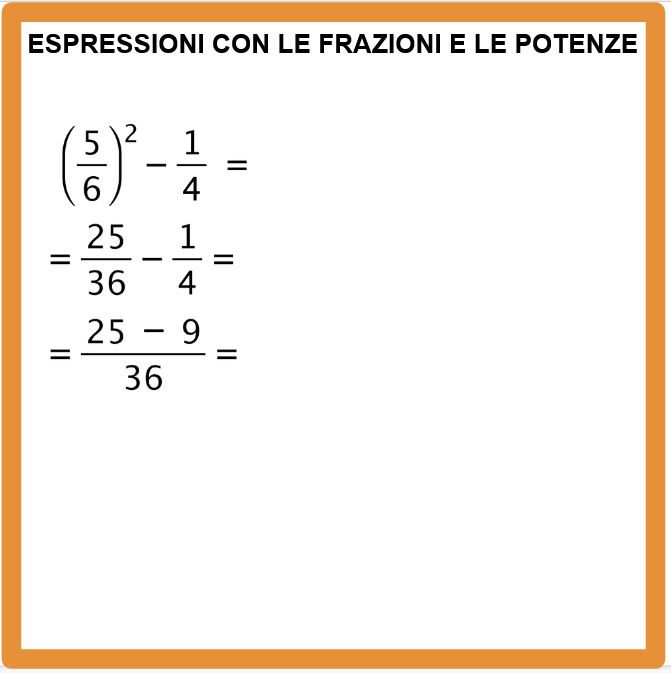
Molto bene, ora eseguiamo la sottrazione che compare al numeratore 25-9 e otteniamo la frazione sedici fratto trentasei.
Non abbiamo ancora finito. Infatti, quando è possibile si deve sempre ridurre ai minimi termini. Se non ti ricordi come si riduce ai minimi termini, potresti leggere il mio articolo: ridurre una frazione ai minimi termini. Usiamo come fattore di riduzione 4.

Benissimo. Dividendo sia il numeratore che il denominatore per 4 otteniamo la frazione quattro noni.

Perfetto. Abbiamo concluso. Il risultato che stavamo cercando è quattro noni.
Esempio 3
Facciamo ancora un altro esempio per essere sicuri di avere capito come si eseguono le espressioni con le potenze e le frazioni. Andiamo un po’ più veloci. Quello che devi ricordare è di rispettare le precedenze e devi ricordarti come si eseguono le divisioni tra frazioni. Se non te lo ricordi puoi dare un’occhiata al mio articolo: divisione tra frazioni.

Non è semplice, lo so. Non ho mai detto che sarebbe stato facile, ma ce la puoi fare, non ti arrendere. Per riuscire a eseguire le espressioni con le frazioni e le potenze si devono conoscere altri argomenti. Prova e riprova. L’impegno prima o poi verrà ripagato.
Ecco l’espressione con una breve descrizione delle operazioni svolte.

È possibile eseguire qualche passaggio in meno. Con un’espressione come quella dell’esempio è possibile seguire strade diverse, cioè eseguire qualche passaggio in più o in meno. Qualunque sia la strada che scegli, si deve però arrivare allo stesso risultato. Se ottieni un risultato diverso, vuol dire che da qualche parte c’è un errore. Non mollare, non arrenderti, riprova e ce la farai.
Esercizi in pdf
Adesso se vuoi, puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto. Lavora con calma, non preoccuparti se sbagli. Sbagliare è normale, è sbagliando che si impara. Non arrenderti e riprova 😉.
![]() Espressioni con frazioni e potenze – Esercizi.pdf
Espressioni con frazioni e potenze – Esercizi.pdf
Buon lavoro.
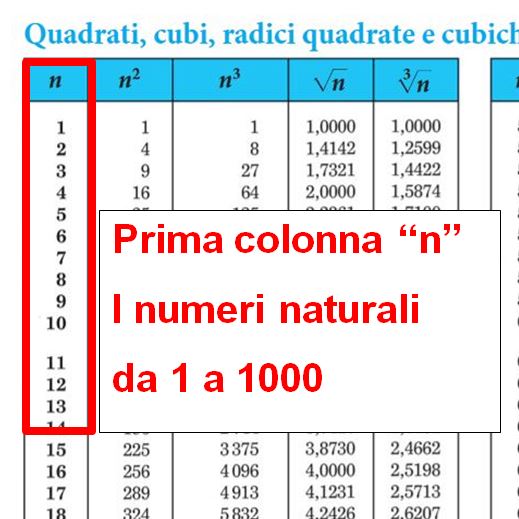
Cliccando qui si aprirà una nuova pagina della Casa Editrice Zanichelli in cui potrai consultare o scaricare le tavole numeriche.
Se vuoi porre domande o vuoi segnalare un errore, puoi scrivere alla casella mail: matematica.facile@libero.it oppure contattarci attraverso le nostre pagine social; saremo grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.
Questo articolo è stato scritto dopo la richiesta di una nostra lettrice, alla quale va il nostro ringraziamento.
Tutto lo staff lavora alacremente per rispondere al meglio alle richieste che riceviamo.
Ci scusiamo per eventuali ritardi.
Lo staff di MF