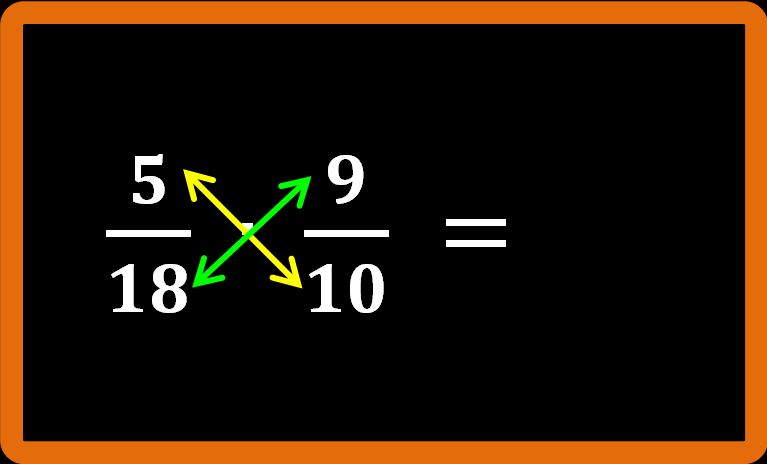Oggi con la prof di matematica avete iniziato un nuovo argomento: la moltiplicazione tra frazioni e la semplificazione in croce. In classe ti era sembrato di avere capito quello che la prof aveva spiegato, ma quando sei tornato a casa, ti sei reso conto di non saper svolgere gli esercizi assegnati. Niente paura, con un po’ di impegno e 5 minuti di tempo, riuscirai a capire come si esegue una moltiplicazione tra frazioni e cosa è la semplificazione in croce.
Dopo aver imparato come si eseguono le moltiplicazioni vedremo come si ottiene la frazione inversa a un’altra frazione. In questo modo avrai tutti le conoscenze per sapere eseguire una divisione tra frazioni e anche la potenza di una frazione. Ma andiamo con ordine.
Indice
- Primo esempio : moltiplicazione tra 2 frazioni
- Secondo esempio : moltiplicazione tra 2 frazioni
- Terzo esempio : moltiplicazione tra 2 frazioni
- Quarto esempio : moltiplicazione tra 3 frazioni
- Quinto esempio : semplificazione in croce
- Esercizi
- Su Youtube
- Esercizi in pdf
- Un altro esempio di moltiplicazione in croce
Piccola premessa
Partiamo subito con un esempio numerico, però prima è meglio fare una breve premessa.

La prof ti avrà sicuramente spiegato che il segno della moltiplicazione si può scrivere sia con un per (x), sia con un puntino ( • ). Sarebbe meglio abituarsi a usare il puntino e ti spiego subito perchè. Andando avanti, forse già alla fine della seconda media, studierete le equazioni. Nelle equazioni oltre ai numeri, si usano anche le lettere come a, b, c, x e y. Quindi si corre il rischio di scambiare la lettera x per il segno x della moltiplicazione. Per questo motivo da ora in poi per scrivere il segno della moltiplicazione useremo il puntino ( • ), che nel nostro caso va messo alla stessa altezza della linea di frazione.
Esempio 1: moltiplicazione tra due frazioni
Partiamo con il primo esempio.
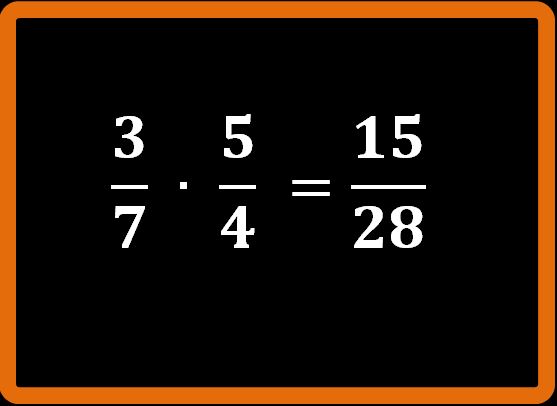
Guardando l’esempio, molto probabilmente ti sei già fatto un’ idea di come si esegue una moltiplicazione tra frazioni. Per trovare il numeratore, bisogna moltiplicare tra loro i numeratori. Per trovare il denominatore, bisogna moltiplicare tra loro i denominatori.
Le operazioni che andremo a eseguire quindi sono:
3 · 5 = 15 (numeratore) e 7 · 4 = 28 (denominatore)
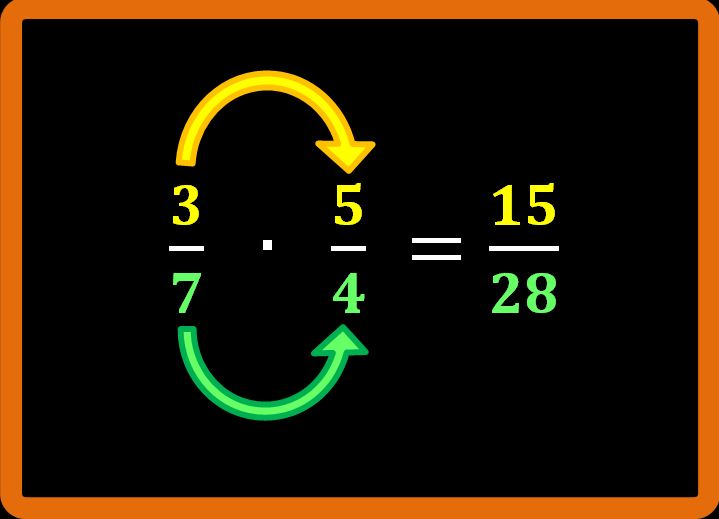
Il risultato che stavamo cercando è 15 su 28 (quindici ventottesimi). Siccome il risultato è già ridotto ai minimi termini, abbiamo concluso. Se non ti ricordi cosa vuol dire ridurre una frazione ai minimi termini, potresti dare un’occhiata al mio articolo come si riduce una frazione ai minimi termini.
Esempio 2: moltiplicazione tra due frazioni
Facciamo un altro esempio per vedere se abbiamo capito come si esegue una moltiplicazione tra frazioni e poi enunciamo la regola in un modo più corretto.
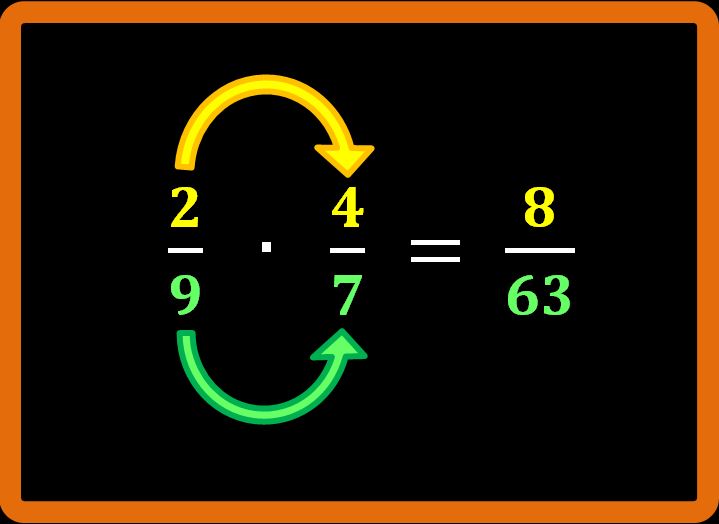
Anche in questo caso il risultato che abbiamo trovato è una frazione che è già ridotta ai minimi termini. Per cui abbiamo concluso l’esercizio.
Enunciamo la regola in modo corretto:
“Il risultato di una moltiplicazione tra frazioni è una frazione che ha come numeratore il prodotto dei numeratori e come denominatore il prodotto dei denominatori.
(È più facile eseguire l’operazione che enunciare la regola.)
È un altro modo per descrivere con le parole quello che abbiamo fatto con i numeri nei nostri due esempi.
Esempio 3: moltiplicazione tra due frazioni
Continuiamo con un altro esercizio:

Le operazioni che dobbiamo eseguire sono:
Per trovare il numeratore 7 · 5 = 35 ;
e per trovare il denominatore 11 · 6 = 66. Quindi il nostro risultato sarà:

Così come per le moltiplicazioni tra i numeri naturali. Anche per le moltiplicazioni tra frazioni vale la proprietà commutativa, cioè cambiando l’ordine dei fattori il prodotto non cambia.
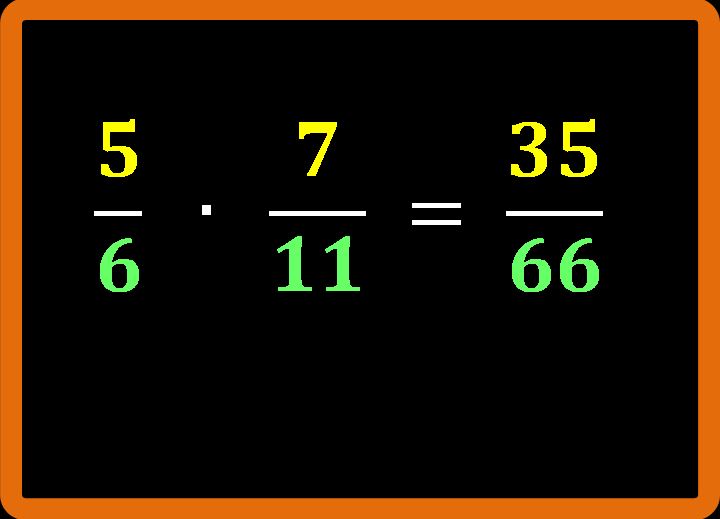
Non è possibile ridurre ai minimi termini. L’esercizio è concluso. (Ricorda che quello che stai imparando in questo articolo ti sarà utile anche quando studierai la potenza di una frazione.)
Esempio 4: moltiplicazione tra 3 frazioni
Anche se le frazioni da moltiplicare sono più di 2, il procedimento è lo stesso. Vediamo un esempio:
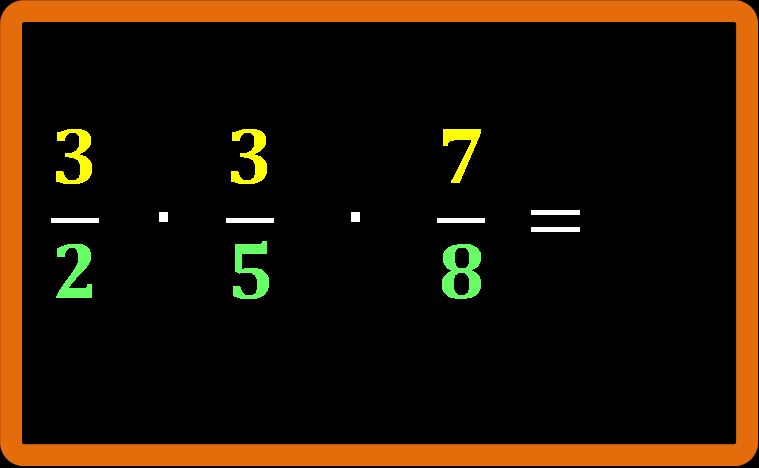
Dobbiamo moltiplicare tra loro i numeratori:
3 · 3 · 7 = 63
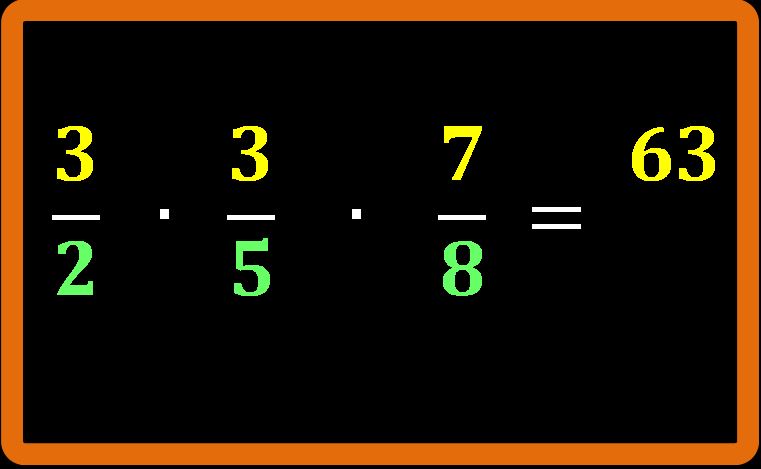
E poi moltiplichiamo tra loro i denominatori:
2 · 5 · 8 = 80
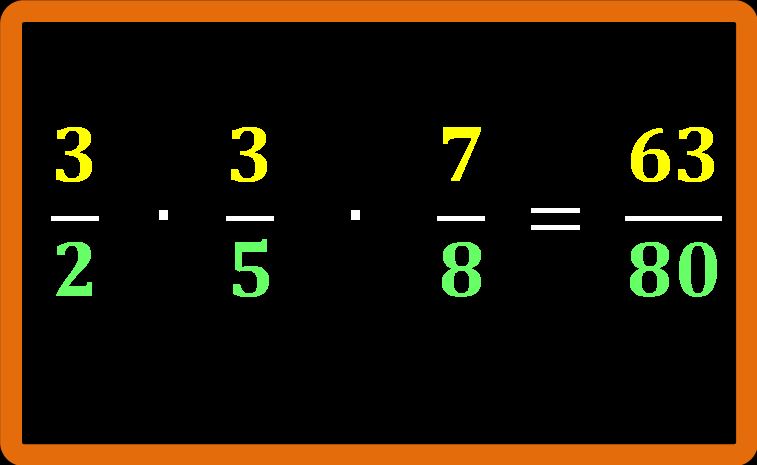
Un altro modo di procedere potrebbe essere applicare la proprietà associativa della moltiplicazione. Cioè, prima si moltiplicano tra loro le prime due frazioni e poi il risultato ottenuto si moltiplica per la terza frazione.
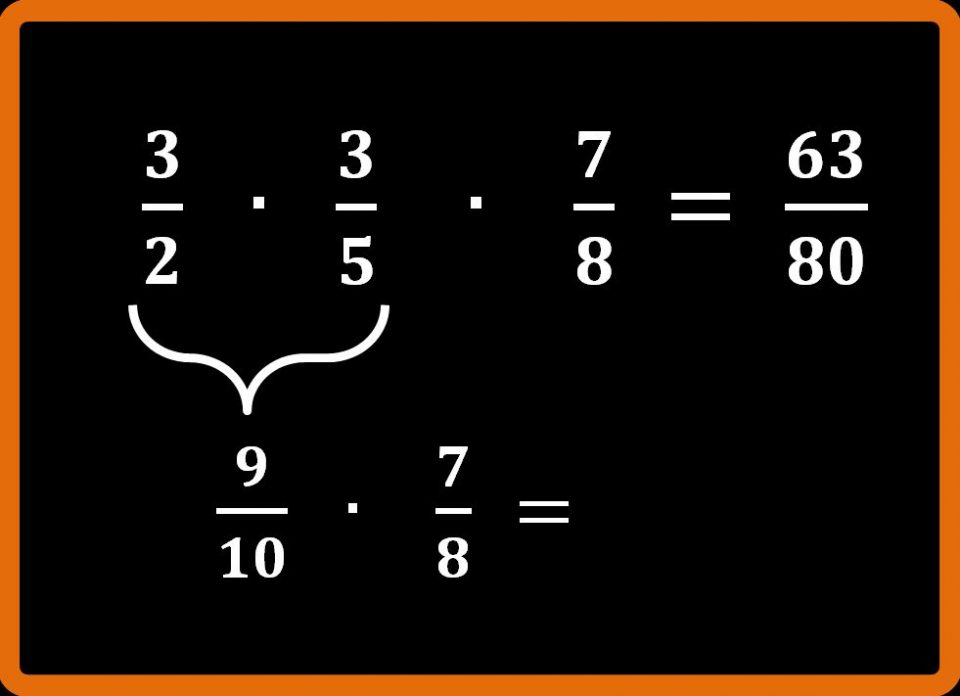
Ora non ci resta che eseguire una moltiplicazione tra due frazioni, che ormai sappiamo svolgere.
Numeratore per numeratore, cioè 9 · 7 = 63
Denominatore per denominatore 10 · 8 = 80
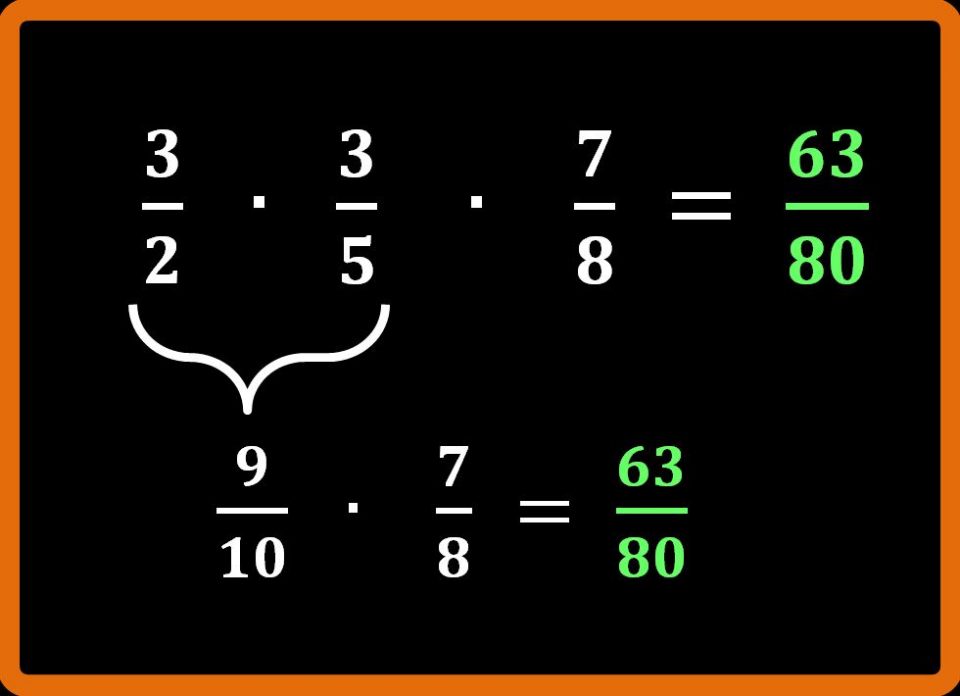
Naturalmente non è importante quale procedimento scegli di seguire. Il risultato deve essere sempre lo stesso per entrambi i procedimenti.
Esempio 5: semplificazione in croce
Continuiamo con un altro esempio che ci permetterà di capire la moltiplicazione tra frazioni e la semplificazione in croce.
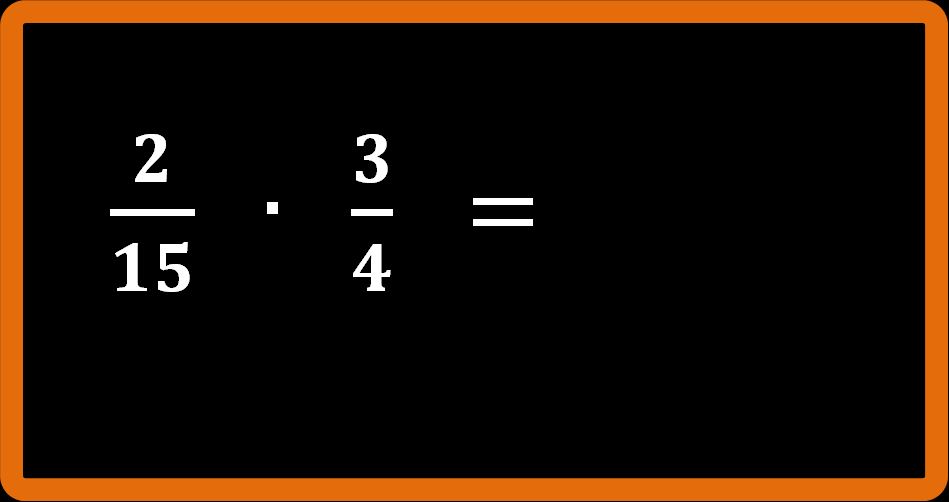
Per eseguire questa moltiplicazione tra frazioni abbiamo due strade:
- Possiamo seguire il procedimento che abbiamo imparato a conoscere (numeratore per numeratore e denominatore per denominatore):
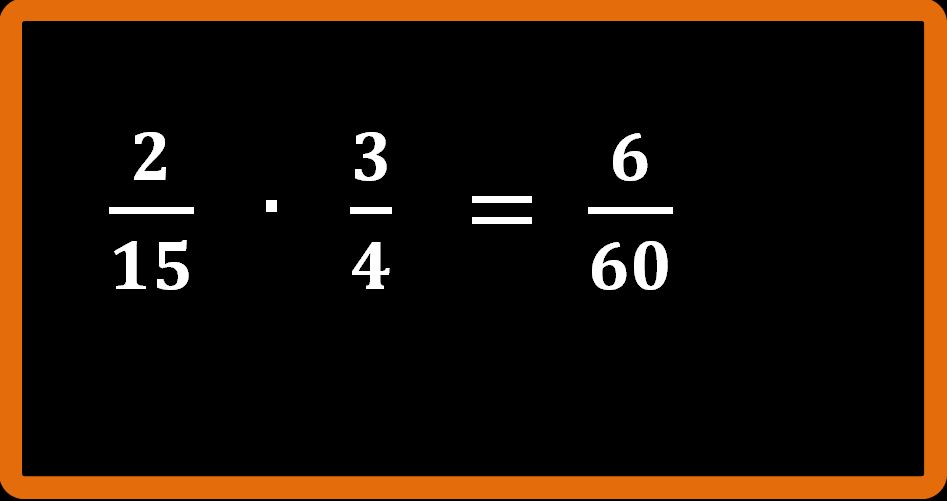
A questo punto però dobbiamo fare attenzione. Non abbiamo finito, dobbiamo ridurre ai minimi termini. È possibile usare diversi fattori di riduzione, il risultato finale deve essere comunque lo stesso.
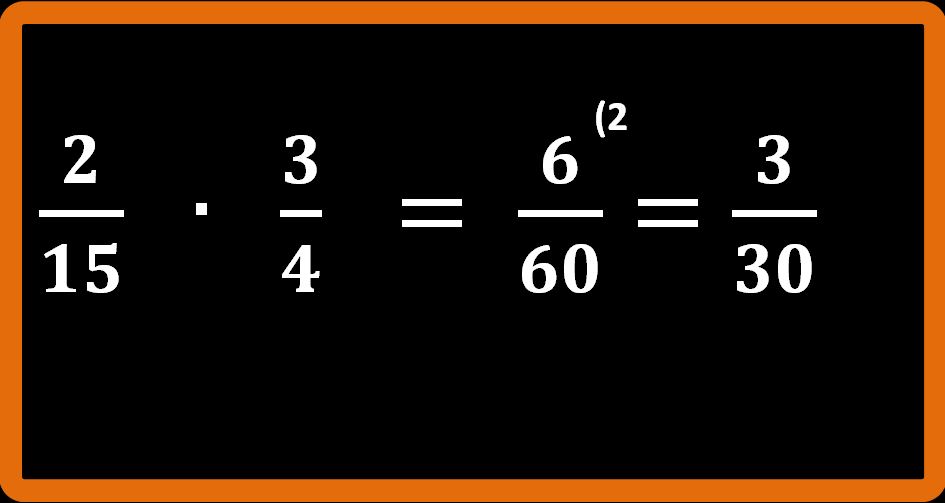
Ma non abbiamo ancora finito. È ancora possibile semplificare.
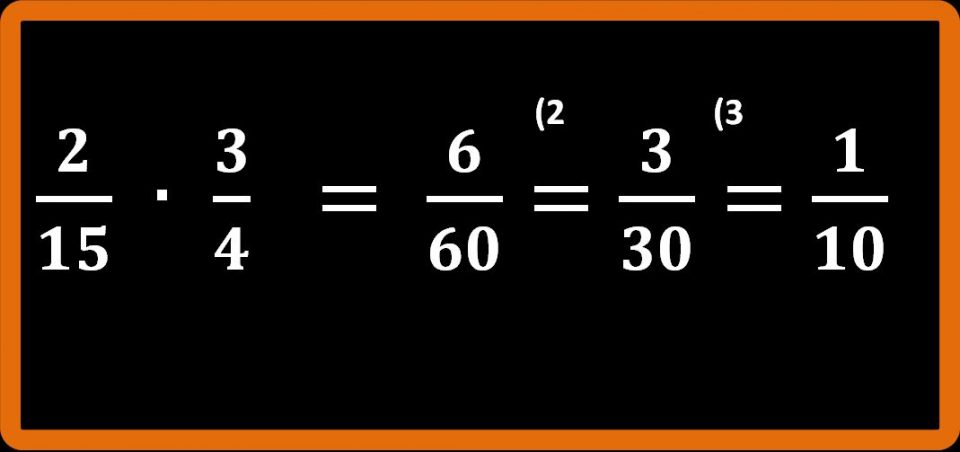
Adesso abbiamo finito. Non è più possibile semplificare. Il risultato che stavamo cercando è 1 su 10, che si può anche leggere un decimo.
2. La seconda strada è semplificare in croce. Noi abbiamo già visto cosa vuol dire semplificare una frazione. Lo ricordiamo: semplificare una frazione vuol dire dividere numeratore e denominatore della frazione per lo stesso numero. La semplificazione in croce è un procedimento molto simile, solo che coinvolge due frazioni. Applichiamo la semplificazione in croce nell’esempio appena eseguito e cerchiamo di capire meglio.
Siamo partiti da questo prodotto:
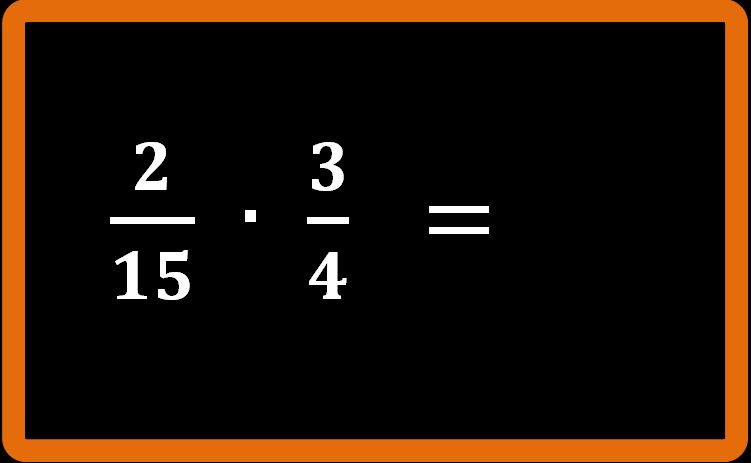
Dobbiamo capire se è possibile dividere il numeratore della prima frazione (2) e il denominatore della seconda frazione (4) per lo stesso numero. È possibile infatti possiamo dividerli per 2. Si scrive così:
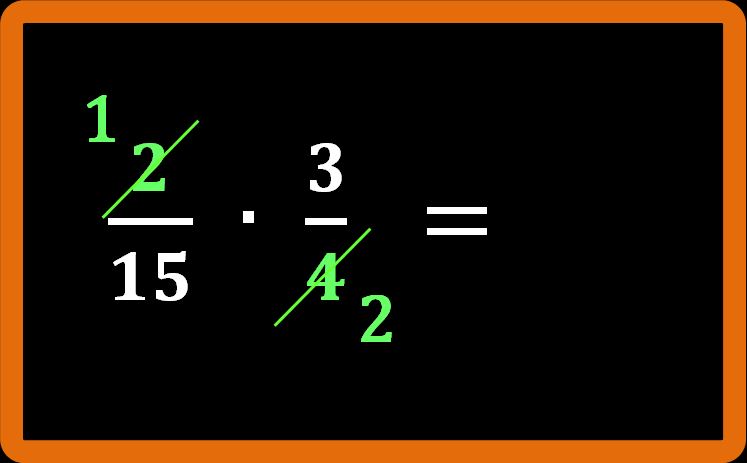
Allo stesso modo, dobbiamo cercare di capire se è possibile dividere il denominatore della prima frazione (15) e il numeratore della seconda frazione (3) per lo stesso numero. L’operazione è possibile, infatti possiamo dividerli per 3. Si scrive così:
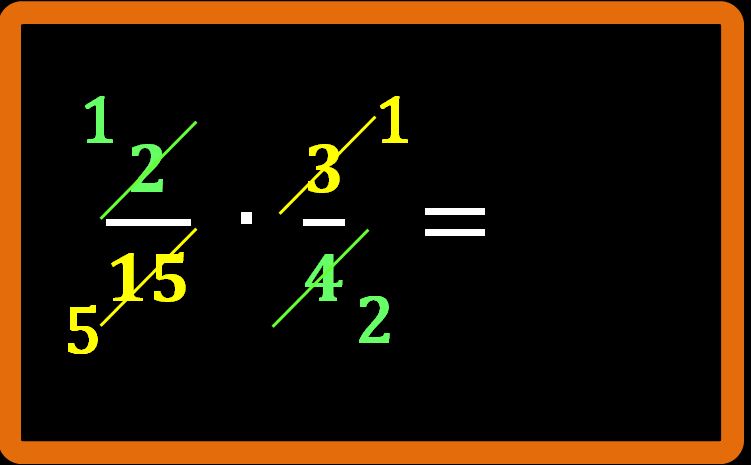
Non possiamo più semplificare. Quello che dobbiamo fare adesso è moltiplicare il numeratore della prima frazione (1) per il numeratore della seconda frazione (1):
1 · 1 = 1
E poi moltiplicare il denominatore della prima frazione (5) per il denominatore della seconda frazione (2):
5 · 2 = 10
Il risultato che otteniamo è il seguente:
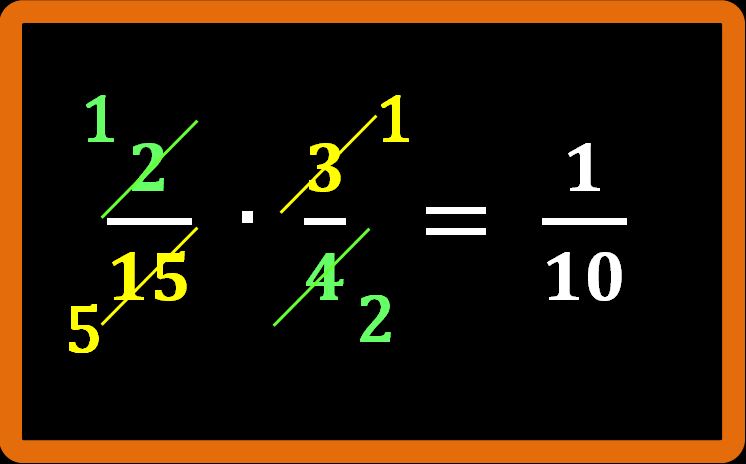
Abbiamo ottenuto 1 su 10 (che si può leggere anche un decimo) che è lo stesso risultato che abbiamo ottenuto con il primo metodo.
So cosa stai pensando. Stai pensando che questo metodo della semplificazione in croce non ti piace e che preferisci il primo metodo. È comprensibile, ma quando ti troverai a moltiplicare quattro frazioni tra loro sarà meglio sapere applicare la semplificazione in croce, altrimenti ti ritroverai a lavorare con numeri molto grandi. E a noi non piacconno i numeri grandi perchè sono difficili da gestire e da maneggiare.
Esercizi
È arrivato il momento di provare da solo. Possiedi tutti gli strumenti necessari per eseguire in modo corretto gli esercizi che prevedono la moltiplicazione tra frazioni e la semplificazione in croce. Lavora con calma, non avere fretta di finire. Non ti preoccupare se sbagli, nessuno verrà a rimproverarti.

Buon lavoro e in bocca al lupo.
Esercizi in pdf
Se vuoi puoi metterti alla prova con gli esercizi che trovi nel file pdf sotto.
![]() Moltiplicazione tra frazioni e semplificazione in croce – Esercizi.pdf
Moltiplicazione tra frazioni e semplificazione in croce – Esercizi.pdf
Buon lavoro.
A questo link della Casa Editrice Zanichelli trovi le tavole numeriche. Puoi semplicemente consultarle oppure puoi scaricarle liberamente sul tuo pc come file pdf per averle sempre a disposizione anche quando sei off-line.
Se hai domande o vuoi segnalare un errore puoi scrivere alla casella mail: matematica.facile@libero.it ; sarò grati ai lettori che segnaleranno eventuali errori presenti nell’articolo.